• 6.) Условный закон распределения составляющих

НЕПРЕРЫВНОЙ СВ.

Пусть Х,У – непрерывная СВ.

Опр.: Условной плотностью распределения составляющей Х при данном значении У=у назыв. отношение плотности распределения двумерной СВ к плотности распределения составляющей У, т.е. . f₂(x) – это плотность распределения составляющей Х.

Если известна плотность распределения системы f(x,y), то плотность распределения составляющей Х: Итак:

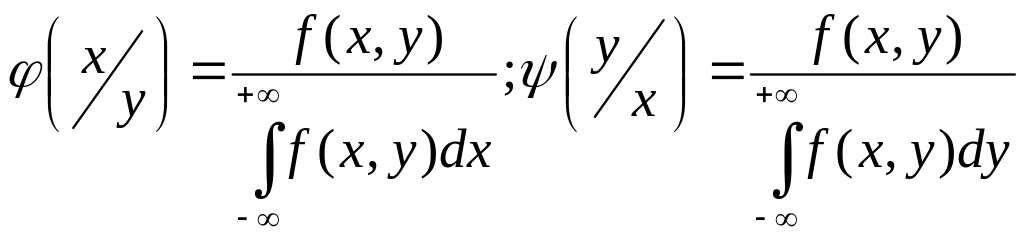
• 7.) Числовые характеристики двумерной св.

К ним относятся МО составляющих, дисперсия и средние квадратические отклонения составляющих (находятся также как и для одномерной, только через двойной интеграл).

1.) Для дискретных СВ.

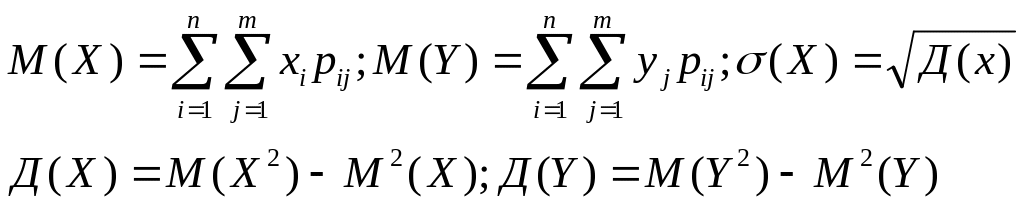
2.) Для непрерывных СВ.

f(x,y)dxdy – элемент вероятности.

• 8.) Зависимые и независимые св.

СВ Х и СВ У назыв. независимыми, если закон распределения одной из них не зависит от того какое значение приняла другая СВ.

Теорема: Необходимым и достаточным условием независимости 2-х СВ Х и У явл. условие, чтобы функция распределения системы равнялась произведению функции распределения составляющих, т.е. F(x,y)=F₁(x)*F₂(y).

(Д-во: Необходимость: Пусть Х и У – независимы, тогда Р(Х<x,Y<y)=P(X<x)*P(Y<y). Т.к. Х и У – независимы, то вероятность того, что событие X<x и Y<y произойдут одновременно равна произведению вероятностей этих событий, но Р(Х<x,Y<y) – есть F(x,y). Т.к. Р(X<x)=F₁(x); P(Y<y)=F₂(y)  F(x,y)=F₁(x)*F₂(y).

Достаточность: Пусть известно, что F(x,y)= F₁(x)*F₂(y), докажем, что Х и У – независимы. По определению F(x,y)=P(X<x,Y<y), тогда Р(X<x,Y<y)=P(X<x)*P(Y<y), но т.к. вероятность совмещения событий равна произведению вероятностей этих событий, то СВ Х и У – независимы, что и требовалось доказать.).

Следствие: Для того, чтобы СВ Х и У были независимы необходимо и достаточно, чтобы плотность распределения системы равнялась произведению плотностей вероятностей составляющих f(x,y)=f₁(x)*f₂(y).

• 9.) Корреляционный момент (ковариация).

К числовым характеристикам двумерной СВ относится и корреляционный момент.

Опр.: Корреляционным моментом двумерной СВ назыв. МО произведения отклонений этих величин. _х,у=_ху=М[(Х-М(Х))(У-М(У))].

Формула для вычисления _х,у : _ху.

_х,у=М(ХУ)-М(Х)М(У)

(Д-во: _х,у=М[ХУ-ХМ(У)-УМ(Х)+М(Х)М(У)]=М(ХУ)-М(Х)М(У)-М(У)М(Х)+

+М(Х)М(У)=М(ХУ)-М(Х)М(У) ).

Свойства: Корреляционный момент независимых СВ =0. _х,у=0, если Х и У – независ.

(Д-во: _х,у=М(ХУ)-М(Х)М(У)= [для независимых СВ М(ХУ)=М(Х)М(У) подставим] =М(Х)М(У)-М(Х)М(У)=0.

• 10.) Коэффициент корреляции.

Корреляционный момент служит для оценки тесноты связи между СВ, но он имеет размерность равную произведению размерностей СВ, т.е. его величина зависит от размерностей, что затрудняет сравнение тесноты связи между СВ, поэтому делят корреляционный момент на произведение средне квадратических отклонений и получают коэф., который не зависит от размерностей изучаемых величин.

Опр.: Коэф. корреляции двух СВ Х и У назыв. отношение корреляционного момента к произведению среднеквадратических отклонений. r_xy=_xy/(_x*_y).

Свойства: 1.) Коэф. корреляции независимых СВ =0. r_xy=0, если Х и У – независимы (обратное неверно).

2.) | r_xy|1, т.е. -1 r_xy1.

3.) Коэф. корреляции по модулю =1 только если между СВ существует линейная зависимость, т.е. У=аХ+в. | r_xy|=1

(Д-во: М(У)=М(аХ+в)=аМ(Х)+в; Д(У)=Д(аХ+в)=а²Д(Х)+0=а²Д(Х); (У)=|a|(X);

_ху=М[(Х-М(Х))(аХ+в)-аМ(Х)-в]=М[(Х-М(Х))а(Х-М(Х))]=аМ(Х-М(Х))²=аД(Х)=а_х²;

r_xy=_ху/(_х_у)=а/|а|=1, если |a|=1, то |r_xy|=1. ).

• (нет 1:) НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ НА ПЛОСКОСТИ.

Нормальным законом распределения на плоскости назыв. закон распределения СВ (Х,У) плотность вероятности которой выражаются формулой:

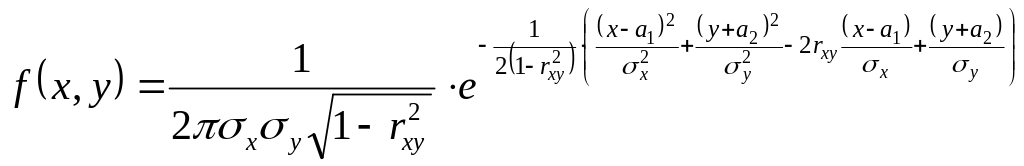, где имеется 5 параметров: а₁;а₂ – мат. ожидание М(Х) и М(У).

_х;_у – средне квадратичные отклонения. r_xy – коэф. корреляции.

Для нормального распределения равенство нулю коэф. корреляции влечет за собой независимость СВ, это не трудно проверить, если в выражение для f(x,y) подставить r_xy=0, получим f(x,y)=f₁(x)*f₂(y).