В зависимости от того, какая операция лежит в основе

измерения признака, выделяют так называемые измерительные

шкалы (были предложены С. Стивенсом в 1951 году). Эти шкалы

могут быть как метрическими (если может быть установлена

единица измерения, с которой сравнивается значение признака) и

неметрическими (единицы измерения не могут быть

установлены).

Номинативная шкала или шкала наименований. Эта шкала

является неметрической. Измерение состоит в присвоении

признаку определенного обозначения или символа. По сути –

процедура измерения состоит в классификации объектов.

Цвет глаз и волос, расса, пол

Ранговая или порядковая шкала. Также является

неметрической. Измерение в этой шкале предполагает

приписывание объектам чисел в зависимости от степени

выраженности измеряемого свойства

места на соревнованиях

Интервальная шкала. Является метрической. Измерение в

этой шкале отражает не только различия между объектами в

уровне выраженности признака (это характерно и для ранговой

шкалы), но и то, насколько больше или меньше выражен этот

признак. Равным разностям между числами в этой шкале

соответствуют равные разности в уровне выраженности

измеренного признака. Главное понятие этой шкалы – интервал,

который можно определить как долю или часть измеряемого

свойства между двумя соседними позициями на шкале. Размер

интервала – величина фиксированная и постоянная на всех

участках шкалы. Для измерения посредством шкалы интервалов

устанавливаются специальные единицы. В этой шкале нет

естественной точки отсчета (нуль условен и не означает

отсутствие измеряемого свойства).

Измерение температур

Абсолютная шкала или шкала отношений. Является

метрической. Отличие этой шкалы от предыдущей состоит в том,

что в ней устанавливается нулевая точка, соответствующая

полному отсутствию выраженности измеряемого признака.

В силу абсолютности нулевой точки мы можем сказать не

только о том, насколько больше или меньше выражено свойство,

но и о том, во сколько раз больше или меньше оно выражено.

Шкала отношений наиболее информативна, она допускает

различные математические операции и использование

разнообразных статистических методов.

Измерение температуры по кельвину

Генеральной совокупностью называют множество всех

объектов, обладающих изучаемым признаком. Число объектов

генеральной совокупности называют объемом генеральной

совокупности и обозначают N. Генеральная совокупность

определяется задачей исследования.

В подавляющем большинстве случаев генеральная

совокупность недоступна для изучения в силу следующих

причин:

 большой объем генеральной совокупности, что ведет к

трудоемким и дорогостоящим исследованиям;

 недоступность всех объектов генеральной совокупности;

 изучение объекта генеральной совокупности в ряде случаев

ведет к его разрушению.

Выборкой или выборочной совокупностью называют

множество объектов, отобранных случайным образом из

генеральной совокупности для изучения. Количество объектов в

выборке называют объемом выборки и обозначают n.

Чтобы выборка являлась хорошей моделью генеральной

совокупности, она должна быть репрезентативной (или

представительной). Это означает, что все объекты генеральной

совокупности должны иметь одинаковые шансы попасть в

выборку.

Статистическим распределением выборки называется

соответствие между вариантами i x и их частотами i n или

относительными частотами i

.Статистическое распределение выборки может быть

представлено в виде безинтервального ряда или в виде

интервального ряда.

 Безинтервальный (дискретный) ряд строится в том

случае, когда число различных вариант мало (малый объем

выборки или при большом объеме выборки мало различных

вариант).

 Интервальный ряд строится в том случае, когда

объем выборки большой, изучаемый признак непрерывен, много

различных вариант.

Статистическая гипотеза – это предположение о виде

неизвестного распределения или об его параметрах.

Статистический критерий – это случайная величина, закон

распределения которой известен в случае истинности гипотезы 0 H ,

которая служит для проверки гипотез.

Наблюдаемое значение критерия ( H K ) – это значение

критерия, вычисленное по выборке, то есть зависящее от

выборочных значений.

Допустимая область ( Д K ) – это область значений критерия,

которые не противоречат нулевой гипотезе.

Критическая область ( KP K ) – это область значений критерия,

при которых отвергается 0 H и принимается 1 H .

Критические точки ( KP k ) – это точки, отделяющие

критическую область от допустимой.

 Тип организации эксперимента – являются выборки

зависимыми или независимыми.

 Выборки называются независимыми (или несвязными), если

процедура эксперимента и результаты измерения, полученные на

одной из выборок, не оказывают влияния на особенности протекания

эксперимента и результаты измерения у другой выборки.

 Выборки называются зависимыми (или связными), если

процедура эксперимента и результаты измерения, полученные на

одной выборке, оказывают влияние на особенности протекания

эксперимента и результаты измерения у другой выборки.

Следует подчеркнуть, что если исследование проводится на

одной и той же группе, даже если при этом изучаются разные

признаки и свойства, то выборки будут зависимыми.

Использование

зависимых выборок позволяет снизить влияние случайных причин и

сгладить индивидуальные различия между исследуемыми объектами.

 Параметрические критерии основаны на конкретном виде

распределения изучаемой случайной величины (как правило, на

нормальном распределении) и используют числовые характеристики

выборочной совокупности (выборочную среднюю, выборочную

дисперсию и т.п.), которые являются точечными оценками

параметров генеральной совокупности.

 Непараметрические критерии не базируются на

предположении о виде распределения изучаемой величины и

используют непосредственно выборочные данные, а не параметры

выборки.

Если изучаемая величина распределена нормально, то отдают

предпочтение параметрическим критериям, так как они обладают

большей мощностью. Но как показывает практика, подавляющее

большинство данных в психологических исследованиях не имеет

нормального распределения, поэтому часто применяются критерии

непараметрические.

Если в результате исследования возникает предположение, что

изучаемая величина может иметь нормальное распределение, то это

предположение необходимо проверить. Для этого используются так

называемые критерии согласия.

1 Описательная статистика

1. Какие числовые характеристики относятся к мерам центральной тенденции?

средние величины - такие значения признака, вокруг которых группируются отдельные наблюдаемые значения элементов: среднее арифметическое (выборочная средняя), мода, медиана, степенные средние (среднее гармоническое, среднее геометрическое).

2. Что характеризует выборочная средняя?

Среднее арифметическое (выборочная средняя) – это средняя арифметическая всех вариант в выборке, обозначается 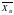и вычисляется по формуле: (для группированной выборки) или (для негруппированной выборки).

характеризует среднюю варианту признака

3. Что характеризует медиана?

Медиана (обозначается Мd или Ме) – это значение, которое делит упорядоченное множество данных пополам, так что одна половина значений оказывается больше медианы, а другая – меньше.

4. Что характеризует мода?

Мода - это такое значение признака, которое встречается наиболее часто.

5. Что такое среднее гармоническое? В каком случае применяется?

Среднее гармоническое чисел x₁, x₂, ..., x_n - число, обратная величина которого является средним арифметическим обратных величин данных чисел, т. е. число

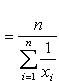или .

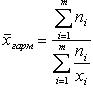Среднее гармоническое необходимо в том случае, когда наблюдения, для которых мы хотим получить среднее арифметическое, заданы обратными значениями

6. Что такое среднее геометрическое? В каком случае применяется?

Среднее геометрическое положительных чисел x₁, x₂, ..., x_n - число, равное арифметическому корню n-й степени из их произведения, т. е.

или .

Среднее геометрическое используют тогда, когда среднее значение вычисляют для значений, заданных через некоторые равные промежутки времени (рост или снижение успеваемости, заработной платы, вклада в банке за несколько лет).

Среднее геометрическое применяют тогда, когда переменная с течением времени изменяется примерно с одинаковым соотношением между измерениями.

Среднее геометрическое применяют также тогда, когда отдельные значения в статистической совокупности удалены от других значений; это меньше влияет на среднее геометрическое по сравнению со средним арифметическим, а потому дает более правильное представление о среднем.

7. Какие меры центральной тенденции можно применять в различных измерительных шкалах?

Тип шкалы	Меры центральной тенденции
Номинативная	мода
ранговая	Мода, медиана
интервальная	Мода, медиана, среднее арефметическое
Шкала отношений(абсолютная)	Мода, медиана, среднее арефметическое

8. Какие числовые характеристики относятся к мерам разброса?

К мерам разброса относят размах, квартильный размах, дисперсию, среднее квадратическое и стандартное отклонение, среднее отклонение, коэффициент вариации.

Особую группу составляют асимметрия и эксцесс. Они описывают другие свойства распределения.

9. Что такое размах выборки?

Размах просто измеряет на числовой шкале расстояние, в пределах которого изменяются оценки.

Исключающий размах – это разность максимального и минимального значений в выборке.

Включающий размах — это разность между естественной верхней границей интервала, содержащего максимальное значение, и естественной нижней границей интервала, включающего минимальное значение.

10. Что характеризует выборочная дисперсия? Чем отличается исправленная выборочная дисперсия?

Выборочная дисперсия – это средняя арифметическая квадратов отклонений вариант от выборочной средней, обозначается 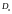и вычисляется по формуле: 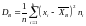(для группированной выборки) ил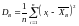и (для негруппированной выборки).

Выборочная дисперсия описывает разброс вариант относительно выборочной средней и характеризует точность измерений. Выборочная дисперсия всегда положительна

Исправленная выборочная дисперсия:

Чаще всего вычисляют сразу исправленную дисперсию по формуле:

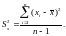
11. Что такое стандартное отклонение? Стандартная ошибка?

Среднее квадратическое отклонение – это положительное значение квадратного корня из дисперсии (обозначается _x).

Стандартное отклонение, обозначаемое s_x, определяется как положительное значение квадратного корня из дисперсии. Для определения s_x надо сначала найти , а затем вычислить квадратный корень из :

12. Что такое среднее отклонение?

Расстояние каждого x_i от 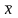определяется с помощью взятия числа по модулю. Оно равно 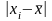. Среднее значение п расстояний оценок от их среднего называется средним отклонением, .

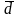13. Что такое квантиль? Квартиль? Квартильный размах?

Кванти́ль в математической статистике – такое число, что заданная случайная величина не превышает его лишь с фиксированной вероятностью.

• 0,25-квантиль называется первым (или нижним) квартилем;

• 0,5-квантиль называется медианой или вторым квартилем;

• 0,75-квантиль называется третьим (или верхним) квартилем.

Таким образом, квартили – это значения признака, делящие ранжированную совокупность на четыре равновеликие части.

Квартильный размах – это интервал, в котором вокруг медианы сосредоточилось 50% респондентов. Он равен разности значений 75-й квантили и 25-й квантили (верхней квартили и нижней квартили).