45. Необходимое условие экстремума функций двух переменных.

Функция z = f ( x, y) может иметь экстремум лишь в тех точках, в которых обе частные производные 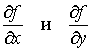обращаются в ноль или перестают существовать.    Действительно, фиксируя попеременно х = х₀ или у = у₀, получим попеременно функцию одного аргумента, для которой воспользуемся необходимым условием экстремума функции одного переменного.    Эта теорема не является достаточной, но позволяет находить точки, «подозрительные на экстремум».

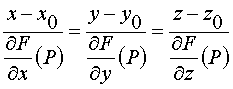;              (19)

19. – уравнение нормали, построенной в точке Р к поверхности s .

46. Достаточные условия экстремума функций двух переменных.

Пусть в некоторой области, содержащей точку М₀(х₀, у₀), функция f (x, y) имеет непрерывные частные производные до второго порядка в точке М₀(х₀, у₀) и некоторой её окрестности. Пусть, кроме того, пусть в этой точке М₀(х₀, у₀) выполняются необходимые условия экстремума функции f (x, y)

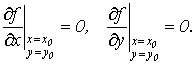(1)

Тогда функция f (x, y) в точке М₀(х₀, у₀) имеет максимум, если

В²– А·С < 0, A < 0;

функция f (x, y) в точке М₀(х₀, у₀) имеет минимум, если

В²– А·С < 0, A > 0;

функция f (x, y) в точке М₀(х₀, у₀) не имеет ни максимума, ни минимума, если

В²– А·С > 0;

функция f (x, y) в точке М₀(х₀, у₀) может иметь, и может не иметь экстремум (в этом случае требуются дополнительные исследования), если

В²– А·С = 0;

где

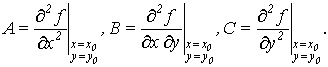
   Доказательство. Представим приращение функции по формуле Тейлора в виде

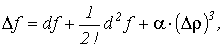(2)

где    Так как для функции f (x, y) в точке М₀(х₀, у₀) выполнены соотношения (1), то (2) можно представить в виде

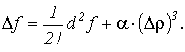(3)

Для достаточно малого Δρ знак левой части соотношения (3) будет совпадать с d² f

где 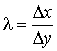, Δу ≠ 0 и обозначение sign A означает знак величины А

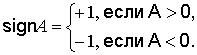
         Знакоопределённость квадратного трёхчлена, а значит определённость знака приращения функции для любых значений λ, имеет место только в одном случае - в случае отрицательного дискриминанта квадратного трехчлена В² – А С < 0. Если к тому же А < 0, то квадратный трехчлен отрицателен для любых значений λ, значит отрицательно приращение функции, что соответствует случаю локального максимума функции в данной точке.