42. Производная по направлению функций нескольких переменных.

Рассматривается функция и единичный вектор . Проводится прямая l через т.М₀ с направляющим вектором

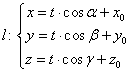
Определение 1. Производная функции u = u(x, y, z) по переменной t называется производной по направлению l

Так как на этой прямой u – сложная функция одной переменной, то производная по t равна полной производной по t (§ 12).

Она обозначается и равна

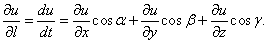
43. Градиент функции. Связь между производной по направлению и градиентом функции.

Градиентом функции u(х₁,х₂,…,х_n) называется вектор, координаты которого равны частным производным функции u :

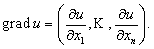
В нашем случае 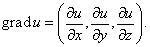Таким образом, производная по направлению равна:

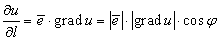, где φ − угол между направляющим вектором прямой и градиентом функции в данной точке. Отсюда следует геометрический и физический смысл градиента функции (необходимо помнить, что 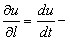скорость изменения функции вдоль прямой l ):

1.      Градиент ортогонален касательной плоскости к поверхности уровня в данной точке.

2.      Градиент направлен в сторону максимального роста (изменения) функции в т.М₀ .

{Этот максимум достигается при φ = 0, т.е. при }

3. Величина наибольшей скорости роста функции равна . Связь производной по направлению с частными производными

   Предположим теперь, что функция f (М) дифференцируема в точке М. Приращение функции f(М) в точке М вдоль прямой l можно записать в виде

.

где – бесконечно малые функции при Δ l → 0. Разделив обе части равенства на Δl и учитывая, что

,

получим

.

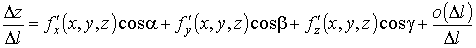Переходя к пределу в этом равенстве при Δl → 0 , получаем формулу для производной по направлению

.

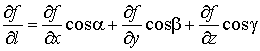Из этой формулы следует, что производная по направлению является линейной комбинацией частных производных, причем направляющие косинусы являются коэффициентами, показывающими вклад в производную по направлению от соответствующей частной производной. В частности,

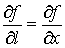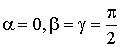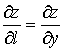при , при .

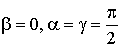   Из этого следует, что частные производные по х, у, z являются частными случаями производной по направлению осей координат.

44. Касательная плоскость и нормаль к поверхности.

Касательная плоскость и нормаль к поверхности

 Определение 1. Касательной плоскостью к поверхности в данной точке P (x₀, y₀, z₀) называется плоскость, проходящая через точку Р и содержащая в себе все касательные, построенные в точке Р ко всевозможным кривым на этой поверхности, проходящим через точку Р.

Пусть поверхность s задана уравнением F (х, у, z) = 0 и точка  P (x₀, y₀, z₀) принадлежит этой поверхности. Выберем на поверхности какую-либо кривую L, проходящую через точку Р.

Пусть х = х(t), у = у(t), z = z(t) –  параметрические уравнения линии L.

Предположим, что: 1) функция F(х, у, z) дифференцируема в точке Р и не все её частные производные в этой точке равны нулю; 2) функции  х(t), у(t), z(t) также дифференцируемы.

Поскольку кривая принадлежит поверхности s , то координаты любой точки этой кривой, будучи подставленными в уравнение поверхности, обратят его в тождество. Таким образом, справедливо тождественное равенство: F [x(t), у(t), z (t)] = 0.

Продифференцировав это тождество по переменной t, используя цепное правило, получим новое тождественное равенство, справедливое во всех точках кривой, в том числе и в точке P (x₀, y₀, z₀):

.

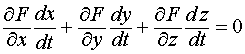Пусть точке Р соответствует значение параметра t₀, то есть x₀ = x (t₀), y₀ = y (t₀),    z₀ = z (t₀). Тогда последнее соотношение, вычисленное в точке Р, примет вид

.                  (17)

Формула (17) представляет собой скалярное произведение двух векторов. Первый из них – постоянный вектор

,

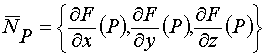не зависящий от выбора кривой на поверхности .

Второй вектор –  касательный в точке Р к линии L, а значит, зависящий от выбора линии на поверхности, то есть является переменным вектором.

П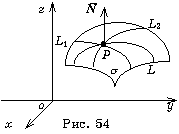 ри введённых обозначениях равенство (17) перепишем как . Его смысл таков: скалярное произведение равно нулю, следовательно, векторы и перпендикулярны. Выбирая всевозможные кривые (см. рис. 54), проходящие через точку Р на поверхности s , мы будем иметь различные касательные векторы, построенные в точке Р к этим линиям; вектор же от этого выбора не зависит и будет перпендикулярен любому из них, то есть все касательные векторы

расположены в одной плоскости, которая, по определению, является касательной к поверхности s , а точка Р в этом случае называется точкой касания. Вектор является направляющим вектором нормали к поверхности.

Определение 2. Нормалью к поверхности s в точке Р называется прямая, проходящая через точку Р и перпендикулярная к касательной плоскости, построенной в этой точке.

Мы доказали существование касательной плоскости, а, следовательно, и нормали к поверхности. Запишем их уравнения:

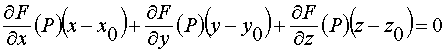;         (18)

(18) – уравнение касательной плоскости, построенной в точке P (x₀, y₀, z₀) к поверхности s , заданной уравнением F(х, у, z) = 0;