40. Производная неявной функции нескольких переменных.
Пусть непрерывная функция у от х задаётся неявно F(x, y) = 0, где F(x, y), F ' x(x, y), F ' y(x, y) есть непрерывные функции в некоторой области D, содержащей точку (х, у), координаты которой удовлетворяют соотношениям F (x, y) = 0, F ' y(x, y) ≠ 0. Тогда функция у от х имеет производную
.
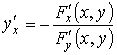Доказательство (смотри рисунок.). Пусть F ' y(x, y) > 0. Так как производная F ' y(x, y) непрерывна, то можно построить квадрат [х0 - δ' , х0 + δ' , у0 - δ' , у0 + δ' ], чтобы для всех его точек было F 'y (x, y) > 0, то есть F(x, y) является монотонной по у при фиксированном х. Таким образом, выполнены все условия теоремы существования неявной функции у = f (x), такой, что F(x, f (x)) º 0. Зададим приращение Δ х. Новому значению х + Δ х будет соответствовать у + Δ у = f (x + Δ x), такое, что эти значения удовлетворяют уравнению F (x + Δ x, y + Δ y) = 0. Очевидно, что
Δ F = F(x + Δ x, y + Δ y) − F(x, y) = 0
и в этом случае
, (7)
где
.
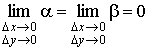Из (7) имеем
.
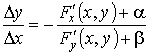Так как неявная функция у = f (x) будет непрерывна, то Δ у → 0 при Δ х → 0, значит α → 0 и β → 0. Откуда окончательно имеем
.
Что и требовалось доказать.
41. Частные производные и дифференциалы высших порядков.
Пусть
частные производные
функции
z
= f
(x,
y
), определенной в окрестности точки М,
существуют в каждой точке этой окрестности.
В этом случае частные производные
представляют собой функции двух
переменных х
и у,
определенные в указанной окрестности
точки М. Назовем их частными производными
первого порядка. В свою очередь, частные
производные по переменным х
и у
от функций
в
точке М, если они существуют, называются
частными производными второго порядка
от функции f
(М)
в этой точке и обозначаются следующими
символами
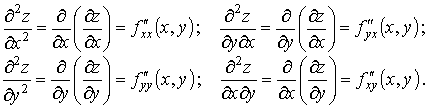
Частные
производные второго порядка вида
,
,
называются смешенными частными
производными.
Дифференциалы высших порядков
Будем рассматривать dx в выражении для dy как постоянный множитель.Тогда функция dy представляет собой функцию только аргумента x и ее дифференциал в точке x имеет вид (при рассмотрении дифференциала от dy будем использовать новые обозначения для дифференциалов):
δ (d y) = δ [f ' (x) d x] = [f ' (x) d x] ' δ x = f '' (x) d(x) δx .
Дифференциал δ (d y) от дифференциала dy в точке x, взятый при δx = dx, называется дифференциалом второго порядка функции f (x) в точке x и обозначается d2y, т.е.
d2y = f ''(x)·(dx)2.
В свою очередь, дифференциал δ(d2y) от дифференциала d2y, взятый при δx = dx, называется дифференциалом третьего порядка функции f(x) и обозначается d3y и т.д. Дифференциал δ(dn-1y) от дифференциала dn-1f, взятый при δx = dx, называется дифференциалом n - го порядка (или n - м дифференциалом) функции f(x) и обозначается dny. Докажем, что для n - го дифференциала функции справедлива формула
dny = y(n)·(dx)n, n = 1, 2, … (3.1)
При доказательстве воспользуемся методом математической индукции. Для n = 1 и n = 2 формула (3.1) доказана. Пусть она верна для дифференциалов порядка n - 1
dn−1y = y(n−1)·(dx)n−1,
и функция y(n-1)(x) дифференцируема в некоторой точке x. Тогда
Полагая δx = dx, получаем
что и требовалось доказать. Для любого n справедливо равенство
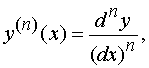или
т.е. n - я производная функции y = f ( x ) в точке x равна отношению n - го дифференциала этой функции в точке x к n - й степени дифференциала аргумента.