Связь дифференциала с частными производными

   В выражении дифференциала (2) величины А и В равны частным производным функции по соответствующим переменным:

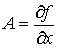  и   .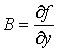

   Доказательство. Зафиксируем переменную у, так что она не получает приращения Δ y = 0. В этом случае полное приращение функции Δ z становится частным по переменной х и формула (1) принимает вид

Δ_x z = A·Δx + o(Δ x).

Откуда

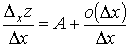. (3)

Переходя к пределу в обеих частях соотношения (3), получим

,

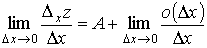откуда, в силу определения частной производной  и определения бесконечно малой более высокого порядка, чем Δ х, получим . Что и требовалось доказать.    Аналогично доказывается соотношение .    С учётом этого дифференциал (2) можно записать в виде

(4)

Из (4) следует, что дифференциалами независимых переменных х и у являются приращения этих переменных:

dx = Δ x, dy = Δ y.

Тогда дифференциал функции можно записать в виде

.

   Из определения дифференциала следует, что разность между полным приращением и дифференциалом функции в точке М есть бесконечно малая более высокого порядка, чем Δ х и Δ у:

Δ z - dz = o(Δx, Δy).

Отбрасывая при достаточно малых Δ х и Δ у величину o(Δ x, Δ y), получаем приближенную формулу Δ z » dz , из которой вытекает формула линеаризации для функции многих переменных:

.

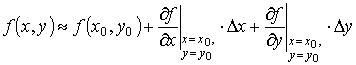Применение полного дифференциала для вычисления приближённого значения функции многих переменных

   Пример 1. Дана функция z = x² + y² – 2·x + 2·y и две точки А(1, 2) и В( 1,08; 1,94 ). Найти:

1. значение функции в точке В;

2. приближённое значение z₁ функции в точке В, заменяя приращение функции при переходе от точки А к точке В дифференциалом; оценить в процентах относительную погрешность вычисления при замене приращения функции дифференциалом.

   Решение. Вычислим значение функции в точке В:

z(B) = 1,08² + 1,94² – 2·1,08 + 2·1,94 = 6,65.

   Приближенное значение z₁ в точке В найдём по формуле линеаризации:

z₁(B) = z₀ + dz, где z₀ = z(1, 2) = 1² + 2² – 2·1 + 2·2 = 7.

Найдём приращения аргументов

Δ x = x – x₀ = 1,08 – 1 = 0,08; Δ y = y – y₀ = 1,94 - 2 = - 0,06.

Найдём значения частных производных функции в точке А

    .

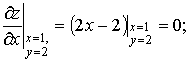
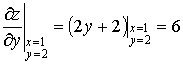Найдём значение дифференциала

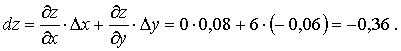
   Приближённое значение функции в точке В равно z = 7 − 0,36 = 6,64.    Относительная погрешность вычисления равна

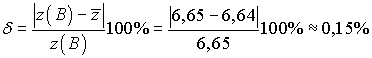
39. Производная сложной функции нескольких переменных

Пусть z = F(u, v) — некоторая функция переменных u и v. В свою очередь переменные u и v являются функциями u = φ ( x, y), v = ψ ( x, y) переменных х и у. Область изменения функций u = φ (x, y), v = ψ (x, y) принадлежит области определения функции F(u, v). Тогда z = F(φ ( x, y), ψ ( x, y) — сложная функция переменных х и у. В дальнейшем будем предполагать выполненными условия существования сложной функции.    Кроме того, пусть функции F(u, v), φ ( x, y), ψ (x, y) имеют непрерывные частные производные по своим переменным. Сохраняя переменную у постоянной, зададим переменной х приращение Δ х, тогда частное приращение переменной z определится соотношением

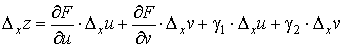(1)

где γ ₁ → 0, γ ₂ → 0 при Δ _хu → 0, Δ _хv → 0. Разделим соотношение (1) на Δ х

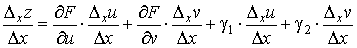(2)

Если Δ х → 0, то Δ _хu → 0, Δ _хv → 0 и γ ₁ → 0, γ ₂ → 0, поэтому, выполняя предельный переход в (2) при Δ х → 0, получим

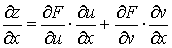(3)

   Аналогично получим

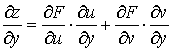. (4)