31. Формула Тейлора для многочлена. Формула Тейлора для произвольной функции. Формула Маклорена.
Если
функция
имеет
в некоторой окрестности точки
непрерывные частные производные до
(n+1)-го порядка включительно, то для любой
точки
из
этой окрестности справедлива формула
Тейлора n-го порядка:
,
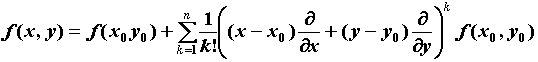
где
,
,
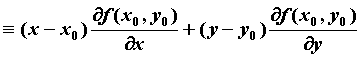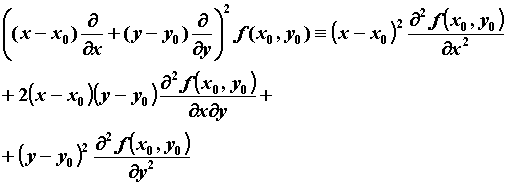
и
т.д. Формула Тейлора, записанная в
окрестности точки (0,0) называется формулой
Маклорена. Например, для функции двух
переменных при n=2:
.
ПРИМЕР 1. Разложение функции по формуле Тейлора в окрестности произвольной точки.
Аппроксимация
функции многочленом. Выражение
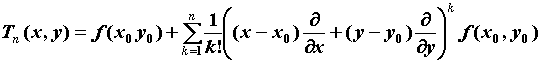называется
многочленом Тейлора n-го порядка.
Поскольку
,
то в окрестности точки функцию
можно
приближенно заменить, или, как говорят,
аппроксимировать, ее многочленом
Тейлора, т.е.
.
Чем ближе точка
к
точке
,
тем выше точность такой аппроксимации;
кроме того, точность возрастает с ростом
n. Это означает, что, чем больше непрерывных
производных имеет функция
,
тем точнее представляет ее многочлен
Тейлора.
32. Формула Маклорена для ех
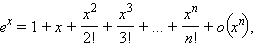
33. Формула Маклорена для sinx
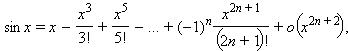
34. Формула Маклорена для cosx
35. Формула Маклорена для ln(1+x)
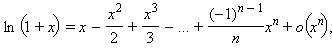
36. Формула Маклорена для (1+x)m
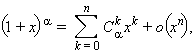где 
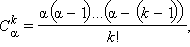
37. Понятие функции нескольких переменных. Область определения. Частные производные первого порядка и их геометрический смысл.
Величина z называется функцией переменных величин x и y на множестве D, если каждой точке этого множества соответствует одно определенное значение величины z.
Множество точек D называется областью определения функции. Обычно областью определения функции является некоторая часть плоскости, ограниченная одной или несколькими линиями.
Частными производными функции z = f(x,у) называются пределы отношения приращений функции z = z(х,у) к приращению соответствующего аргумента по направлениям ох или оу при Δх → 0 и Δу → 0 соответственно:
Частная производная по х:
при вычислении считают у = const.
Частная производная по у:
при вычислении считают x = const.
Геометрически
,
где α
– угол касательной к поверхности в
точке с направлением оси ох;
, где β – угол касательной к поверхности в точке с направлением оси оу.
38. Полный дифференциал функции двух переменных и его применение к приближённым вычислениям. Дифференциал функции
Функция z = f (M) дифференцируема в точке М, если ее полное приращение в этой точке может быть представлено в виде суммы линейной части относительно приращений аргументов и слагаемых более высокого порядка малости относительно приращений аргументов:
Δz = A Δx + B Δy + o (Δx, Δy) (1)
где
.
Определение. Дифференциалом функции z = f (M) в точке М называется линейная относительно приращений аргументов Δ x и Δ у часть полного приращения этой функции в этой точке:
d z = A·Δ x + B·Δ y. (2)