17. Емкость в цепи синусоидального тока .

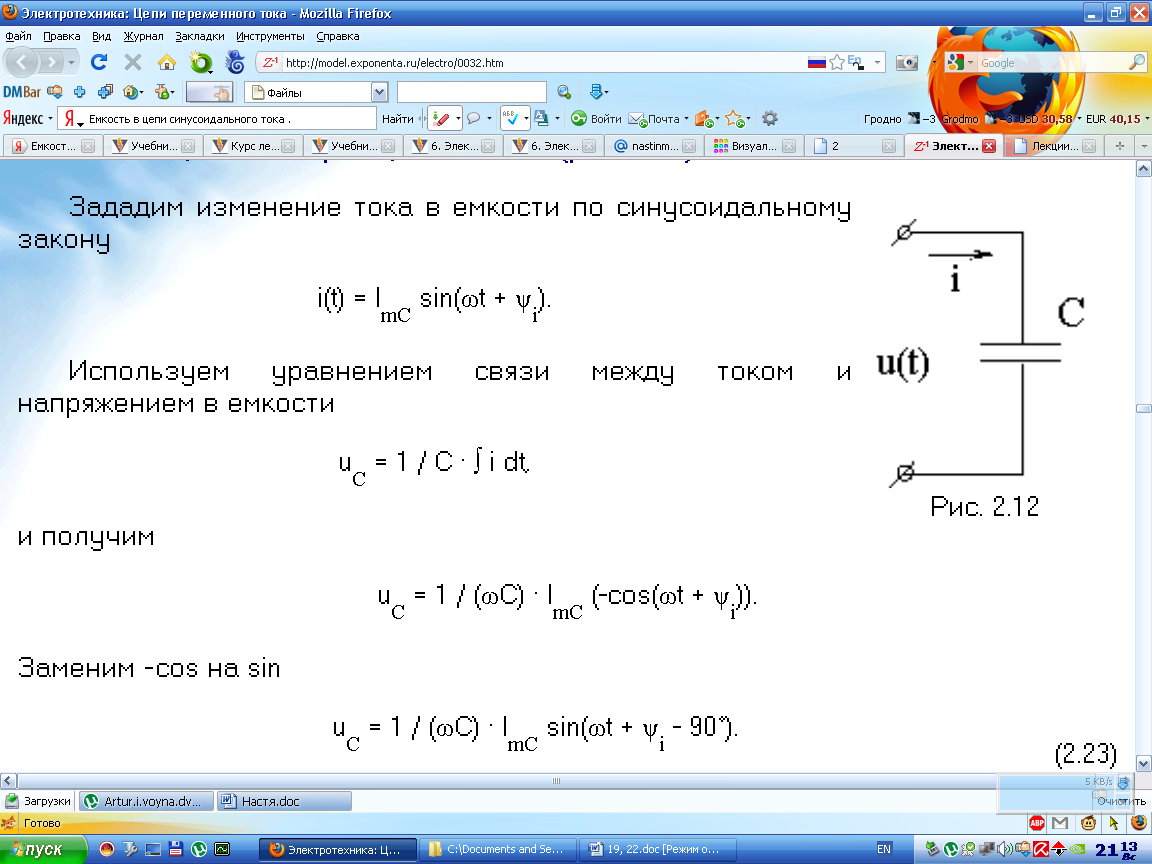  Если к конденсатору емкостью C подключить синусоидальное напряжение, то в цепи протекает синусоидальный ток:

U = U_m*sin(ωt+ψ_u);

Тогда изменяющаяся разность потенциалов будет вызывать перераспределение зарядов, и в цепи возникнет ток величина, которого будет определяться скоростью перераспределения заряда q = CU

i=dq/dt=C*du/dt=ωCU_m*cos(ωt+ψ_u)=ωCU_msin(ωt+ψ_u+π/2)

I_m = CωU_m;

ψ_i = ψ_u+π/2;

U_m = 1/cω*I_m

1/cω - емкостное сопротивление и обозначается Х_с

Сдвиг фаз φ = ψ_u - ψ_i = -π/2

I_m

U_m

Комплексное сопротивление для емкостного элемента определяется следующим образом:

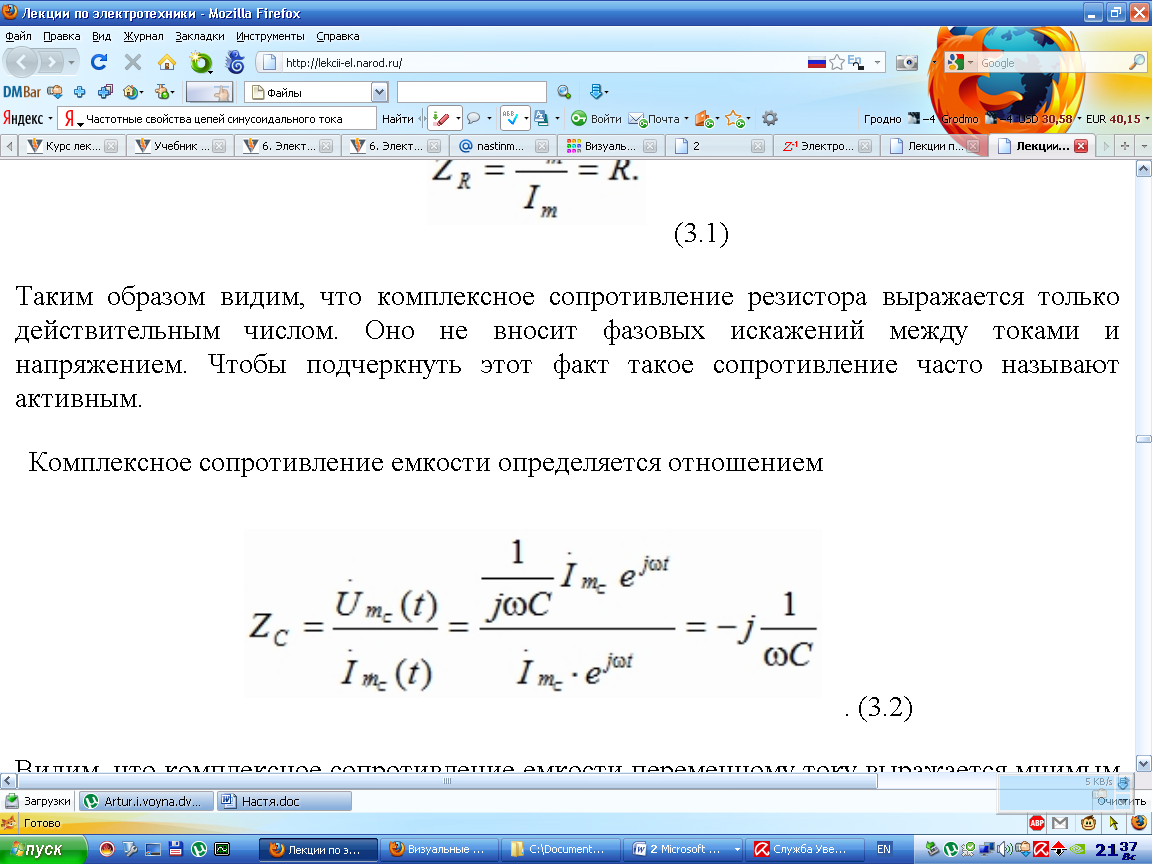
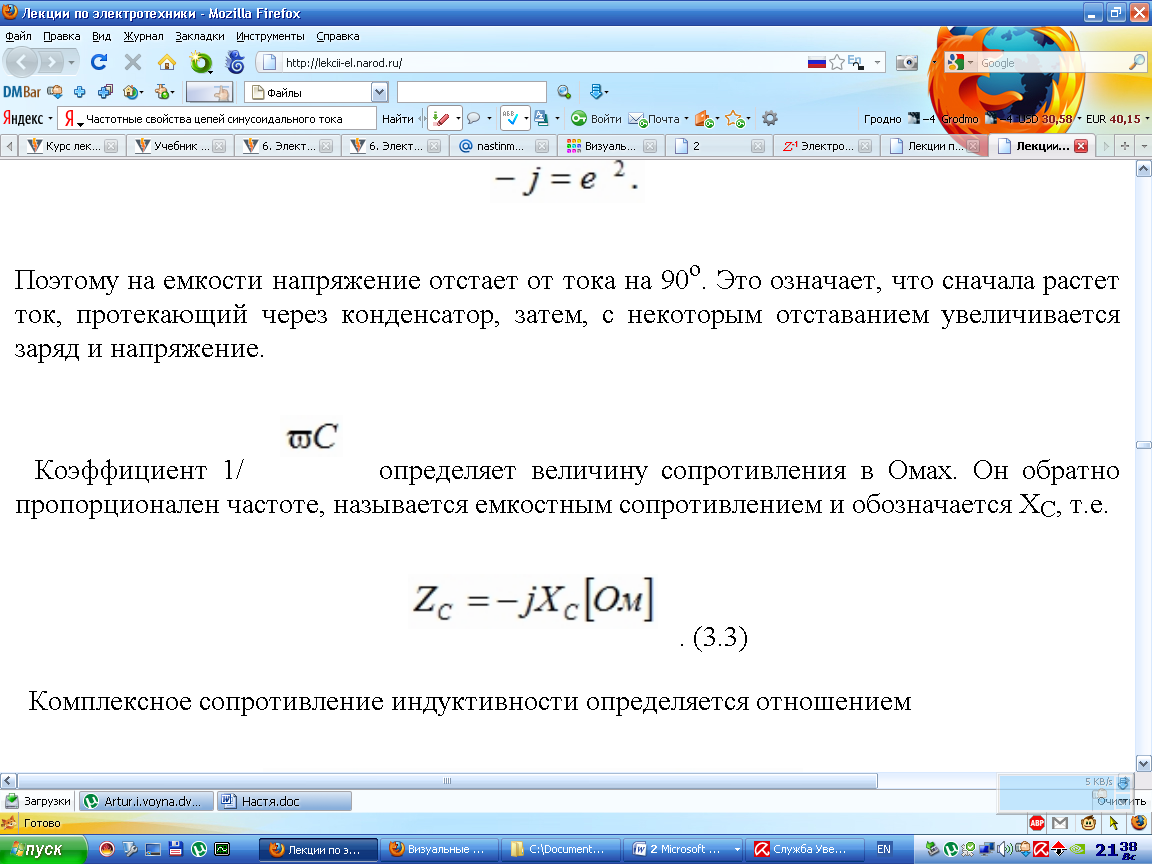
Известно, что в емкости соотношение фаз:

ψ_u = ψ_i - 90°. Для мгновенной мощности получаем

p = ui = U_m I_m · sinωt sin(ωt+π/2) = IU sin2ωt;

Первые полпериода мгновенная мощность положительна и, следовательно, емкостной элемент потребляет энергию от источника, которая запасается в электрическом поле емкостного элемента. Вторые полпериода мгновенная мощность отрицательна и это значит, что запасенная электрическая энергия в эл. поле выделяется в эл. цепь

Р = 0 - активная мощность за период.

Q_C = I² X_C [ВАР] реактивная (емкостная) мощность.

18. Последовательно соединенные элементов в цепи синусоидального тока

 Катушка с активным сопротивлением   R  и индуктивностью   L  и конденсатор емкостью  С  включены последовательно. В схеме протекает синусоидальный ток

П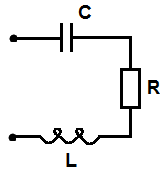 о 2-му закону Кирхгофа для мгновенного значения общее напряжение в цепи определяется как сумма мгновенных напряжений всех элементов:

U = U_R+U_C+U_L = (делаем следующую замену)

; ;

получаем =                

       Коэффициент при мнимой части комплексного сопротивления называют реактивным сопротивлением и обозначают Х= , тогда комплексное сопротивление цепи

П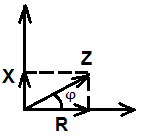 олучаем треугольник, который называют треугольником сопротивлений и из его можно определить амплитуду и начальную фазу комплексного сопротивления z= +

  ;

;

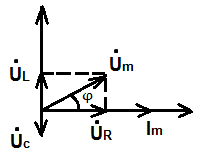
При построении векторных диаграмм цепи возник три случая.

1. X_L > X_C, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор ток.

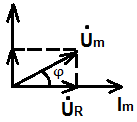U=U_R

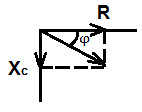
2. X_L < X_C Индуктивное сопротивление меньше емкостного. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер

3)X_L = X_C Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонансного напряжения

19. Резонанс напряжения. Векторные диаграммы.

Явление резонанса, т. е. совпадения частоты свободных колебаний ν_0, возникающих в какой-либо физической системе, с частотой вынужденных колебаний ν, сообщаемых этой системе внешними силами.

Резонанс в электрической цепи можно получить тремя способами: изменяя угловую частоту ω источника переменного тока, индуктивность L или емкость С. Различают резонанс при последовательном соединении L и С — резонанс напряжений и при параллельном их соединении — резонанс токов. Угловая частота ?0, при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура.

Резонанс напряжений. При резонансе напряжений (рис. 196, а) индуктивное сопротивление XL равно емкостному Хс и полное сопротивление Z становится равным активному сопротивлению R: Z = √( 〖R 〗^2+〖(2πνL- 1/2πνC)〗^2 ) = R

В этом случае напряжения на индуктивности UL и емкости Uc равны и находятся в противофазе (рис. 196,б), поэтому при сложении они компенсируют друг друга. Если активное сопротивление цепи R невелико, ток в цепи резко возрастает, так как реактивное сопротивление цепи X = XL—Xс становится равным нулю. При этом ток I совпадает по фазе с напряжением U и I=U/R. Резкое возрастание тока в цепи при резонансе напряжений вызывает такое же возрастание напряжений UL и Uc, причем их значения могут во много раз превышать напряжение U источника, питающего цепь.

Угловая частота ω_0, при которой имеют место условия резонанса, определяется из равенства 2πνL = 1/(2πνC).

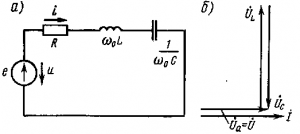
Рис. . Схема (а) и векторная диаграмма (б) электрической цепи, содержащей R, L и С, при резонансе напряжений

Отсюда имеем: ω_0= 1/√(LC )

Если плавно изменять угловую частоту ω источника, то полное сопротивление Z сначала начинает уменьшаться, достигает наименьшего значения при резонансе напряжений (при ω_0), а затем увеличивается (рис. 197, а). В соответствии с этим ток I в цепи сначала возрастает, достигает наибольшего значения при резонансе, а затем уменьшается.

Ток в резонансном режиме достигает максимума, так как полное сопротивление (z) цепи имеет минимальное значение.

I = =