1. Проверка соответствия выбранной модели распределения исходным данным (критерии согласия)

Пусть нами высказано предположение, что ряд наблюдений X₁, X₂ , … X _n образует случайную выборку, извлеченную из генеральной совокупности с некоторой модельной функцией распределения F_mod(X, ¹

, … ^s), где общий вид функции F_mod (т.е. тип модели) считается известным, а параметры, от которых она зависит, могут быть как известными, так и неизвестными.

Описываемые нами критерии согласия предназначены для проверки гипотезы:

H₀ : =

(2)

и основаны на использовании различных мер расстояний между анализируемой эмпирической функцией распределения определяемой по выборке X₁, X₂ , … X _n и гипотетической модельной F_mod(X, ¹, … ^s).

1. Критерий Пирсона.

Критерий согласия позволяет осуществлять проверку гипотезы (2) в условиях, когда значения параметров ¹, … ^s модельной функции распределения не известны исследователю. Для измерения степени отклонения эмпирического распределения от модельного этот критерий использует статистику

,где

- частота, R – общее число возможных значений или интервалов группирования, S – количество параметров распределения.

Процедура статистической проверки гипотезы (2) складывается в данном случае из следующих этапов:

1. Весь диапазон значений исследуемой случайной величины разбивается на ряд интервалов группирования , , … не обязательно одинаковой длины. Это разбиение на интервалы необходимо получить следующим условием:

1. общее количество интервалов R должно быть неменьшим 8 (Предполагается, что число s неизвестных параметров ¹, … ^s не превосходит 7 (на практике как правило s 3). Если же отказаться от этого предположения, то требование а) следовало бы заменить более жестким R

2. в каждый интервал группирования должно попасть не менее 7 – 10 выборочных значений , причем желательно, чтобы в разные интервалы попало примерно одинаковое число точек.

3. если диапозон исследуемой случайной величины - вся числовая прямая (полупрямая), то крайние интервалы группирования будут полупрямыми (соответственно один из них).

1. На основании выборочных данных X₁, X₂ , … X _n строятся статистические оценки 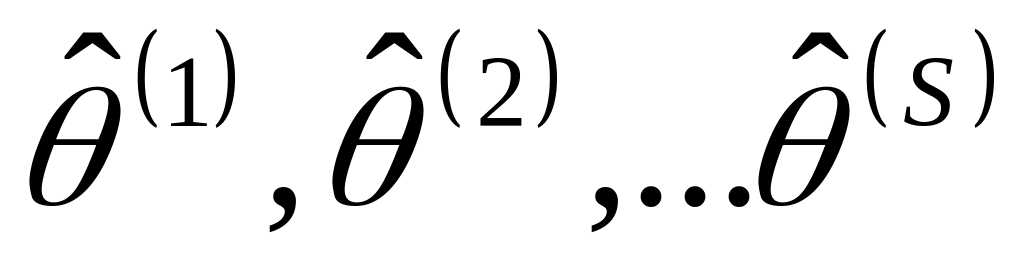неизвестных параметров , от которых зависит данный закон распределения F (гл.8). Более корректным способом действия считается тот, при котором оценки вычисляются на основе сгруппированных данных.

2. Подсчитываются числа точек, попавших в каждый из интервалов группирования и вычисляются вероятности событий 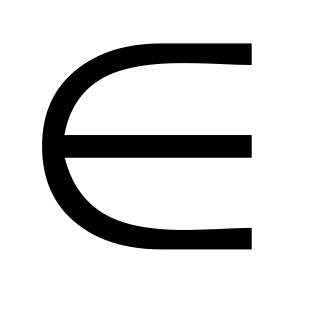, т.е. вероятности попадания в те же интервалы

3. Вычисляется величина критической статистики , доли из специальных таблиц находятся 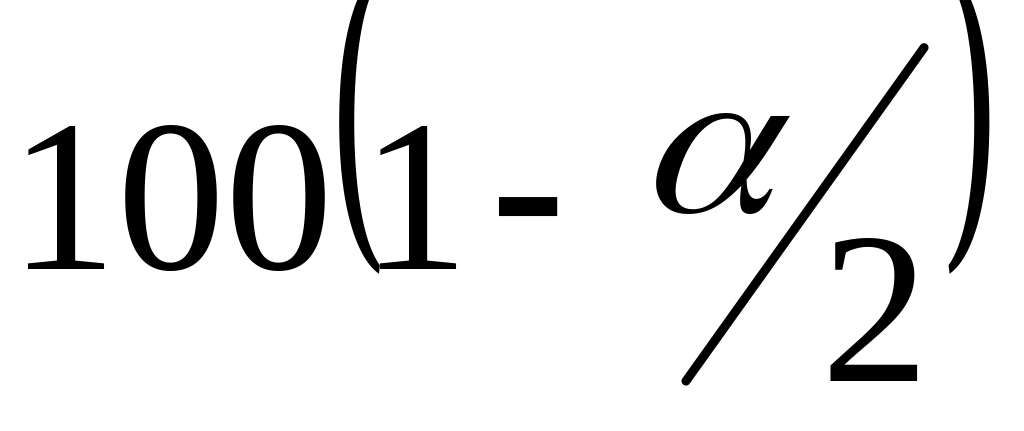% - ная точка и 100 % точка распределения с R-S-1 степенями свободы ( - уровень значимости)

Если

, то

гипотеза о том, что исследуемая случайная величина действительно подчиняется закону распределения принимается.

Выполнение неравенства