Аумалы күш. Эйлер формуласы
Сығушы күштің шамасы аумалы күшке теңелгенде арқалық орнықтылығын жоғалтпай, шамалы иіліп, талғаусыз тепе-теңдік күйде болады (7.2, а-сурет).
Ию моментінің таңбалары туралы ереже бойынша, иілген арқалықтың дөңес жағы жоғары жатса, оның қималарындағы ию
7.1-сурет
моменттері теріс, иілу мөлшерлері оң таңбалы, ал дөңес жағы төмен жатса, ию моменті оң, иілу мөлшері теріс таңбалы.
Олай болса, координаты -ке тең. арқалықтың қимасындағы ию моменті
.
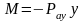(7.01)
Арқалық серпімді деформацияланады деп, серпімді сызығының, дифференциалдық тендеуін құрайық:
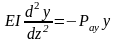немесе
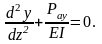(7.02)
Енді
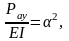(7.03)
деп белгілейік. Сонда 7.02 теңдеуін келесі түрде жазуға болады.
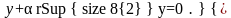(7.04
Бұл сызықты дифференциалдық. теңдеудің шешімі
Мұндағы А және В — тіректердегі келесі шарттарды қанағаттандыратын интегралдық тұрақты шамалар.
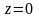болса,
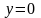,z
= l
болса,
у=0
Бірінші
шарт бойынша А=0, өйткені cos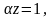
sin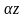
=
0. Олай
болса,
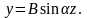(7.05)
Екінші
шарт бойынша
.
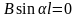Егер
= 0 болса, онда арқалықтың
кез келген қимасындағы иілу мөлшері
нөлге тең болғаны.
Бұл шешім есептің бастапкы шартына
қайшы, сондықтан
,
,
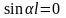яғни
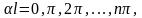осыдан
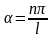немесе
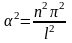(7.06)
Алынған 7.03, 7.06 теңдіктерін салыстырып
екенін
көреміз.
Сығылған
арқалық орнықтылығын ең кiшi қатаңдық
жазықтығында жоғалтады, олай болса
,
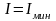яғни
.
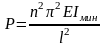(7.07)
Енді стреженьнің орнықты тепе-тендік күйінен ауытқуына сәйкес, аумалы күштің ең кіші мәнін табайық..
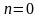болса
.
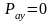Бұл
шешім есептің бастапқы шартына қайшы,
демек аумалы күш
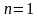болғанда өзінің ең кіші мәніне ие болады
(7.08)
Бұл формуланы 1744 жылы Петербург академиясының академигі Л.Эйлер формуласы деп атайды. Егер 7.05, 7,06 теңдеулерін бірге қарастырсақ, сығылған арқалықтың серпімді сызығы келесі теңдеумен өрнектеледі:
болса
яғни
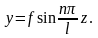(7.09)
Соңғы теңдеуден бойынша туынды алып, нөлге теңестірейік
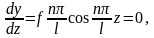мұндағы
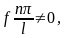олай болса,
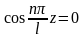
Косинустың
ең кіші мәніне сәйкес аргумент
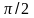болғандықтан,
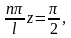осыдан
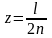(7.10)
болғанда z=l/2. Демек, талғаусыз күйдегі қос тіректі
арқалықтың серімді сызығы синусоиданың жарты толқынына сәйкес келеді, ең, үлкен иілу мөлшері ортасында жатады (7.2,а-сурет).
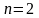болса
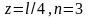болса,
.
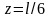Яғни,
тірек
аралығындағы
синусоидалық жарты толқындардың саны
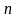-ге
тең (7.2,б, в-сурет).
20 – сұрақ
Дағдарыс кернеу. Эйлер формуласының қолдану шегі. Бойлық жүктелген стерженьнің кӛлденең қимасында тік кернеу туындайды және оның шамасы жүктеме ӛскен сайын ӛседі. Дағдарыс күшке сәйкес келетін тік кернеуді дағдарыс кернеу деп атайды
19 – сұрақ
Ясинский формуласы. Іс жүзінде, кӛптеген конструкция элементтері иілгіштігі шектік мәннен кем стержень болып келеді. Мұндай стержендерді орнықтылыққа есептеудің басқа әдісін Ф.С. Ясинский ұсынды. Алдын-ала кӛптеген зерттеулердің нәтижелерін талдап және кӛптеген материалдардың ау
мен арасындағы тәуелділікті сызбаша кескіндеп, пропорционалдық шектен үлкен дағдарыс кернеулерді анықтайтын келесі эмпирикалық формуланы қорытып шығарды
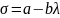
мұндағы a,b - материалдарға байланысты, тәжірибе жүзінде анықталатын,
қабылданатын тұрақты коэффициенттер. Бұл формуланы Ясин формуласы деп
атайды. Кейбір материалдар үшін, a,b коэффициенттері 2.1-кестеде берілген.