13 сұрақ

Роберт Гук 1660 жылы тәжірибе жүзінде білеудің абсолют ұзаруы (сығу жағдайында - қысқаруы) мен оған әсер етуші күштің арасында белгілі байланыс барын ашты. Ол білеудің серпімді абсолют ұзаруының білеуге әсер етуші күш пен білеу ұзындығына тура пропорционалдығын, ал қима ауданына кері пропорционалдығын және оның шамасы материалдың қасиетіне де байланыстылығын тапты. Бұл заңдылық Гук заңы деп аталады

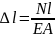
Мұндағы E - материалдың бірінші текті серпімділік модулі, ол тәжірибе жүзінде анықталады. Серпімділік модулі - материал қасиетін сипаттайтын коэффицент; ӛлшем бірлігі кернеудің ӛлшем бірлігіндей.EA – білеудің созылғандағы немесе сығылғандағы қатаңдығы деп аталады, ол материалдың созылуға немесе сығылуға қарсыласу қабілеттігін сипаттайды.

12 сұрақ

Арқалықтың әр бір қимасына әсер етуші кӛлденең күш арқалықтың бір

бӛлігін екіншісіне қарағанда, арқалықтың ӛсіне перпендикуляр бағытта

ығыстыруға ұмтылады. Сондықтан, кӛлденең күш әрбір қиманың

жазықтығында жанама кернеуді тудырады. Жанама кернеудің қостық заңына

сәйкес, осындай кернеу бейтарап ӛске параллель бағытта да әсер етеді.

Кӛлденең қиманың кез келген нүктесіндегі жанама кернеу Журавский

формуласы арқылы есептеледі:

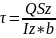
(I.2.71)

мұндағы

Q – аралықтың қарастырылып отырған қимасындағы кӛлденең күші;

Sz - кӛлденең қиманың кесілген ауданының статикалық моменті;

Iz - жоғарыда кӛрсетілген екпін моменті;

b - қарастырылып отырған нүкте жататын, бейтарап ӛске параллель,

қабаттың ені.

Кӛптеген жағдайларда арқалықты есептеуде және оның қимасын

таңдауда тік кернеу бойынша тұрғызылған беріктік шарты қолданылады.

Кейбір жағдайларда ғана жанама кернеу бойынша тұрғызылған беріктік шартты

тік кернеудің беріктік шарты бойынша жүргізілген есептеуді тексеруге

пайдаланады.

3 сұрақ

Сыртқы күштер. Материалдар кедергісі есептерін шешкенде, ең алдымен конструкция элементтеріне әсер ететін сыртқы күштің шамасы мен түсу сипатын анықтап алу қажет. Белгілідей, сыртқы күш деп денелердің бір- бірімен әсерін, демек, сол конструкция элементтерінің ӛзара әсерін де айтады. Сол сияқты берілген конструкция элементінің басқа денемен әсері қарастырылған элемент үшін, сыртқы күш болып табылады. Мысалы, шамға құйылған жермайдың салмағы шан орнатылған тұғырға түседі, одан тұғырдың аяқтары арқылы іргетасқа түседі. Элементтің ӛз салмағы да сыртқы күшке жатады. Сыртқы күштер көлемдік және беттік болып бӛлінеді. Беті арқылы берілетін сыртқы күш беттік, ал кӛлемі арқылы берілетін сыртқы күш көлемдік күш деп аталады. Беттік күштер қадалған немесе таралған күш болуы мүмкін. Қадалған күш деп, конструкция элементтеріне ӛз ӛлшемдерімен салыстырғанда ӛте шағын аудан арқылы берілетін күшті айтады. Қадалған күштің ӛлшем бірлігі ньютон (Н), килоньютон (кН), меганьютон (МН). Мысалы, тісті берілістегі тістердің бір-біріне әсері. Ауданның ӛте шағындығына байланысты қадалған күш әдетте денеге нүкте арқылы беріледі деп есептелінеді. Таралған күш деп не элементтің барлық кӛлеміне (көлемдік күш), не белгілі бір ауданына (жазықтық күш), не белгілі бір ұзындыққа (сызықтық немесе бойлық жүк) үздіксіз түсірілген күшті айтады. Ол қарқындылығымен сипатталады. Қарқындылық деп күштің бірлік кӛлемге немесе бірлік ауданға немесе бірлік ұзындыққа түсірілген шамасын айтады. Қарқындылық латынша q әрпімен белгіленеді, сәйкесінше таралған күштердің ӛлшем бірлігі: кӛлемдік күш - ; жазықтық күш - ; , ; сызықтық немесе бойлық күш - ; , . 3 3 3 м /МН, м /кН, м /Н2 м /Н2 м /кН2 м /МНм/Нм/кНм/МН

Бұл күштер таралу заңдылықтарына байланысты біркелкі таралған тұрақты және бірқалыпсыз таралған айнымалы күштер деп жіктеледі. Біркелкі таралған тұрақты күштің кез келген нүктедегі қарқындылығы ӛзара тең, ал бірқалыпсыз таралған айнымалы күштің қарқындылығы әр түрлі. Денеге тұтас кӛлемі арқылы берілетін күштер қатаң түрде үздіксіз біркелкі тараған деп қарастырылады. Кӛлемдік күшке мысал ретінде дененің салмағын, жазықтық күшке – будың қазан қабырғасына қысымын, сызықтық күшке – ені ұзындығынан ӛте аз арқалыққа ұзына бойлы түсірілген күшті келтіруге болады. Сыртқы күш әсер ететін уақытына байланысты да екі топқа бӛлінеді: тұрақты күш және уақытша күш. Тұрақты күш деп мӛлшері мен бағыты ӛзгермейтін күшті айтады. Егер денеге түскен күштердің шамасы немесе бағыты уақытқа байланысты ӛзгеріп отырса, ондай күштерді айнымалы күштер деп атайды. Сыртқы күштерді статикалық және динамикалық күштер деп те топтастыруға болады. Статикалық күш деп ӛзінің шамасын немесе түсу нүктесін баяу жылдамдықпен ӛзгертетін, осы жағдайда туындауы мүмкін үдеуді ескермеуге болатын күшті атайды. Мұндай күш әсерінен конструкцияның және оның элементтерінің тербелісі мардымсыз аз болады. Динамикалық күш деп уақытқа байланысты үлкен жылдамдықпен ӛзгеретін күшті айтады. Мұндай күштің әсерінен конструкция немесе оның элементтері елеулі тербелістерге ұшырайды. Тербеліс жылдамдығының ӛзгеруіне байланысты конструкцияда пайда болатын, оның массасы мен үдеуінің кӛбейтіндісіне тура пропорционал екпін күші шамасы жағынан конструкцияда тербеліс тудырушы сыртқы күштің шамасынан бірнеше есе үлкен болуы мүмкін. Динамикалық күштер соққы, айнымалы–қайталанбалы және т. б. түрлерге жіктеледі. Соққы күш деп кинетикалық энергиясы бар қозғалыстағы дененің екінші бір денеге соқтығысуы арқылы берілетін күшті айтады. Айнымалы–қайталанбалы күштер деп машина бӛлшектеріне уақытқа тәуелді, периодты түрде қайталанып түсетін күштерді атайды. Мысалы, қозғалыстағы машинаның шатун, білік сияқты бӛліктеріне немесе темір жол вагонының ӛсіне түсетін күштер айнымалы – қайталанбалы күштерге жатады. Жалпы жағдайда күш уақытқа тәуелді күрделі заңдылықпен ӛзгеруі мүмкін.

4 – сұрақ

Ішкі күштер. Қию әдісі. Жоғарыда айтылғандай, сыртқы күш әсерінен денелер деформацияланады. Денелердің атомнан тұратыны, ал атомдар ӛзара атомдық күшпен байланысып тепе – теңдік күйде болатыны физика курсынан мәлім. Дене деформацияланған кезде атомдардың ара қашықтығы ӛзгереді. Осының салдарынан атомдық күш қандай да бір қосымша әсерлесу күшіне – серпімді күшке ӛзгереді. Қосымша күш атомдарды алғашқы күйіне келтіруге тырысады. Бұл атомдардың қосымша ӛзара әсерлесу күші материалдар кедергісі ғылымында ішкі күш деп аталады. Ол конструкция элементтерінің сыртқы күш әсеріне қарсыласу қабілеттігін кӛрсетеді. Сонымен, ішкі күштің ӛзгеру мӛлшері, сыртқы күштің ӛзгеру мӛлшерімен тең болғанда ғана, конструкция элементтері жұмыс істеу қабілеті мен тепе–теңдік күйін сақтай алады.

Сыртқы күштердің ұлғайуымен ішкі күштердің де ӛсетіні, әрине, айқын. Бірақ ішкі күштердің шексіз ұлғайуы мүмкін емес, қандай да бір мезетте белгісіз бір нүктенің тӛңірегінде сыртқы күштерді теңестіре алмауы мүмкін. Бұл күштердің ӛзара теңсіздігі конструкцияның қирап сынуына немесе орнықтылығын жоғалтуына әкеліп соқтыратыны мәлім. Сондықтан да, ішкі күштің шамасын білмей, машиналар мен конструкциялардың беріктігін бағалау мүмкін емес.

Ішкі күштерді табу үшін, қию әдісі қолданылады. Бұл әдіс «Дене тепе–теңдік күйде тұрса, онда оның кез келген бӛлігі де тепе–теңдік күйде болады» деген механика заңдылығына негізделген. Қию әдісінің маңызы мынада. Білеу пішінді, қандай да бір денені қарастырайық. Оған теңестірілген

2 сұрақ

Сонымен, «Материалдар кедергісі» деп машина мен конструкциялардың бөліктерінің беріктігі, қатаңдығы және орнықтылығы туралы ғылымды айтамыз.

Беріктік деп конструкцияның немесе оның жеке элементтерінің сыртқы күш әсеріне қирамай қарсыласу қабілетін айтады.

Қатаңдық деп конструкция мен оның элементтерінің деформацияға қарсыласу қабілетін атайды.

Орнықтылық деп конструкцияның немесе оның элементтерінің белгілі алғашқы серпімді тепе-теңдік күйін сақтау қабілетін айтады. Есептеу денелерінің түрлері. Инженерлік практикада кездесетін сан алуан конструкция элементтері пішіндері мен ӛлшемдеріне байланысты жинақталып, тӛмендегідей қарапайым түрлерге жіктелген: 1 Білеу (брус) - екі ӛлшемі үшін,шісінен әлдеқайда кіші дене (I.2.1, а, b - сурет). Дербес жағдайда білеудің кӛлденең қимасының ауданы тұрақты, ал ӛсі түзу сызықты болуы мүмкін (I.2,1, b - сурет).

Ӛсі түзу сызықты білеуді стержень деп атайды. Білеудің өсі дегеніміз кӛлденең қималардың ауырлық центрлерінің геометриялық орны (I.2.1, c - сурет). 2 Пластина – ара қашықтығы басқа ӛлшемдеріне қарағанда ӛте кіші, екі жазық бетпен шектелген дене (I.2.2, а - сурет). 3 Қабықша - ара қашықтығы басқа ӛлшемдеріне қарағанда әлдеқайда кіші болатын екі қисық сызықты беттермен шектелген дене (I.2.2, b - сурет).

4 Массив - үш ӛлшемдері ӛзара шамалас дене (I.2.2, с - сурет). «Материалдар кедергісі» пәнінде қатаңдығы жеткілікті, аз деформацияланатын, кӛбінесе кӛлденең қималары тұрақты, білеу тәріздес жұмыр денелер немесе олардан құрылған қарапайым жүйелер қарастырылады.

10 сұрақ

Материалдардың механикалық қасиеттерін тәжірибелік зерттеу. Материалдардың сыртқы күш әсеріне қарсыласу қабілеті мен деформациялануы немесе қирауы олардың механикалық қасиеттеріне тікелей байланысты. Материалдардың механикалық қасиеттері тәжірибе жүзінде арнайы үлгілерді сынау арқылы анықталады. Үлгіні жүктеудің түрлеріне, байланысты сынау статикалық, динамикалық, циклды сынау деп, ал үлгінің деформациялану ерекшеліктеріне байланысты созуға, сығуға, июге, бұрауға сынау деп т.б. кӛптеген түрлерге бӛлінеді. Жеке жағдайларда үлгілер бұралып иілу, бұралып сығу сияқты күрделі деформацияларға сыналады. Сынау нәтижесінде алынатын механикалық сипаттамалар материалдардың жұмыс істеу шарттарына, температураға, қоршаған ортаға, күш әсерінің ӛзгеруі жылдамдығына т. б. факторларға байланысты ӛзгеріп тұрады. Сондықтан материалдардың механикалық қасиеттерін ӛзара салыстыру үшін оларды қатаң түрде бірдей жағдайларда сынайды.

Сынама үлгілердің формалары мен ӛлшемдері, оларды сынау шарттары мемлекеттік стандартта қарастырылып бекітілген.

Созу диаграммалары. Сан алуан сынау тәсілдерінің ішінде кең тарағаны – материал үлгілерін созуға сынау. Ӛйткені, созуға сынау нәтижесінде алынатын механикалык шамалар, материалдардың сыртқы күшке қарсыласу қабілетін, деформациялануын немесе қирау ерекшеліктерін айтарлықтай толық сипаттайды.

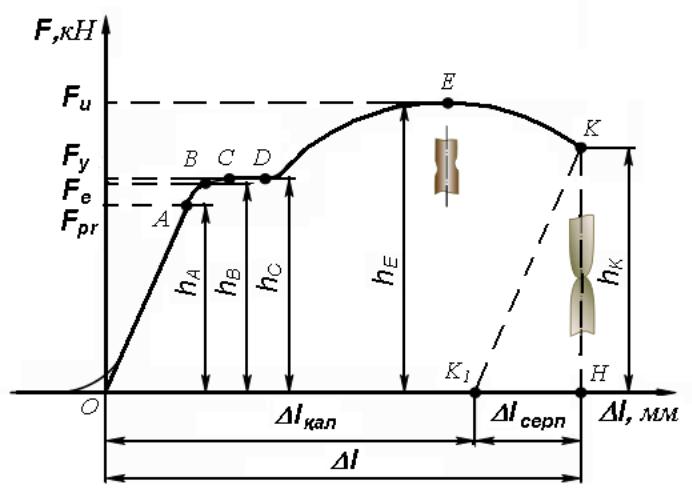
6 – сұрақ

Созылған (сығылған) білеуді беріктікке есептеу. Машиналар мен құрылымдарды және олардың элементтерін жобалағанда, негізінен келесідей үш есептің түрлерімен кездесуге болады: 1) Жобалау есебі, яғни берілген күштердің шамасына сәйкес, таңдап алынған материалдан жасалынатын конструкция элементінің беріктігін, қатаңдығы мен жеткілікті тӛзімділігін қамтамасыз ететін қиманың ең аз ӛлшемдерін анықтау. 2) Беріктікті тексеру есебі, яғни белгілі күштердің шамасы мен конструкция элементтерінің кӛлденең қима ӛдшемдері бойынша элементтердегі нақтылы кернеулердің ең үлкен шамасын анықтап, мүмкіндік кернеумен салыстыру. 3) Жүк кӛтеру қабілетін анықтау есебі, яғни белгілі конструкция элементтерінің кӛлденең қима ӛлшемдері мен материалдарының мүмкіндік кернеуі бойынша конструкция элементтерінің жүк кӛтеру қабілетін анықтау. Созылу мен сығылу деформацияның беріктік шарты келесі формуламен өрнектеледі.

Созылу деформациясымен шынжырларды, арқандарды, болттарды, әр

түрлі аспаларды есептеуде кездессек, сығылу деформациясы іргетастар мен

тіректерді есептеуде қарастырылады.

Білеуге әсер етуші күштерді созушы күштер деп қарастырсақ, (I.2.8, b -

сурет) онда білеудің ұзындығы

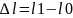(I.2.6)

шамасына ұзарады (созылады), ал ені

b b₁ b₀ (I.2.7)

шамасына қысқарады (сығылады).

Білеудің бастапқы ұзындығының ұзару шамасын - абсолют ұзару, ал

енінің қысқару шамасын b - абсолют қысқару деп атаймыз.

немесе b шамалары бойынша білеудің деформациялану қабілетін

сипаттауға болмайды, ӛйткені абсолют ұзару мен қысқару білеуге әсер етуші күшпен қатар білеудің бастапқы ӛлшем бірліктеріне байланысты. Сондықтан созылған немесе сығылған білеудің деформациялану шамасын сипаттау үшін, абсолют ұзарудың білеудің алғашқы ұзындығына, ал абсолют қысқарудың білеудің алғашқы еніне қатынастарын алған дұрыс, яғни

мұндағы E- бойлық салыстырмалы деформациясы деп, ал E’- ендік салыстырмалы деформация деп аталады. формулаларынан E мен E’ ӛлшем бірліксіз шамалар екенін кӛреміз

1 – сұрақ

Деформациялар. Қандай дене болмасын сыртқы күш әсерінен ӛздерінің ӛлшемдері мен пішіндерін ӛзгертеді, яғни деформацияланады, ақырында күштің бір жеткілікті үлкен шамасында қирайды, бірнеше бӛлшектерге бӛлінеді. Денелердің ӛлшемдері мен пішіндерінің ӛзгеруін деформация деп атайды. Ол материалдың атомдарының ара қашықтықтарының ӛзгеруі мен атом блоктарының орын ауыстыруы салдарынан туындайды.

Сыртқы күш әсері жойылғанда, денедегі деформация да жойылса, ондай деформацияны серпімді деформация деп атайды, ал дененің күш әсері

ДЕФОРМАЦИЯ МЕН ОРЫН АУЫСТЫРУ

Қандай дене болмасын сыртқы күш әсерінен өздерінің өлшемдері мен формаларын өзгертеді, деформацияланады.

Дененің сызықты өлшемдерінің өзгеруі сызықтық деформация, ал бұрыштық өлшемдерінің өзгеруі бұрыштық деформация делінеді.

Деформация нәтижесінде дененің сызықтық өлшемінің өcyi – созылу (ұзару), ал кемуі – сығылу (қысқару) деп аталады.

Деформация материалдың атомдарының ара қашықтықтарының өзгеруі мен атом блоктарының орын ауыстыруы салдарынан туады. Оның табиғатын толық зерттеп білу үшін, жазық дененің кез келген нүктесінің жанынан өзара перпендикуляр АВ, СA түзулерін алайық (I. 3, а-сурет).

Дене деформацияланғанда АС түзу сызығы шамасына ұзарады (I. 3, б-сурет). Оның орташа сызықтық салыстырмалы деформациясы келесі формуламен анықталады.

(1.01)

1.3-сурет

Б ұл қатынастың бөліміндегі АС кесіндісінің ұзындығы нөлге ұмтылғандағы шегі, А нүктесіндегі толық салыстырмалы деформацияны аныктайды

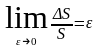. (1.02)

Енді бұрыштық деформацияны қарастырайық. Деформацияға дейінгі ВАС тікбұрышы мен деформациядан кейінгі В'А'С сүйір бұрышының арасындағы айырма берілген нүктенің бұрыштық деформациясын сипаттайды.

Сонымен күш түскен дененің кез келген нүктедегі деформациясы сызықтық салыстырмалы және бұрыштық деформациялармен сипатталады. Денеде пайда болған сызықтық және бұрыштық деформациялар сырттан әсер етуші күш жойылғанда толық жойылуы немесе жойылмауы да мұмкін. Сыртқы күш әсері жойылғанда, денедегі деформация да жойылса, ондай деформацияны серпімді деп, ал деформация толық жойылмай қалса, онда қалдық деформацияны пластикалық деформация деп атайды. Егер дененің бекіту шарттары мен нүктелеріндегі деформацияның шамасы белгілі болса, онда кез келген нүктенің деформациядан кейінгі орнын, яғни орын ауыстыру шамасын анықтауға болады. Машина бөлшектері серпімді деформацияланғанда ғана, олардың жұмыс істеу қабілеті қамтамасыз етіледі. Сондықтан, нүктелердің ең үлкен орын ауыстыру шамасы белгілі бip мүмкіндік шамадан аспауы керек. Мұндай шарт теңсіздік ретінде көрсетіліп, қатаңдық шарты деп аталады.

7 – сұрақ

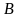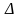
І шкі күштер дененің бір бөлігімен екінші бөлігіне көлденең қима арқылы үздіксіз жайыла таралып беріледі Олардың әсер ету заңдылығын білу үшін қима бетінде жатқан нүктесін қарастырайық (1.5, а-сурет). Нүктені қоршаған шексіз кіші ауданды , ал ол ауданға сәйкес келетін ішкі күшті деп белгілейік. Ішкі күш ның шексіз кіші аудан 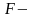ке қатынасы

1.5-сурет

нүктесіндегі ішкі күштің орташа шамасын – орташа кернеуді аңықтайды.

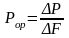. (1.04)

Шексіз кіші аудан нөлге ұмтылғандағы көрсетілген қатынастың шегі В нүктесіндегі толық кернеу деп аталады:

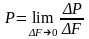. (1.05)

Толық кернеудің көлденең қима жазықтығына перпендикуляр OZ өсте, түсіріген проекциясы тік кернеу деп аталып, OZ әрпімен белгіленеді, ал қима бетіне түcipiлгeн проекциясы жанама кернеу деп

1.6-сурет

а талып, әрпімен белгіленеді (1.5, б-сурет).

Суреттен, толық кернеу 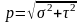, екендігін көреміз.

8 – сұрақ

Параллель өстерге қарағанда инерция моментерінің арасындағы тәуелділік

Қиманың өзара перпендикуляр X, У центрлік өстеріне қарағандағы

4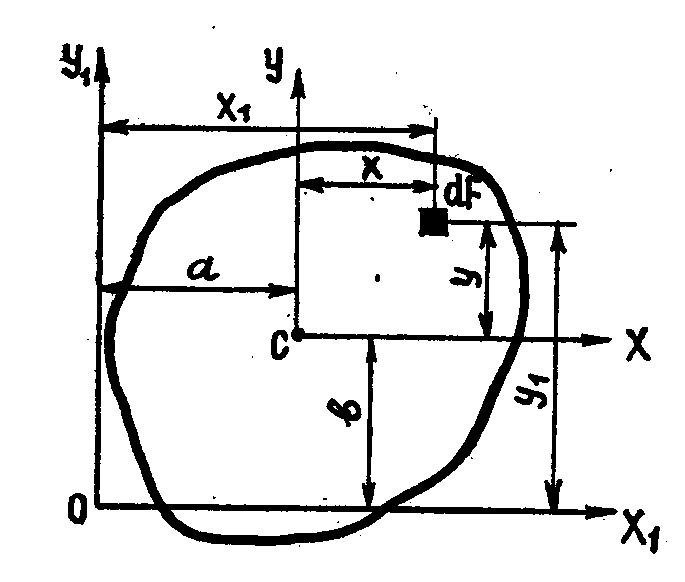 .4-сурет

инерция моменттері белгілі дейік. Енді осы өстерге параллель жаңа 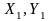өстеріне қарағандағы инерция моменттерінің шамаларын анықтайық (5.4-сурет). Бөлініп алынған тің ХОУ жүйесіндегі координаттары х, у, ал жүйесіндегі координаттары 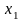= x+a, 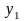=y+b болсын.

Фигураның 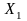және 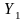өстеріне қарағандағы инерция моменттері төмендегі интегралдар мен анықталады

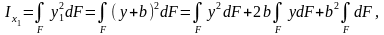
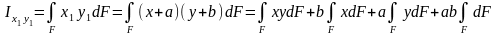
Бұл өрнектердегі 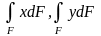интегралдары, центрлік Х, У

өстеріне қарағандағы статикалық моменттер болғандықтан нөлге тең, олай болса:

. (5.06)

С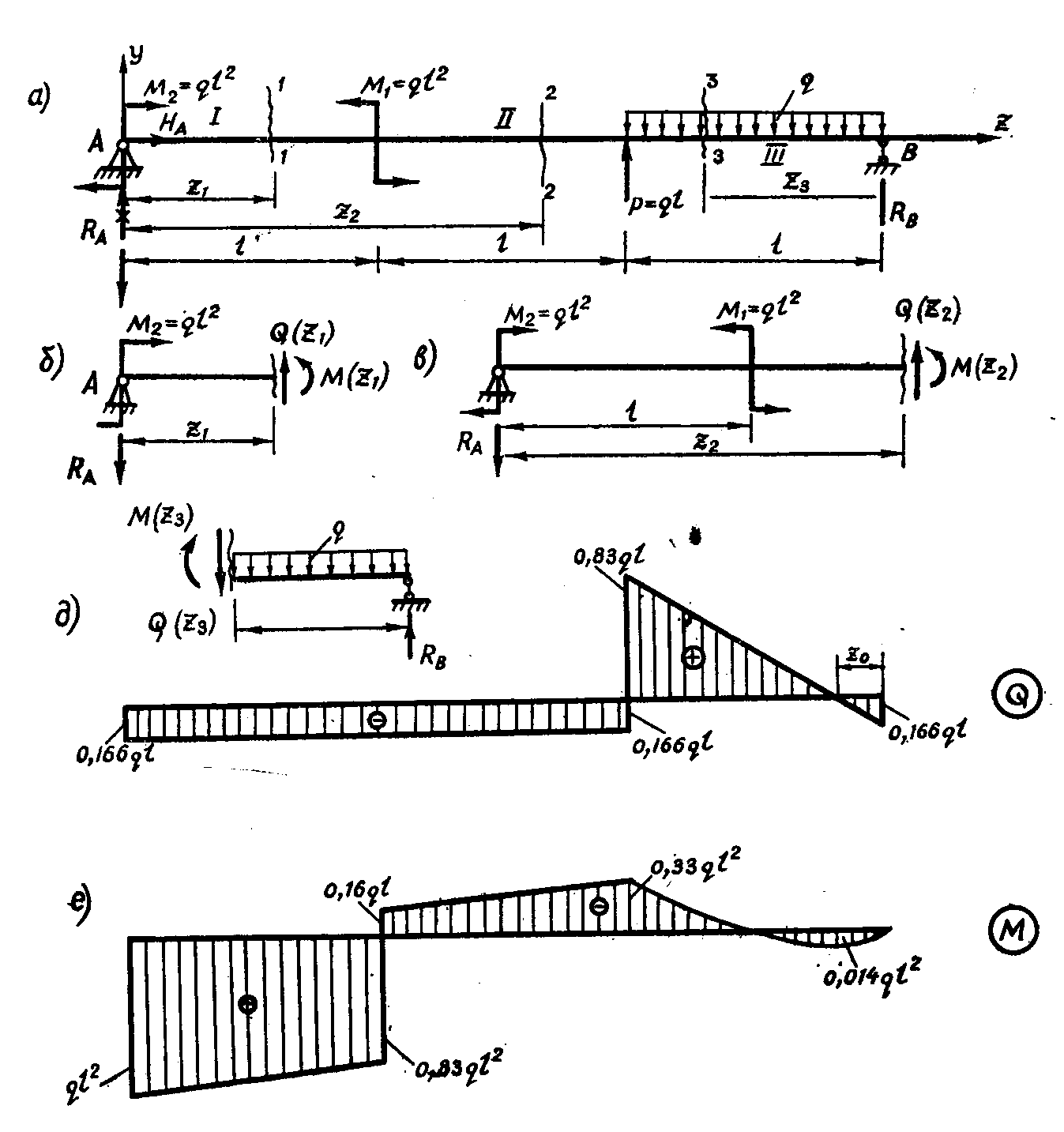 онымен, фигураның кез келген центрлік өсіне параллель өске қарағандағы өстік инерция моменті, центрлік өстік инерция моментіне, фигураның ауданын осы өстердің ара қашықтығының квадратына көбейтіп қосқанға тең. Центрлік өске қарағандағы өстік инерция моменті, осы өске параллель, кез келген өске қарағандағы өстік инерция моменттерінен кіші.

Фигураның өзара перпендикуляр центрлік өстеріне параллель өстерге қарағандағы центрден тепкіш инерция моменті, фигура ауданының осы өстердің ара қашықтықтарына көбейтіп қосқанға тең (5.4-сурет).

Жалпы жағдайда, күрделі фигуралардың инерция моменттері келесі формулалармен анықталады

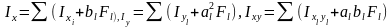(5.07)

15 – сұрақ

Бұрылған өстерге қарағандағы инерция моменттерінің арасындағы байланыс

Қиманың ауырлық центрі арқылы өтетін өзара, перпендикуляр X, У өстеріне қарағандағы инерция моментері белгілі болсын (5.5-сурет).

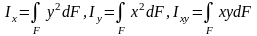
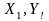Енді қиманың осы өстерге бұрышын жасайтын центрлік өстеріне қарағандағы инерция моменттерін табайық (өстердің сағат тіліне қарсы бағытта бұрылуы оң деп қабылданған).

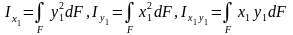
4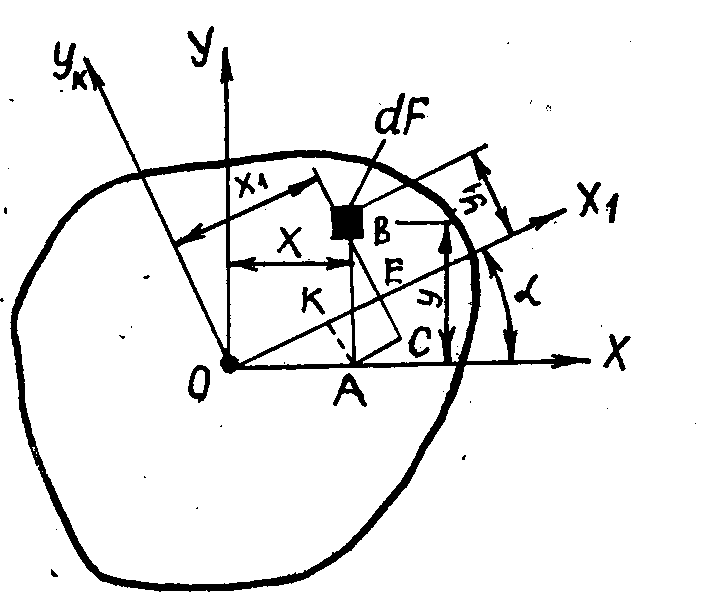 .5-сурет

Ол үшін 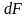-тің берілген ХО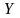 жүйеciндeгi координаттары мен жаңа Х₁ОУ₁ жүйесіндегі координаттарының арасындағы өзара байланысты анықтайық

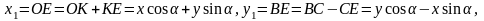Олай болса

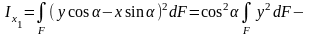
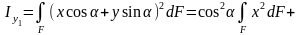
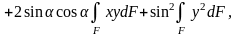
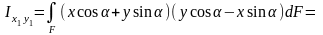
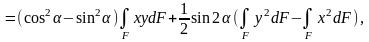
(5.08)

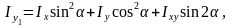(5.09)

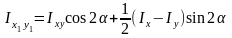(5.10)

Алынған 5.08 және 5.09 өрнектерін қоссақ 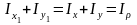екенін көреміз.

Яғни, өзара перпендикуляр өстерге қарағандағы инерция моменттерінің қосындысы, осы өстерді кез келген біp бұрышқа бұрғаннан өзгермей, тұрақты болып қалады.

Енді, өстік инерция моменттерінің айырмасын қарастырсақ

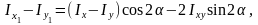
өзара перпендикуляр өстерге қарағандағы өстік инерция моменттерінің айырмасы, осы өстерге қарағандағы центрден тепкіш инерция моментінің шамасына тең екенін көреміз.

11 – сұрақ

Инерцияның бас өctepi, бас momehttepi

Алдыңғы параграфта алынған 5.08, 5.09, 5.10 формулаларына қарап инерция моменттерінің тек бұрышына (5.5-сурет) тәуелді екенін байқауға болады. Олай болса, өстің инерция моменттерінің экстремальді, мәндеріне сәйкес бұрышының мәнін анықтауға болады. Ол үшін 5.08 немесе 5.09 өрнегінен біp рет туынды алып, оны нөлге теңестірсек болғаны.

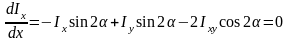
осыдан

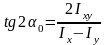(5.11)

Алынған формула бойынша бұрышының екі мәні бар: біpі ao екіншісі 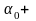90°; демек инерция моменттерінің мәні экстремальды өзара перпендикуляр екі-ақ өс бар. Бұл өстер бас өстер деп аталады, оларға қарағандағы өстік инерция моменттері бас инерция моменттері деп аталады. Бас өстерге қарағандағы центрден тепкіш инерция моменті нөлге тең.

Енді 5.08 және 5.09 өрнектеріндегі -нің орнына қойып, бас инерция моменттерің анықтаймыз (5.5-сурет).

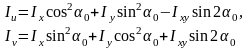
Өрнектерді тригонометриялық функциялардан босатып басты инерция моментерінің формулаларын келесі түрге келтіруге болады

. (5.12)

Өстік инерция моменті мен қима ауданының арасындағы байланыс арқылы табылатын шаманы

,

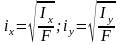қиманың инерция радиусы деп атайды.

Жарты өстері бас инерция радиустеріне тең (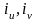 ), бас өстерге тұрғызылған эллипс – инерция эллипсі деп аталады, келесі теңдеумен өрнектеледі

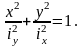
Инерция эллипсінен кез келген центрлік өске карағандағы инерция моментін табуға болады. Мысалы, X_i өсіне қарағандағы инерция моментін табу үшін, осы өске параллель эллипске жанама жүргізіледі. Эллипс центрінен жанамаға түсірілген перпендикулярдың (СА) ұзындығы инерция радиусының (i_x) шамасына тең (5. 9-сурет). Инерция радиусы арқылы, инерция моментін келесі формуламен анықтауға болады

.

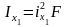16 – сұрақ