Тема 5. Линейные операторы и их матрицы в данном базисе. Собственные векторы и собственные значения. Самосопряженные операторы. Понятие о квадратичных формах в Rn .

Предположим, что в векторном пространстве задан закон, по которому каждому вектору данного пространства ставится в соответствие вектор из этого пространства. Символически мы это будем записывать так .

Или когда не возникает необходимости, скобку будем опускать .

При этом этот закон обладает определенными свойствами, а именно

1.

2. .

Тогда мы будем говорить, что в пространстве задан линейный оператор .

Зададимся вопросом, а когда мы полностью знаем линейный оператор? Ответ очевиден – мы полностью знаем линейный оператор, когда можем сказать, в какой вектор превращается по его действием любой вектор пространства. А теперь зададимся вопросом, какой минимальной информацией надо обладать, чтобы ответить на первый вопрос. Будем рассуждать по следующей схеме. Пусть в векторном пространстве имеется базис . Тогда любой вектор данного пространства можно представить в виде .

Тогда . В силу линейности оператора имеем . То есть, достаточно знать, во что под действием этого оператора превращаются векторы базиса.

Пусть вектор-столбцы соответствующих образов векторов базиса соответственно равны:

.

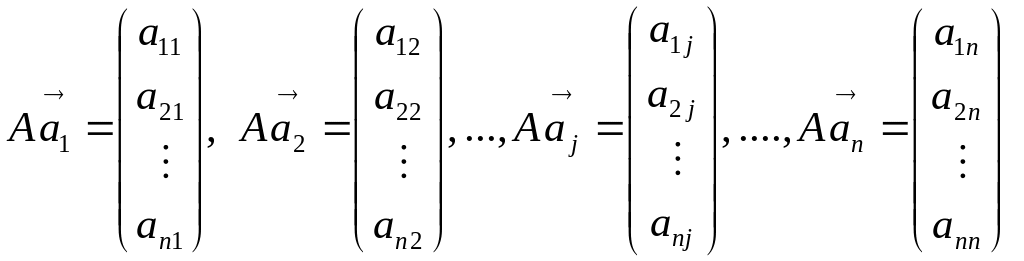Матрицей линейного оператора А назовем матрицу А размерности ( ) вида - столбцы матрицы А – это координаты образов соответствующих базисных векторов.

Пусть , при этом вектор имеет следующий вектор-столбец координат . Вектор-столбец координат вектора представим в виде .

Тогда

.

То есть

.

Теперь если мы вспомним умножение матриц, то выражение, которое мы получили, в матричной форме записывается достаточно просто

.

Или совсем кратко , где А – матрица, , - вектор-столбцы соответствующих координат.

То есть действие любого линейного оператора эквивалентно умножению вектор-столбца координат на некоторую матрицу.

С другой стороны, если действие оператора представить в виде , где А – произвольная матрица, то мы получим линейный оператор просто в силу свойств операции умножения матриц. Таким образом, линейные операторы и квадратные матрицы размерности находятся во взаимнооднозначном соответствии.

Вместе с тем матрица линейного оператора привязана к конкретному базису. Но оператор действует независимо от базиса. Система координат нужна нам с вами, чтобы каким-то образом его записать. Поэтому зададимся вопросом, а как меняется матрица линейного оператора при изменении базиса.

Пусть имеется базис - назовем его старым. В этом базисе матрица линейного оператора равна , и имеется вектор-столбцы , - соответствующих координат векторов, при этом .

Пусть имеется также базис - назовем его новым. В этом базисе матрица того же линейного оператора равна , и вектор-столбцы , - соответствующих координат тех же векторов , при этом .

Пусть - матрица перехода. Тогда имеем , . Значит, , , . Но поскольку , то . Полученная формула и характеризует изменение матрицы линейного оператора при изменении базиса.

Рассмотрим такой вектор , который под действием линейного оператора остается колинеарен самому себе, то есть . Такой вектор называется собственным, а число называется собственным значением линейного оператора. Отметим, что собственный вектор определен с точностью до постоянного множителя. Далее попытаемся отыскать способ определения собственных значений и собственных векторов.

Тождественным оператором назовем такой линейный оператор, что . Заметим, что тождественному оператору соответствует единичная матрица .

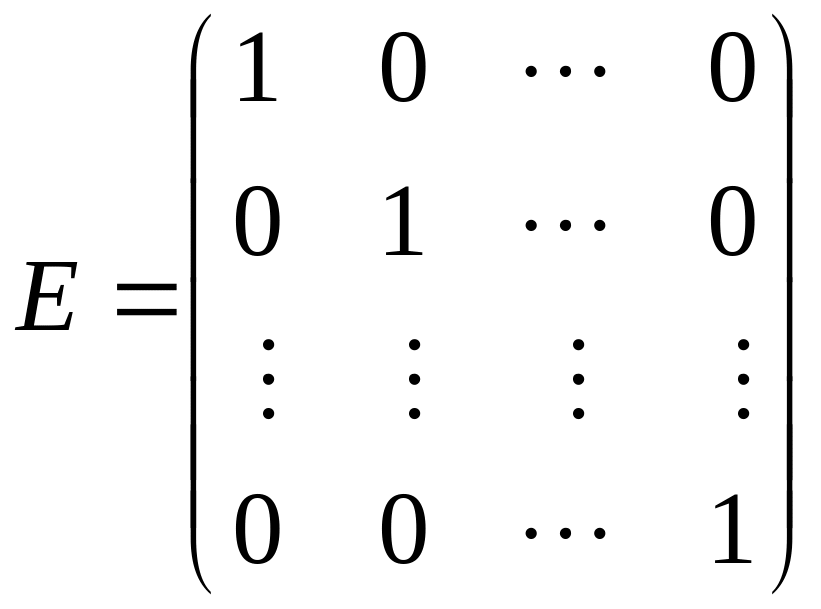В матричном виде уравнение для определения собственных векторов и собственных значений записывается в виде , или, что тоже самое,

,

Последнее уравнение можно рассматривать как линейную систему однородных уравнений с неизвестными. Такая система может иметь ненулевое решение только в том случае, когда ее определитель равен нулю. Тогда уравнение для определения имеет вид .Зная , мы можем определить собственные векторы.

Рассмотрим пример. Найти собственные значения линейного оператора и единичные собственные векторы, составляющие острый угол с осью X

Пусть собственный вектор имеет вид .

Тогда имеем .

Или получаем систему уравнений .

Из условия равенства нулю определителя системы имеем уравнение для определения собственного значения _.

.

Найдем собственные векторы.

Пусть . Имеем, с учетом того, что вектора единичные

, , , .

Поскольку вектор составляет острый угол с осью Х, то первый собственный вектор имеет координаты .

Аналогично . Имеем, с учетом того, что вектора единичные

, , , .

Поскольку вектор составляет острый угол с осью Х, то второй собственный вектор имеет координаты .

Представим наглядно действие этого оператора. Имеются два собственных вектора , и произвольный вектор

На первом этапе вектор раскладывается по двум составляющим,

То есть представляется в виде = +

На втором этапе преобразуются составляющие

, .

Затем эти составляющие складываются.

Следующее понятие, которое мы рассмотрим – это самосопряженные операторы. Мы будем в дальнейшем предполагать, что векторы заданы координатами в ортонормированном базисе. Наряду с вектор-столбцом мы будем рассматривать вектор-строку .

Тогда скалярное произведение векторов ,

Удобно записывать как произведение матриц

Определение. Оператор A называется самосопряженным, если для любых двух векторов , выполнено .

Теорема. Оператор A самосопряженный тогда и только тогда, когда его матрица симметрична относительно главной диагонали.

Доказательство.

Пусть матрица оператора А равна .

Пусть она симметрична относительно главной диагонали ,и ,

Тогда . .

С другой стороны .

Так как , то .

Теперь докажем необходимость.

Пусть , где при , ; , где при , .

, , так как , то .

Квадратичной формой называется выражение вида

= , где А самосопряженный оператор. Заметим, что квадратичную форму можно записать как произведение матриц

=

В частности рассмотрим пример на плоскости.

Пусть матрица оператора имеет вид . Тогда , .

Вам не напоминает это выражение кое-что из кривых второго порядка?

Теперь рассмотрим квадратичную форму на единичной сфере, то есть для таких векторов, у которых норма равна единице. На этой сфере квадратичная форма принимает наибольшее значение. Пусть оно достигается на векторе , где . Рассмотрим произвольный вектор ортогональный , равный по норме единице . Тогда вектор имеет единичную норму. Исследуем функцию . Эта функция достигает максимума при .

Имеем

Так как оператор А самосопряженный, то .

Тогда .

Поскольку данная функция принимает максимум при , то при . Имеем = . Полагая , получаем = . Так как , то . То есть вектор ортогонален любому вектору ортогональному . Значит колинеарен . То есть . Это означает, что вектор является собственным вектором оператора А, а число его собственным значением.

Точно так же поступая с остальными векторами, ортогональными , найдем следующий собственный вектор. И так далее. Получаем принципиальный вывод, что у самосопряженного оператора существует ортонормированный базис из собственных векторов , которым соответствуют собственные значения .

В таком ортонормированном базисе матрица оператора А имеет диагональный вид

.

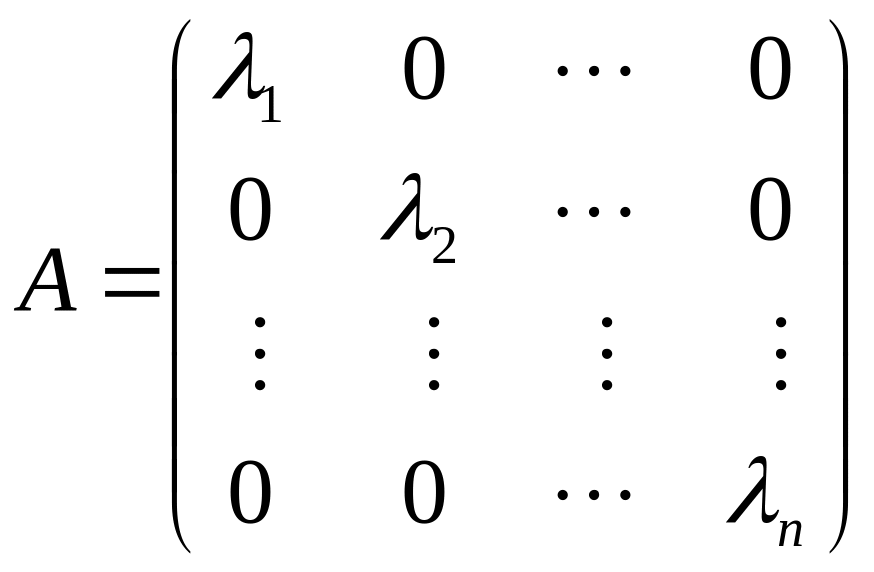Соответствующая квадратичная форма имеет вид .