Моделирование_Лаба_4

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

Ассистент				Иванова М.С
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №4

Моделирование случайной вектора

по курсу: Моделирование

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4616				А.В.Павлов
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2019

Цель работы:

1) ознакомление с графическими возможностями системы MATLAB по изучению основных законов распределений случайных векторов, визуализированное исследование

зависимости графиков функций распределения и функций плотности вероятности от параметров распределений;

2) изучение возможностей системы MATLAB по моделированию случайных векторов.

Вариант №8.

Нормальный закон распределения

close all;

clc;

clear all;

n=2; %размерность случайного вектора

N=500; %количество наблюдений (объем выборки)

U=randn(n,N);% генерация случайного вектора

cov_u = eye(n,n); %ковариационная матрица

cov_ksi=[1 0;0 1]; %ввод ковариационной матрицы

M_ksi=[0;0]; %ввод матрицы

% M_ksi=zeros(n,1);

A=zeros(n,n);

%вычисление элементов матрицы

for i=1:n,

for j=1:i,

sum=0;

for k=1:(j-1),

sum=sum+A(i,k)*A(j,k)*cov_u(k,k);

end

if i==j

A(i,j)=sqrt((cov_ksi(i,j)-sum)/cov_u(j,j));

else

A(i,j)=(cov_ksi(i,j)-sum)/(A(j,j)*cov_u(j,j));

end

end

end

%построение случайного вектора

for i=1:N,

ksi(:,i)=A*U(:,i)+M_ksi;

end

%транспонирование матрицы случайных векторов

ksi_t=ksi';

disp('Матрица преобразований A');

A

disp('Выборка входных векторов U');

U

disp('Выходные векторы ksi');

ksi

disp('Исходн. матрица cov_ksi');

cov_ksi

%построение выборочной ковариационной матрицы

disp('Выборочн. ков. матрица cov_ksi');

test_cov_ksi=cov(ksi_t)

%проверка правильности преобразований

disp('Матрица cov_ksi (проверка правильности преобразований)');

A*cov_u*A'

%построение гистограмм для входных и выходных векторов

figure();

hist(U',20);

xlabel('Интервалы');

ylabel('Количество попаданий');

title('Гистограмма для каждой из компоненты входного двумерного случайного вектора (x1,x2)','FontSize',14);

legend('x1','x2')

figure();

hist(ksi',50);

xlabel('Интервалы');

ylabel('Количество попаданий');

title('Гистограмма для каждой из компоненты выходного двумерного случайного вектора (x1,x2)','FontSize',14);

legend('x1','x2')

figure();

subplot(2,1,1),plot(U');

xlabel('номер эксперимента,n');

ylabel('Пара значений (x1,x2) n-го экспе-та');

title('Входной двумерный случайный вектор (x1,x2)','FontSize',14);

subplot(2,1,2),plot(ksi_t);

xlabel('Номер эксперимента,n');

ylabel('Пара значений (x1,x2) n-го экспе-та');

title('Выходной двумерный случайный вектор (x1,x2)','FontSize',14);

mean(ksi_t)

mean(U')

var(ksi_t)

var(U')

M=300;

z=zeros(M);

test_z=zeros(M);

for i=1:M

x(i)=i/37.5-4;

for j=1:M

y(j)= j/37.5-4;

WW= 1 / ( 2*pi*cov_ksi(1,1)*cov_ksi(2,2)*sqrt( 1-cov_ksi(1,2)^2 )) ;

WW1=-1/(2*(1-cov_ksi(1,2)^2));

WW2= ((x(i)- M_ksi(1))^2)/(cov_ksi(1,1)^2);

WW3=(2*cov_ksi(1,2)*(x(i)-M_ksi(1))*(y(j)-M_ksi(2)))/(cov_ksi(1,1)*cov_ksi(2,2));

WW4= ((y(j)- M_ksi(2))^2)/(cov_ksi(2,2)^2);

z(i,j)= exp((WW2+WW4-WW3)*WW1)*WW;

WW= 1 / ( 2*pi*test_cov_ksi(1,1)*test_cov_ksi(2,2)*sqrt( 1-test_cov_ksi(1,2)^2 ) ) ;

WW1=-1/(2*(1-test_cov_ksi(1,2)^2));

WW2= ((x(i)- M_ksi(1))^2)/(test_cov_ksi(1,1)^2);

WW3=(2*test_cov_ksi(1,2)*(x(i)-M_ksi(1))*(y(j)-M_ksi(2)))/(test_cov_ksi(1,1)*test_cov_ksi(2,2));

WW4= ((y(j)- M_ksi(2))^2)/(test_cov_ksi(2,2)^2);

test_z(i,j)= exp((WW2+WW4-WW3)*WW1)*WW;

end

end

figure();

mesh(x,y,z);

xlabel('x1');

ylabel('y2');

zlabel(' p(x1,x2)')

title('Плотность (теоретическая) вероятности p(x1,x2)двумерного случайного вектора (x1,x2)','FontSize',14);

figure();

mesh(x,y,test_z);

grid on;

xlabel('x1');

ylabel('x2');

zlabel('p(x1,x2)')

title('Плотность (экспериментальная) вероятности p(x1,x2)двумерного случайного вектора (x1,x2)','FontSize',14);

figure();

[C,h]=contourf(x,y,z);

clabel(C,h);

grid on;

xlabel('x1');

ylabel('x2');

title('Контурный график (теоретический) плотности вероятности p(x1,x2) двумерного случайного вектора (x1,x2)','FontSize',14);

axis('equal')

figure();

[C,h]=contourf(x,y,test_z);

clabel(C,h);

grid on;

xlabel('x1');

ylabel('x2');

title('Контурный график (экспериментальный) плотности вероятности p(x1,x2) двумерного случайного вектора (x1,x2)','FontSize',14);

axis('equal')

Полученные графики:

Рисунок 1 – Гистограмма для каждой компоненты входного двумерного случ. вектора

Рисунок 2 – Гистограмма для каждой из компоненты выходного двумерного случ. Вектора

Рисунок 3 – Входные и выходные случ. Вектора

Рисунок 4 – Плотность вероятности двумерного случайного вектора

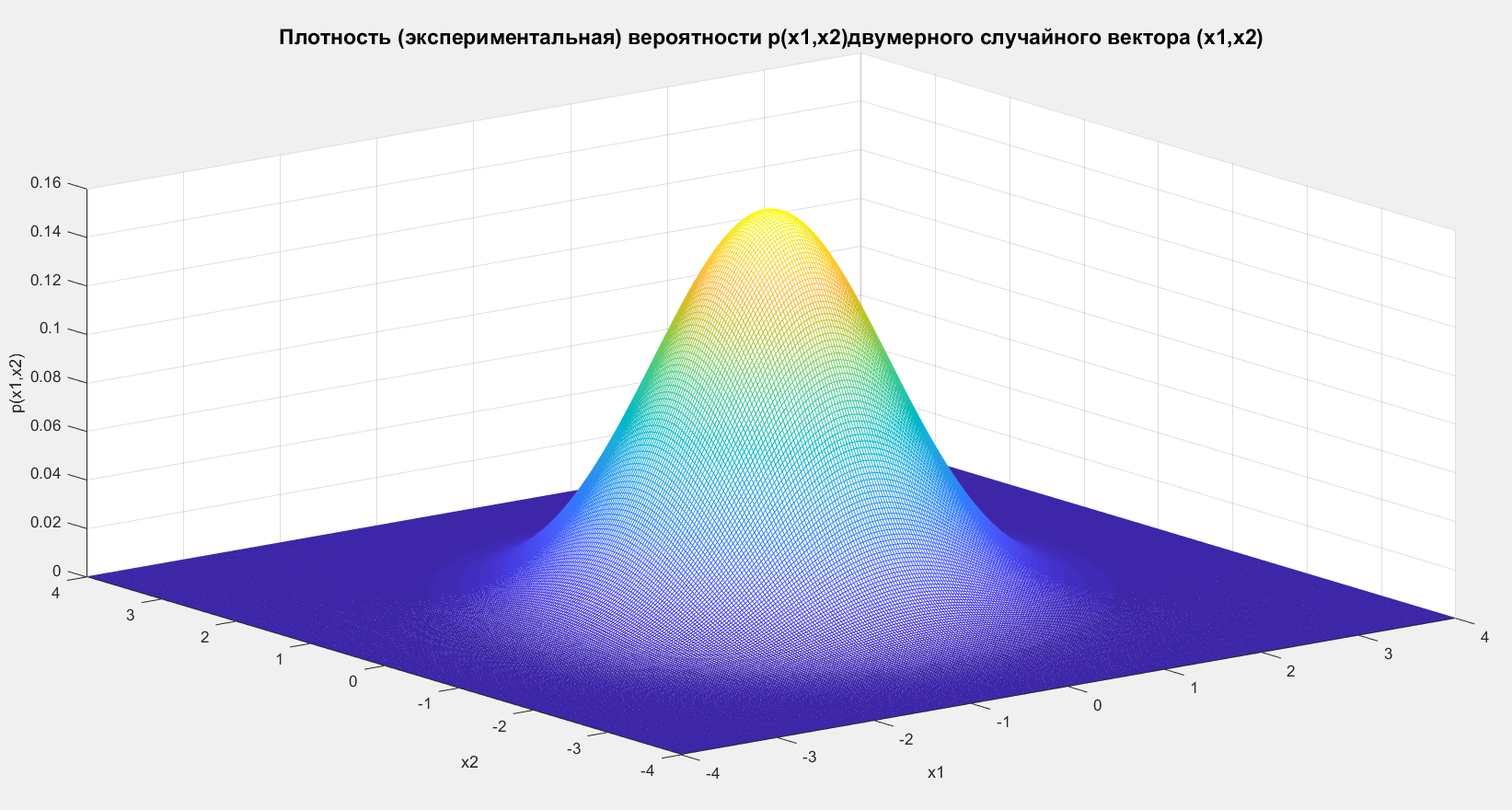
Рисунок 5 – Плотность экспериментальная вероятности двумерного случайного вектора

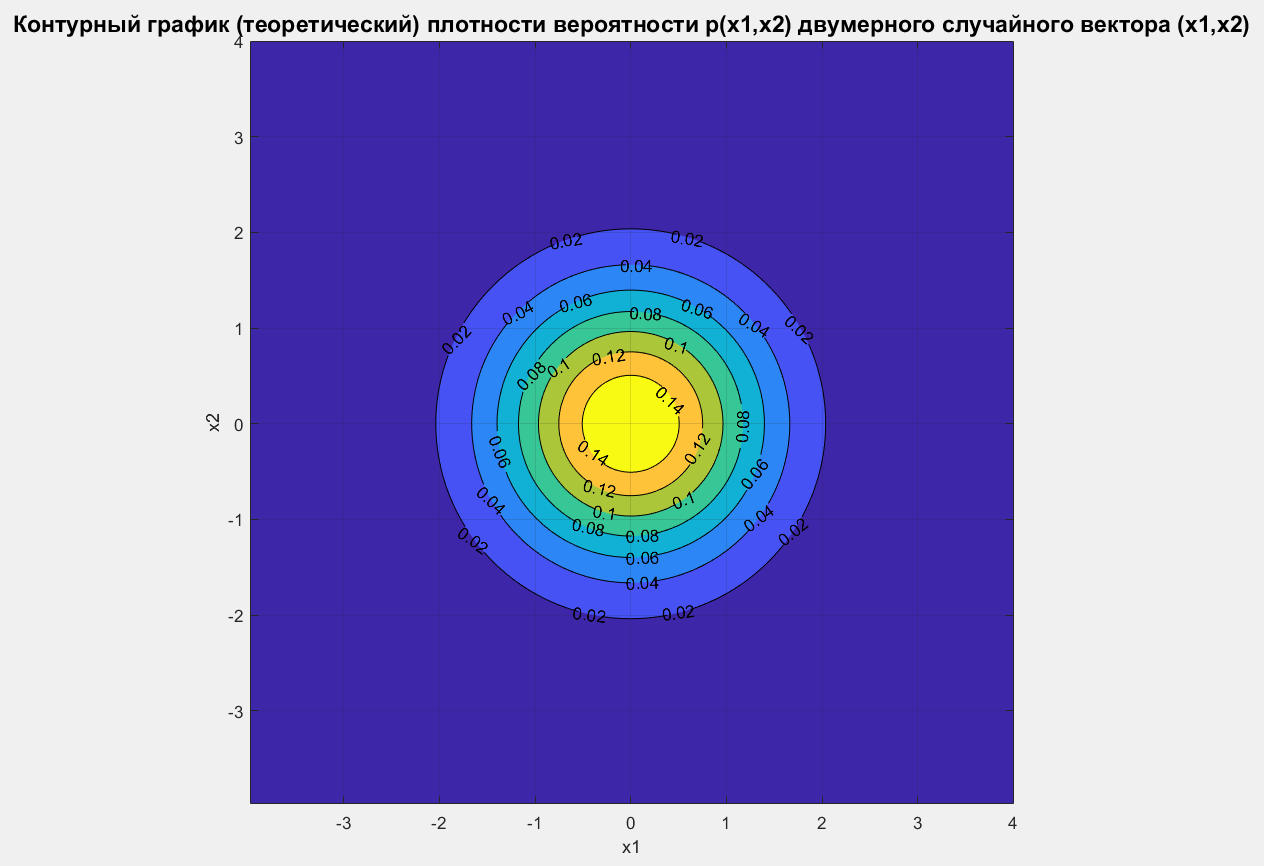
Рисунок 6 – Контурный график

Вывод: В ходе лабораторной работе мы промоделировали случайный вектор, ознакомились с графическими возможностями системы MATLAB по изучению основных законов распределений случайных векторов. Изучили возможности системы MATLAB по моделированию случайных векторов

9