Моделирование_Лаба_1

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

ассистент				Иванова М.С
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1

Исследование датчиков равномерно распределенных псевдослучайных чисел.

по курсу: Моделирование

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4616				А.В.Павлов
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2019

Цель работы: ознакомление с методами и алгоритмами моделирования

в программной среде MathCAD или MatLab случайных событий, а также

изучение тестов для проверки качества моделирования.

Вариант №1. Мультипликативные датчики

Листинг

import numpy as np

import scipy.stats as st

import matplotlib.pyplot as plt

R=0.0003

k=100

p=3

M=5**(2*p+1)

print(M)

R_data=[]

d1=[]

d2=[]

B=[]

d3=[]

R_random= np.random.uniform(0,1,k)

d4=st.uniform.pdf(R_random,loc=0, scale=1)

for i in range(k):

R=M*R

R=R % int(R)

R_data.append(R)

d1.append(abs(R-(i-1)/k))

d2.append(abs(R-i/k))

for i in range(k):

d3.append((R_data[i]-d4[i]))

d1=max(d1)

d2=max(d2)

print(d1)

print(d2)

print(max(d3))

cdf = st.binom.cdf

#2 плотности распред(гистгорма), 2 импр функ расперд, 2 корр= 15 графиков

#Для 100 считаем на глаз, для 600 и 1000 трассировкой

col=np.correlate(R_data, R_data[::-1],'full')

col2=np.correlate(R_random, R_random[::-1],'full')

#print(len(col))

X= np.linspace(0,1,len(R_data))

plt.plot(np.linspace(0,len(col),len(col)),col,alpha=0.3,color='black')

plt.plot(np.linspace(0,len(col2),len(col2)),col2)

plt.show()

#plt.hist(st.uniform.cdf(R_data,0,1),9)

plt.plot(np.sort(R_random),st.uniform.cdf(np.sort(R_random),loc=0, scale=1),'k-')

#plt.plot(np.sort(R_random),st.uniform.cdf(R_random,loc=0, scale=1))

#plt.hist(np.sort(R_data),density=False,cumulative=True,histtype='step')

#plt.hist(np.sort(R_random),density=False,cumulative=True)

#plt.show()

sorted_data = np.sort(R_data)

yvals=np.arange(len(sorted_data))/float(len(sorted_data)-1)

plt.plot(sorted_data,yvals)

plt.show()

sorted_data = np.sort(R_random)

yvals=np.arange(len(sorted_data))/float(len(sorted_data)-1)

plt.plot(sorted_data,yvals)

plt.show()

d=st.kstest(R_data,'norm')

print(d)

P=1-2*np.exp(-2*k*(0.010693447358789854)**2)

print("Ответ")

print(P)

Результат работы программы при k=100.

Вероятность P~0.7523

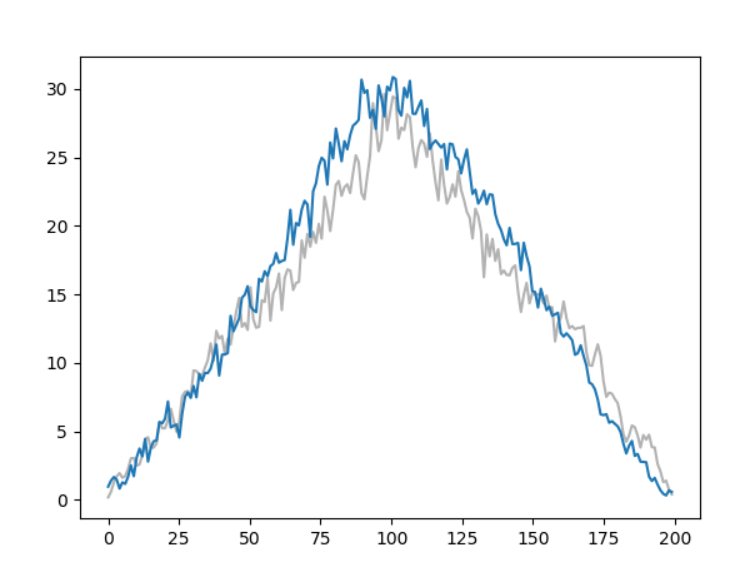
Рисунок 1 – Корреляция при k=100

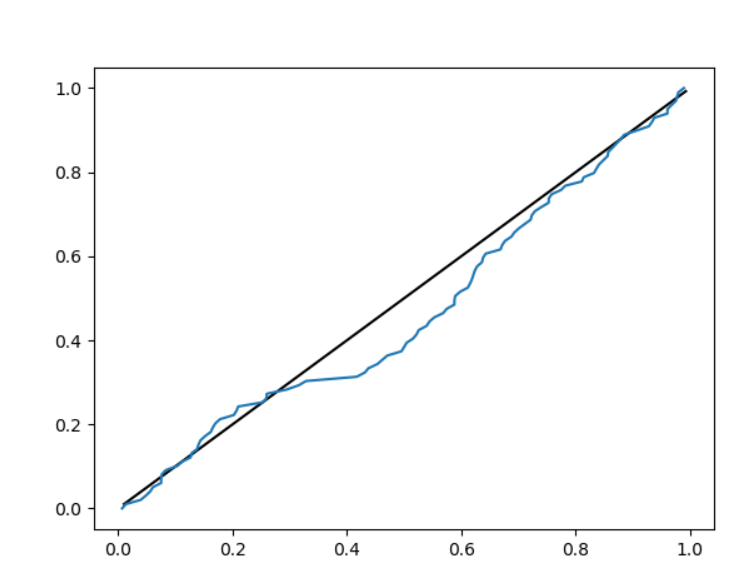
Рисунок 2 – эмпирическая функция k=100

Рисунок 3 – эмпирическая функция k=100 для случайных данных

Рисунок 4 – Плотность распределения k=100

Рисунок 5 – Плотность распределения случайных велечин k=100

Результат работы при k=600.

Вероятность P~0.8634

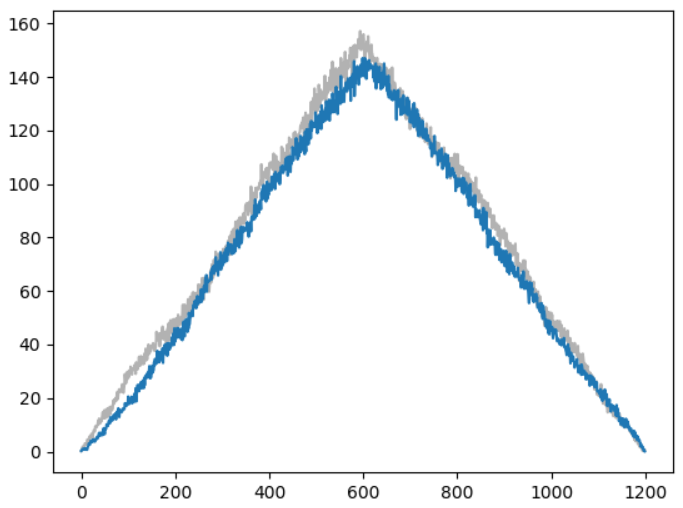
Рисунок 6 – Корреляция при k=600

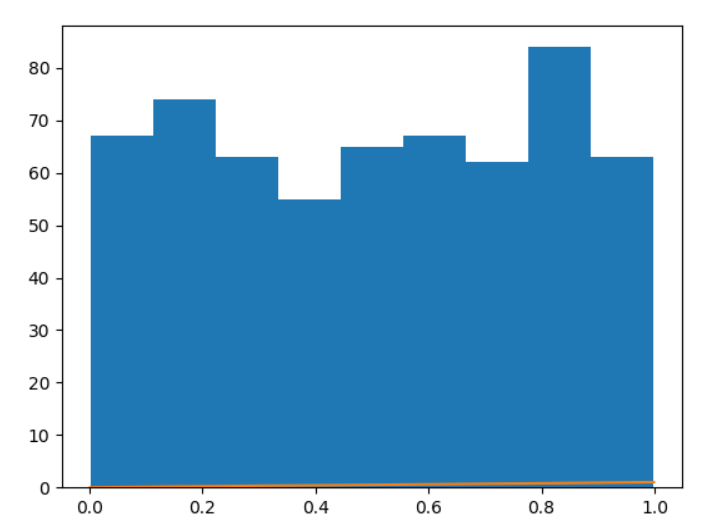
Рисунок 7 – Плотность распределения случайных величин k=600

Рисунок 8 – Плотность распределения k=600

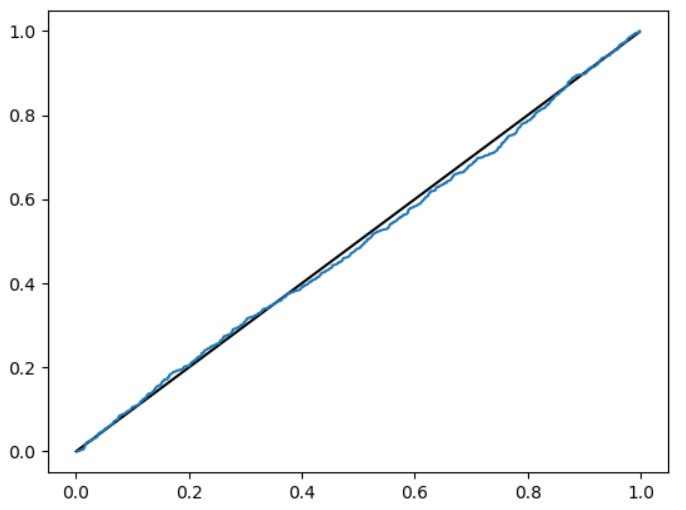
Рисунок 9 – эмпирическая функция k=600

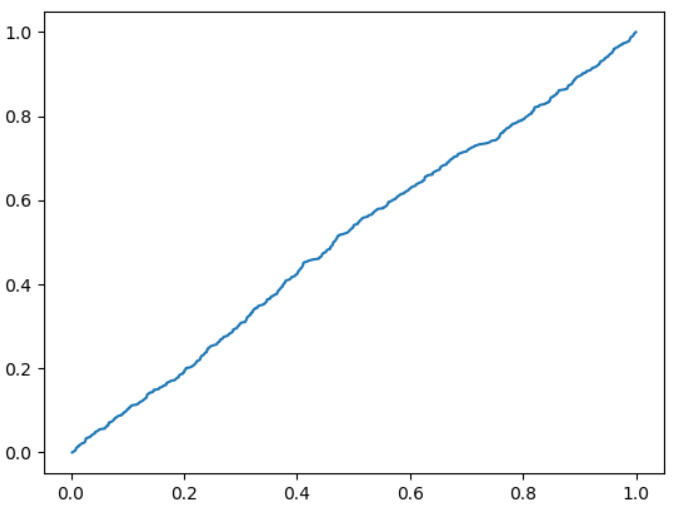
Рисунок 10 – эмпирическая функция случайного распределения k=600

Результат работы при k=1000

Вероятность P~0.9843

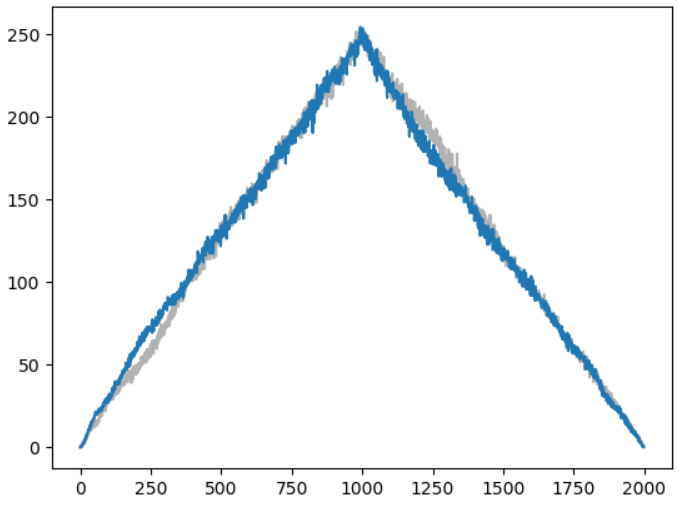
Рисунок 11 – Корреляция при k=1000

Рисунок 12 – эмпирическая функция k=1000

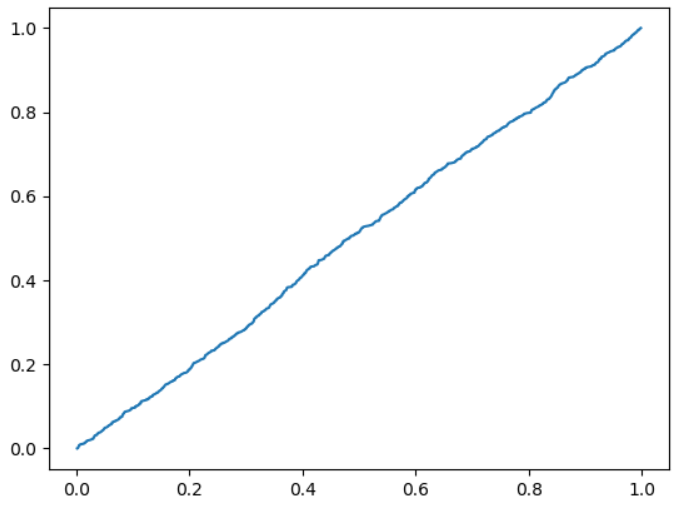
Рисунок 13 – эмпирическая функция случайного распределения k=1000

Рисунок 14 – Плотность распределения k=1000

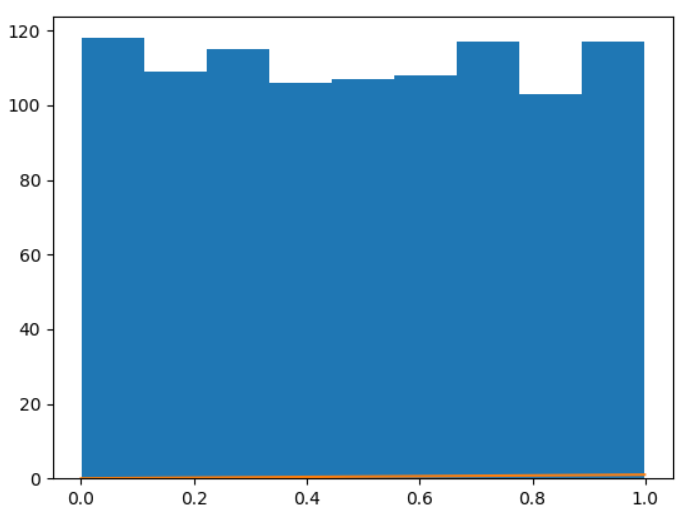
Рисунок 15 – Плотность распределения k=1000

Вывод: В ходе лабораторной работе я написал программу, где используется мультипликативные датчики, а также встроенную библиотеку для генерации случайных чисел.

В результате работы программы видно, что с возрастанием количества чисел увеличивается вероятность того что выборка является равномерной. А разница между теоретической и реальной эмпирической функции уменьшается.

Список использованных источников

1. Преснякова Г.В., Шахомиров А.В. Проектирование реляционных баз данных: учебное пособие. СПб.: ГУАП, 2015. 125с.

2. Карчевский Е.М., Филиппов И.Е., Филиппова И.А. Access 2010 в примерах: учебное пособие. Казань: Казанский университет, 2012. 140с.