15. Сопротивления в цепи синусоидального тока.

Введем теперь ряд величин, характеризующих цепь синусоидального тока.

Отношение комплексного напряжения к комплексному току называется комплексным сопротивлением где —отношение действующего или амплитудного напряжения соответственно к действующему или амплитудному току называется полным сопротивлением. Полное сопротивление равно модулю комплексного сопротивления. Аргумент комплексного сопротивления равен разности фаз напряжения и тока, т. е.

Комплексное сопротивление можно представить в виде

где — вещественная часть комплексного сопротивления, называется активным сопротивлением; — значение мнимой части комплексного сопротивления, называется реактивным сопротивлением.

Очевидно, что

Из выражения следует, что для схемы, , комплексное сопротивление причем реактивное сопротивление

где

называются соответственно индуктивным и емкостным сопротивлениями. Из выражения видно, что индуктивное сопротивление связывает между собой амплитуды напряжения на индуктивности и тока:

Индуктивное сопротивление прямо пропорционально частоте тока. Это объясняется тем, что напряжение на индуктивности пропорционально скорости изменения тока: Емкостное сопротивление, как следует из выражения ,связывает между собой амплитуды напряжения на емкости и тока:

Емкостное сопротивление обратно пропорционально частоте тока. Эту зависимость от частоты легко пояснить, если считать заданным напряжение на зажимах емкости, а искомой величиной ток: . Ток прямо пропорционален скорости изменения напряжения на зажимах емкости и, следовательно, емкостное сопротивление обратно пропорционально частоте напряжения.

Напряжения на последовательно соединенных индуктивности и емкости противоположны по фазе; поэтому в выражение для реактивного сопротивления сопротивления и входят с различными знаками. Напряжения на индуктивности и на емкости сдвинуты по фазе относительно напряжения на сопротивлении соответственно на и Поэтому эти сопротивления входят в Z как г, и .

Следует обратить внимание на то, что индуктивное и емкостное сопротивления являются величинами арифметическими — положительными, а реактивное сопротивление — величина алгебраическая и может быть как больше, так и меньше нуля.

Для ветви, содержащей только индуктивность, реактивное сопротивление равно индуктивному сопротивлению , а реактивное сопротивление ветви, содержащей только емкость, равно емкостному сопротивлению, взятому со знаком минус, т. е. — . Для ветвей, каждая из которых содержит только сопротивление г, только индуктивность L или только емкость , комплексные сопротивления соответственно равны:

16. Индуктивный элемент в цепи синусоидального тока.

Рассмотрим электрическую цепь, куда включен индуктивный элемент. И пусть в цепи действует мгновенный ток.

i=

П ри прохождении по индуктивности переменного тока в нем возбуждается ЭДС самоиндукции , L-индуктивность катушки, 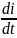- скорость изменения тока

Учитывая, что в цепи действует некое напряжение по закону Ома для постоянного тока применяемого для мгновенных значений получим: ;

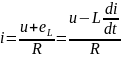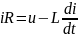
если катушка индуктивности идеальная, то сопротивление R=0.

Тогда сопротивление в цепи равно:

; +

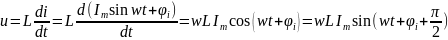
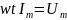
При синусоидальном токе напряжение на индуктивном элементе изменяется с той же частотой , что и ток, но опережает ток на четверть периода (т.е. /2).Следовательно сдвиг фаз

Величина 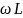, имеющая размерность Ом называют индуктивным сопротивлением и обозначают X_L =

Um=X_LI_m - закон Ома для амплитудных значений

В комплексной форме сопротивление индуктивности определяется следующим образом

;

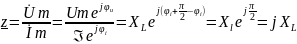
К омплексное сопротивление индуктивного элемента является минимальным положительным числом модуль которого равен X_L , векторная диаграмма для индуктивного элемента имеет следующий вид

Мгновенная мощность индуктивного элемента характеризует работу ,выполняемую за период

Первая четверть периода мгновенная мощность положительна, это означает, что индуктивный элемент потребляет энергию от источника , во второй четверти периода мгновенная мощность отрицательна, это означает, что индуктивный элемент отдает запасенную магнитным полем энергию во внешнюю цепь, при этом энергия запасенная и энергия высвобожденная равны между собой, т.к. кривые ограничены синусоидой мощности, таким образом в цепи с индуктивным элементом не совершается работа, а происходит периодический обмен энергии между источником и магнитным полем

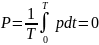-активная мощность за период равна 0

Интенсивность этого обмена характеризуется наибольшей скоростью поступления энергии в магнитное поле и эта величина называется реактивной мощностью (Q_L) Q_L =IU=I²X_L [ВАР]