5. Эквивалентные преобразования пассивных участков электрических цепей.

Существует 4 основных вида соединения элементов:

1) последовательное; 2) параллельное; 3) соединение звездой;

4) соединение треугольником.

1. I_об = I₁ = I₂ = I_n U_об = U₁ + U₂ + U_n R_об = R₁ + R₂ + R_n

2. I_об = I₁ + I₂ + I_n U_об = U₁ = U₂ = U_n 1/R = 1/R₁ + 1/R₂ + 1/R_n

3. В сложной ЭЦ встречаются соединения, которые нельзя отнести ни к последовательному, ни к параллельному.

Рассмотрим мостовую цепь (используется в измерительных устройствах).

В такой схеме часть цепи образует треугольник, вершинами которого являются 3 узла A, B, C, а сторонами являются сопротивления R_ab, R_bc, R_ca.

Расчет такой цепи удобно производить, используя эквивалентную замену 3-х ветвей, соедин. треугольником, 3-мя ветвями, соедин. звездой. Определим соотношение эквивалентности между сопротивлениями обеих схем.

Общее условие эквивалентности: напряжение и токи в ветвях не подвергнуты преобразованию, должны оставаться без изменения в любых режимах, в т.ч. при размыкании ветвей, присоединенных к узлам A, B, C.

При отсоединении резисторов R_ad от т. A в обеих схемах ток узла A и С, а также напряжение U_bc должны быть равны. А если это так, то и сопротивление R_bc на 1-й схеме должно быть равно сопротивлению между узлами В и С 2-й схемы.

I_C1 = I_C2 I_B1 = I_B2 U_BC1 = U_BC2 R_BC1 = R_BC2

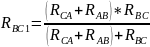
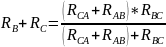
Аналогично, отсоединяя резистор R_CD от т. C, получим след. выражение:

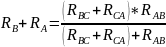
Решая систему полученных уравнений относительно R_A+R_B+R_C, получим след. отношение:

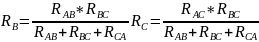
Если резисторы различного сопротивления (для обратного перехода из звезды в треугольник):

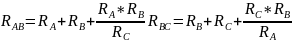
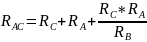
Схема 1 (треугольник): Схема 2 (звезда):

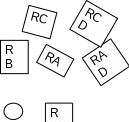
C С

B D B D

A

E A

6. Метод контурных токов.

Если цепь содержит много узлов и контуров, то расчет ЭЦ на основе применения з-в Кирхгофа связан с решением большого кол-ва уравнений.

Число уравнений, составленных по методу контурных токов, равно количеству уравнений, составляемых по второму закону Кирхгофа. Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах.

Введя понятие о контурных токах можно уменьшить кол-во уравнений на величину, равную составляемым по 1-му з-ну К-фа (у-1; где у – кол-во узлов).

Порядок расчета: Выбираются независимые контуры, и задаются произвольные направления контурных токов.

Контурные токи – условные (расчетные) токи, замыкающиеся в соответствующих контурах.

Задача: найти все токи.

После выбора положит. направления токов на схеме выбираются независим. контуры и положит. направления обхода каждого контура.

Считается, что в каждом контуре циркулирует свой собственный контурный ток, направление которого совпадает с выбранным направлением в контуре.

I₁ = I_I; I₂ = I_II - I_I; I₃ = I_II; I₄ = I_II –I_III; I₅ = - I_III

Для определения контурн. токов по 2-му закону К-фа составляются уравнения для выбранных контуров:

1) I_I (R₁+R₂) – I_II *R₂ = E₁ – E₂

2) I_II (R₂+R₃ +R₄) – I_I *R₂ - I_III *R₄ = E₂

3) I_III (R₄+R₅) - I_II *R₄ = - E₃

Все резисторы, входящие в 1-й контур – R₁₁, во 2-й - R₂₂, в 3-й – R₃₃.

R ₁₁ = R₁ + R₂

R₂₂ = R₂ + R₃ + R₄

R₃₃ = R₄ + R₅

Резисторы, общие с 1-м и 2-м контуром - R₁₂ или R₂₁, со 2-м и 3-м – R₂₃ или R₃₂, 1-м и 3-м - R₁₃ или R₃₁.

R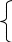 ₁₂ = R₂₁ = R₂

R₁₃ = R₃₁ = 0

R₂₃ = R₃₂ = R₄

Источники тока или напряжения, входящие в 1-й контур –

Е₁₁ = Е₁ - Е₂; 2-й: Е₂₂ = Е₂; 3-й: Е₃₃ = - Е₃

Система уравнений будет представлена в след. виде:

R₁₁ * I_I - R₁₂ * I_II - R₁₃ * I_III = E₁₁

- R₂₁ * I_I + R₂₂ * I_II – R₂₃ * I_III = E₂₂

- R₃₁ * I_I – R₃₂ * I_II + R₃₃ * I_III = E₃₃

На главной диагонали все положительные, остальные – отрицательные.

Матричная форма записи системы удобна для решения системы при помощи ЭВМ.

При расчете электрических цепей изложенным методом всегда стремятся к тому, чтобы число контурных токов, замыкающихся через каждую из ветвей, было по возможности минимальным. С этой целью обычно выбирают каждый контур в виде ячейки руководствуясь указанным выше правилом выбора независимых контуров при составлении уравнений на основании второго закона Кирхгофа, что возможно для любой планарной схемы. Положительные направления контурных токов можно выбирать и произвольно, т. е. независимо от положительных направлений токов в ветвях.