4. Билет 4

ЭКВИВАЛЕНТНОСТЬ МНОЖЕСТВ. НЕСЧЁТНОСТЬ МНОЖЕСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ. ПОНЯТИЕ МОЩНОСТИ

Рассмотрим вопрос об эквивалентности множеств.

Два произвольных множества М₁ и М₂ эквивалентны, если между их элементами можно установить взаимно однозначное соответствие.

Обозначение : М₁ ≈ М₂

Два конечных множества эквивалентны тогда, когда имеют одинаковое количество элементов.

Если два множества эквивалентны третьему, то они эквивалентны между собой.

Все счётные множества эквивалентны.

Примеры.

1. Любые два отрезка эквивалентны.

[a,b]≈[c,d]

2. К 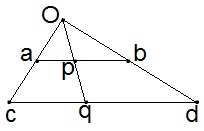омплексная плоскость (С) и поверхность некоторой сферы эквивалентны.

3. О 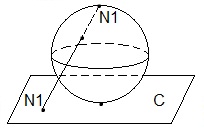трезок без концевых точек эквивалентен числовой прямой

(аналитически) : y=(1/π)arctg(x)+1/2

В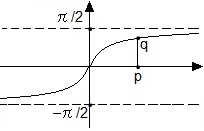 рассмотренных примерах легко заметить, что бесконечное множество было эквивалентно некоторой своей части. (натуральных чисел столько же, сколько рациональных). Но это справедливо и для других бесконечных множеств.

Утверждение.

Каждое бесконечное множество эквивалентно своей истинной части.

Доказательство:

Пусть М — некоторое бесконечное множество. Выделим из него счётное множество А. Его можно разделить на два счётных множества: А1={а₁, а_3, а₅ …}, А2={а₂, а₄, а₆ …}

А эквивалентно А₁

Это взаимно однозначное соответствие можно продолжить на такие множества:

AU(M\A)=M ≈ M\A₂=A₁U(M\A)

M\A₂ – истинная часть множества М.

Следовательно, каждое бесконечное множество эквивалентно своей истинной части.

Теорема.

Множество точек, заключённых между 0 и 1 на числовой прямой, - это несчётное множество. (оно бесконечно и не эквивалентно счётным множествам)

Доказательство:

Представим числа, заключённые между 0 и 1 в виде перечня бесконечных десятичных дробей (в него могут попасть все или некоторое из этих чисел).

α₁=0,а₁₁,а₁₂,а₁₃…а_1n…

α₂=0,a₂₁,a₂₂,a₂₃...a_2n...

α₃=0,a₃₁,a₃₂,a₃₃...a_3n...

…

α_n=0,a_n1,a_n2,a_n3...a_nn...

…

a(ij) — десятичные цифры, стоящие на соответствующем месте.

Построим бесконечную десятичную дробь β по следующему правилу:

β=0, β₁β₂... β_n...

где β₁<>a₁₁, β₂<>a₂₂, … β_n<>a_nn …

Т.е получается, что какой бы перечень под номером 1 мы не взяли, он не может исчерпать всех чисел между 0 и 1. Следовательно, множество таких чисел не счётно.

Но при этом мы должны понимать, что существуют десятичные числа вида: p/10^q. Их счётное множество, и они представимы в виде бесконечных десятичных дробей двумя способами:

5/10 = 0,5000... = 0,4999...

Т.е одно и то же число представимо двумя способами. Чтобы это учесть при построении дроби β, мы должны исключить нули и девятки.

Примеры, связанные с теоремой:

1. [0,1] ≈ [a,b] сегменты

x принадлежит [0,1] х ↔ y = (b-a)x+a, y принадлежит [a,b]

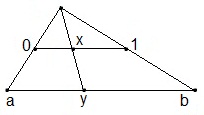
2. (0,1) ≈ R

3. [0,1] ≈ множеству всех точек на плоскости в трёхмерном пространстве

(как следствие : [0,1] ≈ множеству всех прямых на плоскости в трёхмерном пространстве)

Мощностью конечного множества называется количество элементов в нём.

Говорят, что два множества М₁ и М₂ имеют одинаковую мощность, если между элементами этих множеств можно установить взаимно однозначное соответствие. Т.е мощность — это то общее, что есть у всех эквивалентных множеств.

Множество точек, расположенных на числовой оси между 0 и 1 называют множеством мощности континуума. Обозначение : m([0,1])=c.

Следствия из теоремы:

1)множество [0,1] не эквивалентно счётному множеству

2)существование иррациональных чисел. И множество таких чисел является бесконечным несчётным множеством.

Для обозначения эквивалентности множеств А и В используют запись : m(a)=m(B)

Величину m(A), которая является общей характеристикой всех множеств, эквивалентных множеству А, называют кардинальным числом.

Если множество А эквивалентно некоторой части множества В, и в множестве А нет части, эквивалентной множеству В, то считают, что мощность множества А меньше мощности множества В.

Но возможны ещё два случая:

1. Когда множество А содержит подмножество, эквивалентное множеству В, а множество В содержит подмножество, эквивалентное множеству А.

2. Когда А не эквивалентно В, и ни в каком из этих множеств не содержится части, эквивалентной другому множеству.

Тогда в 1) случае А ≈ В (по теореме Кантора-Бернштейна)

Из случая 2) следует, что существуют множества с несравнимыми мощностями. Но оказывается, что такого быть не может. Более того, существуют бесконечные множества, мощность которых больше мощности континуума. И вообще шкала мощностей не ограничена сверху.