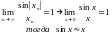72. Билет 29

ЧАСТИЧНЫЕ ПРЕДЕЛЫ ФУНКЦИИ

Может оказаться, что не существует lim f(x) при x → a. Но для некоторых последовательностей {xn}, xn → a, при любом n : xn <> a, всё же существуют пределы lim f(xn) при n → ∞. Такие пределы называются частичными пределами функции f(x) в точке а.

Теорема

Среди всех частичных пределов функции f(x) в точке {a} существует наибольший и наибольшие частичные пределы. Обозначение : lim f(x) и lim f(x) при х → а

Равенство таких пределов имеет место тогда и только тогда, когда существует lim f(x) = g из R при х → а.

Доказательство:

77. Билет 30

БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ

LIM ( SIN X ) / X

Определение

1. Функция f(x) — бесконечно малая при х → a, если lim f(x) = 0

2. Функция f(x) — бесконечно большая при х → a, если lim f(x) = +∞

Классификация бесконечно малых функций:

пусть функции f(x) и g(x) бесконечно малые при х → а.

1. lim f(x)/g(x) = t , t<>0, t из R

функции f(x) и g(x) одного порядка малости при х → a.

Обозначение : f = O(g) или g = O(f)

2. lim f(x)/g(x) = 0

функция f(x) — бесконечно малая высшего порядка, по сравнению с g(x)

Обозначение : f = o(g)

3. lim f(x)/g(x) = Ø

функции f(x) и g(x) несравнимые

4. lim f(x) / (g(x))^k = 0, k из R

f(x) = o(g^k(x))

5. lim f(x) / (g(x))^k = t, t,k из R

f(x) = O(g^k(x))

6. f(x) – g(x) = o(f(x)) ; f(x) – g(x) = o(g(x))

f(x) и g(x) эквивалентные

Обозначение : f(x) ≈ g(x)

Теорема

f(x) ≈ g(x) при х → а. Тогда : lim f(x)/g(x) = 1.

Доказательство:

Пусть f(x) ≈ g(x), тогда f(x) – g(x) = o(g(x))

Рассмотрим следующее :

Обратно:

Пусть lim f(x)/g(x) = 1 при x → a

Тогда δ = ( f(x)/g(x) – 1 ) → 0

γ = f(x) – g(x)

Рассмотрим γ/g(x) = δ → 0 при x → a

То есть γ — более высокого порядка малости, чем g(x)

То есть f(x) – g(x) = o(g(x)) Следовательно, f(x) ≈ g(x)

Теорема

Если f(x) ≈ f₁(x) и g(x) ≈ g₁(x) при х → а. Тогда lim f(x)/g(x) = lim f1(x)/g1(x) = 1

Доказательство:

Классификация бесконечно больших функций:

пусть функции f(x) и g(x) бесконечно большие при х → а.

2. lim f(x)/g(x) = t , t<>0, t из R

функции f(x) и g(x) одного порядка при х → a.

Обозначение : f = O(g) или g = O(f)

2. lim f(x)/g(x) = 0

функция f(x) — бесконечно большая высшего порядка, по сравнению с g(x)

Обозначение : f = o(g)

3. lim f(x)/g(x) = Ø

функции f(x) и g(x) несравнимые

4. lim f(x) / (g(x))^k = 0, k из R

f(x) = o(g^k(x))

5. lim f(x) / (g(x))^k = t, t,k из R

f(x) = O(g^k(x))

6. f(x) – g(x) = o(f(x)) ; f(x) – g(x) = o(g(x))

f(x) и g(x) эквивалентные

Обозначение : f(x) ≈ g(x)

Задача :

Пусть есть произвольная {x_n}, x_n → 0, n → ∞. lim sin(x_n)/(x_n) = ?

Решение :

если 0 < x < π/2, то справедливо : sin(x) < x < tg(x)

S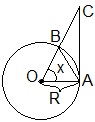 _OAB < S_{сектор OAB} < S_OAC

½ R²sin(x) < ½ R²x < ½ R²tg(x)

sin(x) < x < tg(x)

Пусть x_n → 0, n → ∞. Найдётся k из N такой, что при любом n > k : 0 < |x_n| < π/2

Фиксируем это k.

По неравенству получаем : sin |x_n| < |x_n| < tg |x_n| при n > k

Это неравенство можно разделить на sin |x_n|.

Получаем :

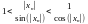
Из этого следует :

Если покажем, что lim cos |x_n| = 1, то найдём требуемый предел.

Рассмотрим : 1 — cos |x_n| = 2 sin2 (|x_n|/2)

Тогда верно следующее:

Воспользуемся принципом сжатой переменной и получим :