2. Достаточность

Пусть lim a_n = lim a_n = +∞

lim a_n = lim v_n = +∞ Следовательно, для любого M из R существует Nm такое, что для любого n > Nm выполнено v_n > M.

Тогда из условия, что a_n >= v_n следует, что при любых n > Nm : a_n > M.

Следовательно, lim a_n = +∞

Теорема о пределе корня.

Пусть lim a_n = a, где a > 0.

q – некоторое число из Z. Тогда :

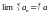
Доказательство:

a_n – возрастающая ограниченная последовательность (действительно : снизу она ограничена 0, если мы работаем в области вещественных чисел, и lim a_n = a). Если же мы работаем в области комплексных чисел, то, начиная с некоторого номера n₀, для любых n > n₀, a_n > 0.

Последовательность 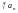тоже возрастает. (т. к a_n – возрастает) И она тоже ограниченна.

А следовательно имеет предел :

36. Билет 19

БЕСКОНЕЧНО МАЛЫЕ ВЕЛИЧИНЫ, ДЕЙСТВИЯ НАД НИМИ

КЛАССИФИКАЦИЯ БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИН

Варианта {x_n} – переменная величина, которая принимает некоторую последовательность числовых значений.

Определение

Варианта {x_n} – бесконечно малая величина, если для любого ε > 0 существует Nε такое, что для любого n > Nε выполнено : |x_n| < ε.

Иначе : варианта {x_n} – бесконечно малая величина, если, начиная с некоторого достаточно большого номера, |x_n| сколь угодно мал.

Теорема

Сумма и разность двух бесконечно малых величин есть бесконечно малая величина.

Доказательство:

● для суммы

{x_n} – бесконечно малая величина. По определению, для любого ε > 0 существует Nε¹ такое, что

для любого n > Nε¹ выполнено : |x_n| < ε/2

Пусть {y_n} – бесконечно малая величина.

Тогда для этого же ε существует Nε² такое, что для любого n > Nε² выполнено : |y_n| < ε/2

Предположим, что Nε = max {Nε¹, Nε²}

Получим, что для любого ε > 0 существует Nε такое, что для любого n > Nε выполнено :

|z_n| = |x_n + y_n| <= |x_n| + |y_n| <= ε/2 + ε/2 = ε

Следовательно, z_n = x_n + y_n – бесконечно малая величина

● для разности

{x_n} – бесконечно малая величина. Тогда для любого ε > 0 существует Nε¹ такое, что

для любого n > Nε¹ выполнено : |x_n| < 2ε

{y_n} – бесконечно малая величина. Тогда для этого же ε существует Nε² такое, что для любого n > Nε² выполнено : |y_n| < ε

|z_n| = |x_n - y_n| <= |x_n| - |y_n| <= 2ε - ε = ε

Следовательно, z_n = x_n – y_n – бесконечно малая величина.

Теорема

Произведение бесконечно малой величины на ограниченную есть величина бесконечно малая.

Доказательство:

{x_n} – бесконечно малая величина

{y_n} – ограниченная величина

Тогда при любом n |y_n| < M (0 < M, M из R)

Тогда для любого ε > 0 существует Nε такое, что при любом n > Nε : |x_n| < ε/M

Рассмотрим z_n = x_n * y_n

|z_n| = |x_n * y_n| = |x_n| * |y_n| < M * ε/M = ε

Следовательно, z_n = x_n * y_n – бесконечно малая величина

Теорема

Пусть lim x_n = a. Тогда (α_n = x_n – a) – бесконечно малая величина.

Доказательство:

если x_n → a, тогда для любого ε > 0 существует Nε такое, что для любого n > Nε выполнено :

|x_n – a| < ε

|α_n| < ε

Следовательно, α_n – бесконечно малая величина.

Обратно :

пусть x_n = a + α_n, где α_n – бесконечно малая величина.

Тогда для любого ε > 0 существует Nε такое, что для любого n > Nε выполнено :

|α_n| < ε то есть : |x_n - a| < ε

Классификация бесконечно малых величин

Пусть x_n и y_n – бесконечно малые величины

1. если не существует lim (x_n/y_n), то x_n и y_n называют несравнимыми величинами

2. если lim (x_n/y_n) существует и он не равен 0, то величины x_n и y_n одного порядка малости

Обозначение : x_n = O(y_n) или y_n = O(x_n)

3. если lim (x_n/y_n) существует и он равен 1, то величины x_n и y_n эквивалентные

Обозначение : {x_n} ≈ {y_n}

4. если lim (x_n/y_n) существует и он равен 0, то x_n – высшего порядка малости по сравнению с y_n

Обозначение : x_n = o(y_n)

5. если lim (x_n/y_n) существует и он → ∞, то тогда x_n – низшего порядка малости по сравнению с y_n

Обозначение : y_n = o(x_n)

6. если lim (x_n/y_n) существует и он → 1, то тогда x_n – k-ого порядка малости, по сравнению с y_n

7. если x_n → 0, y_n = c/n^k, k > 0, c = const

При n → ∞, y_n → 0.

Если x_n ≈ y_n, то y_n называется главной частью бесконечно малой величины x_n.