Исключение систематических погрешностей

Известные систематические погрешности можно исключить, либо за счет устранения источников погрешностей до начала измерений (профилактика погрешностей), либо путем введения известных поправок в результат измерения в процессе измерения. Профилактика погрешностей является наиболее рациональным спо­собом их снижения. Профилактику погрешностей измерения произ­водят путем регулировки, ремонта и поверки средств измерений. Снизить погрешность измерения можно, устранив влияние колеба­ния температуры (например, термоизоляцией), вибраций и т.п.

Поправка - это значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности. Путем введения поправки исключают, как правило, систематическую постоянную погрешность средств измерений.

При введении поправки уравнение измерения будет иметь вид

y=x+∆_c+∆_n,

где x - значение измеряемой величины;

∆_c - систематическая погрешность измерения;

∆_n - поправка.

Поправка численно равна значению систематической погрешности и противоположна ей по знаку ∆_n = - ∆_c

Полученное при измерении значение величины и уточненное путем введения в него необходимых поправок на действие систематических погрешностей называют исправленным результатом измерения. Неисправленный результат измерения - значение величины, полученное при измерении до введения в него поправок.

Одним из наиболее распространенных методов исключения систематических погрешностей в процессе измерения является метод замещения.

Для реализации этого метода сначала измеряют неизвестную величину (объект измерения размером х), в результате чего получают

х_си=х+∆_с,

где х_си - показания средства измерений.

Ничего не меняя в измерительной системе, устанавливают вместо объекта измерения размером х регулируемую меру (либо меру из набора) с размером х_м, подбирая такое ее значение, при котором достигается прежнее показание средства измерений, тогда

х_си= х_м+∆_c

Сопоставляя равенства получают значение неизвестной величины при х = х_м и определяют значение систематической погрешности

∆_с=х_си-х_м

Пример При измерении диаметра цилиндрической детали штангенциркулем ШЦ-II-0,05 получен результат х_си = 25,75 мм.

Определить поправку, которую необходимо внести в показания прибора, используя набор плоскопараллельных концевых мер длины.

Такой же результат (25,75мм) получают при измерении штангенциркулем блока концевых мер размером х_м = 25,65 мм. Тогда х = 25,65 мм;

а систематическая погрешность штангенциркуля соста­вит, мм:

∆_с = 25,75 - 25,65 = 0,1мм.

Таким образом, поправка, которую необходимо ввести в пока­зания штангенциркуля, мм:

∆_n = -∆_с = -0,1мм.

Универсальным методом исключения неизвестных постоянных систематических погрешностей является метод рандомизации. Суть этого метода заключается в том, что одна и та же величина измеря­ется различными методами (приборами). Систематические погреш­ности каждого из них для всей совокупности являются различными случайными величинами. Вследствие этого при увеличении числа используемых методов (приборов) систематические погрешности взаимно компенсируются.

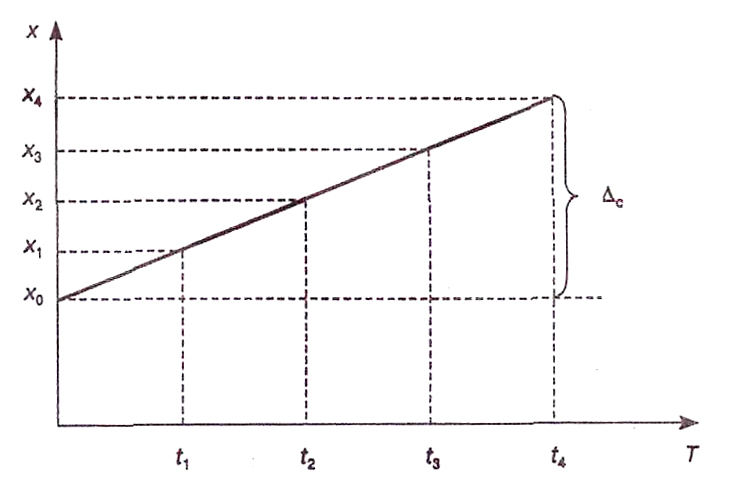
Одним из наиболее простых способов обнаружения и устране­ния переменных систематических погрешностей является графиче­ский метод, который заключается в построении графика последова­тельности неисправленных значений результатов единичных измерений. Расположение полученных точек позволяет обнаружить наличие закономерного изменения результатов измерений и сделать вывод о присутствии в них систематической погрешности.

На рисунке представлено несколько однократных измере­ний постоянной величины х₀, выполненных через равные проме­жутки времени. Если закон изменения систематической погрешности близок к линейному, то графический метод обеспечивает практиче­ски полное ее исключение.