13.4.4. Усилия и моменты в винтовой паре
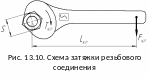
Силы и моменты, возникающие в винтовой (резьбовой) паре, рассмотрим при завинчивании гайки (или винта с головкой) гаечным
ключом (рис. 13.10).
Усилие
,
прикладываемое к рукоятке ключа, создает
момент затяжки (вращающий момент на
ключе):
,
где
— длина ключа (рис. 13.10).
Момент
затяжки
расходуется на
преодоление момента
сил трения в резьбе
и момента
сил трения на опорном торце гайки:
(13.3)
В процессе затяжки
под действием момента
в стержне винта возникает осевая сила
— сила затяжки.
Для установления соотношений между силами и моментами в резьбовом соединении рассмотрим модель, в которой гайка заменена ползуном А, движущимся по винтовой линии (рис. 13.11, а).
Развернем винтовую
линию по среднему диаметру
в наклонную плоскость, по которой
движется ползун А
(рис. 13.11, б)
под действием движущей окружной силы
.
Гайка-ползун воздействует на винт силой
,
нормальной к поверхности витка резьбы
(рис. 13.11, в).
На основном виде (рис. 13.11, а) в натуральную
величину видна проекция вектора силы
,
равная
.
Вектор этой силы перпендикулярен к
направлению витка резьбы (рис. 13.11, б).
192
Рис. 13.11. Силы взаимодействия и момент сил
трения в резьбе при завинчивании гайки
При движении
гайки-ползуна возникает сила трения
,
где
— коэффициент трения
фрикционной пары винт-гайка. Сумма сил
и
дает
результирующую
.
Из треугольника сил имеем (рис. 13.11, б, в):
;
.
Обозначим
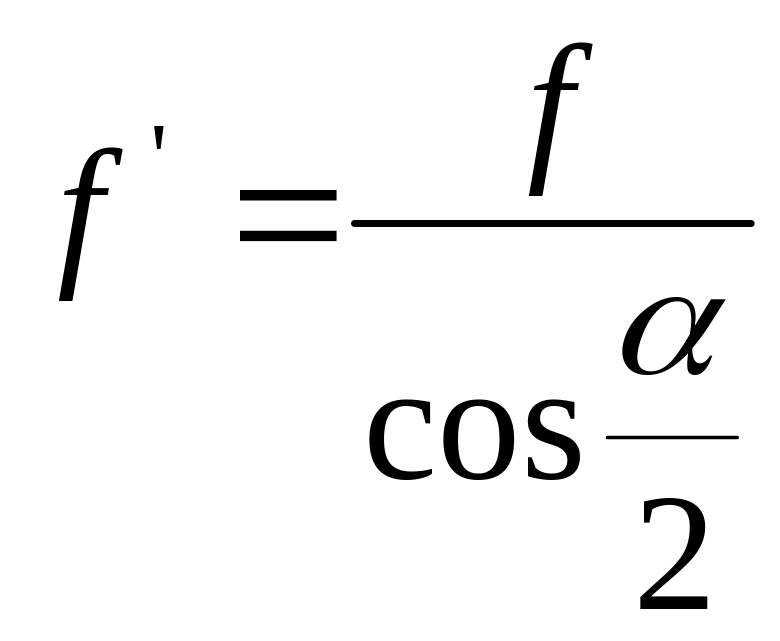— приведенный коэффициент трения в
резьбе. С учетом этого получим
.
С другой стороны из треугольника сил
найдем
,
следовательно
,
или можем записать окончательно
,
здесь
— угол трения в
резьбе.
193
Выразим движущую окружную силу через осевую силу затяжки . Для этого из треугольника сил (рис. 13.11, б) найдем:
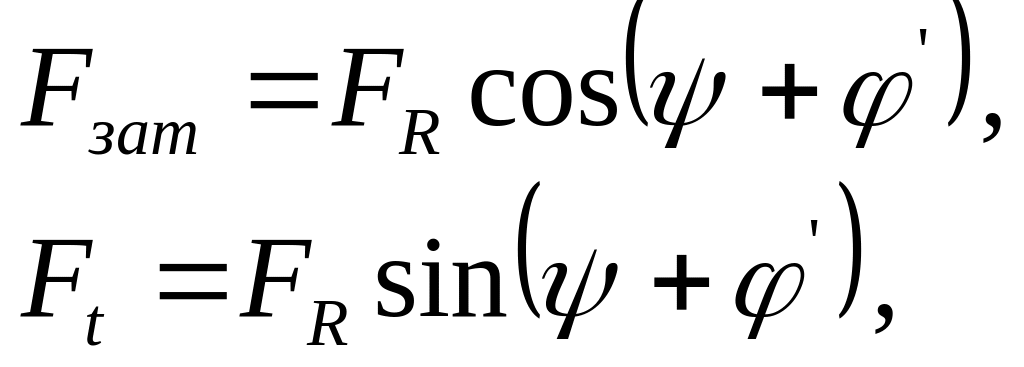
откуда получим соотношение
.
С учетом этого определяют момент сил трения в резьбе при завинчивании гайки
. (13.4)
Возникающий при
завинчивании момент трения в резьбе
скручивает стержень
винта, т.е. создает касательные напряжения.
Найдем
момент сил трения в резьбе при отвинчивании
гайки.
Рассмотрим ту же схему, что и при
завинчивании, но теперь ползун
движется в обратную сторону (рис. 13.12).
С учетом того, что в этом случае силы
и
меняют
свое направление, будем иметь:
.
Рассмотрим условие
самоторможения резьбовой (винтовой)
пары, при котором гайка будет удерживаться
от отвинчивания силами трения. Для этого
необходимо, чтобы момент в резьбе при
отвинчивании был
,
т.е.
.
Это возможно в случае, когда
,
т.е. угол трения в резьбе должен быть больше угла подъема резьбы.
194
Все крепежные резьбы выполняют как самотормозящими, так и несамотормозящими.
Момент сил трения
на торце
гайки
вычисляют, принимая, что равнодействующая
сил трения приложена по среднему диаметру
кольцевой опорной поверхности гайки
.
За наружный диаметр этого кольца
принимают размер под ключ «
»,
за внутренний диаметр — отверстие под
винт
(см. рис. 13.9, а).
С учетом этого получим:
, (13.5)
где
— коэффициент трения на торце гайки.
Подставляя выражения (13.4) и (13.5) в (13.3) найдем
.
195