7.5. Расчет зубьев конических передач на прочность при изгибе

Расчет сводится к расчету на прочность эквивалентного цилиндри­ческого зубчатого колеса. При этом учитывается, что реальное кониче­ское колесо может передать лишь 0,85 нагрузки эквивалентного цилинд­рического зубчатого колеса.

Для прямозубого цилиндрического колеса имеем

. (7.5)

Параметры цилиндрического колеса, эквивалентного коническому зубчатому колесу: ; ; ; .

Подставив параметры эквивалентного цилиндрического колеса в со­отношение (7.5), получим формулу проверочного расчета

. (7.6)

Найдем соотношение для проектировочного расчета. Для, этого выразим , и подставив в соотношение (7.6), получим формулу проектировочного расчета

100

.

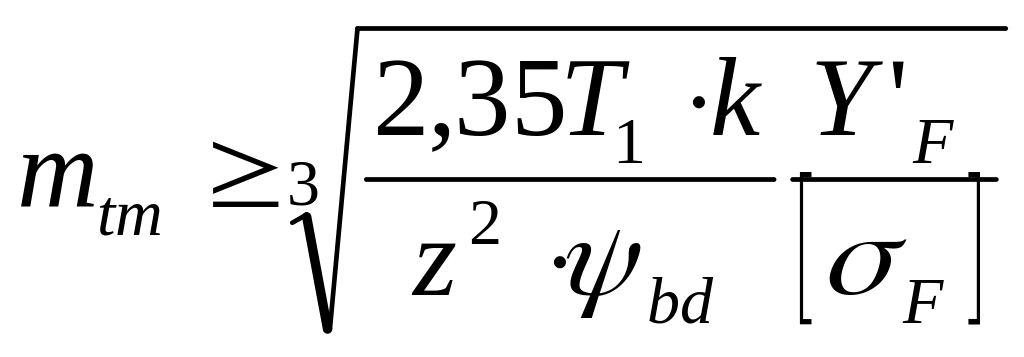Если шестерня и колесо изготавливают из разного материала или из материала с большой разницей в твердости, то расчет на изгибную выносливость ведется для того колеса, у которого отношение будет больше.

Тема 8 проверочный расчет зубчатых передач на статическую прочность при перегрузках

При малом числе циклов переменных напряжений, например, при перегрузках, возникающих при запуске или при переключениях режима работы, и т. п., производится проверка передачи на статическую прочность по пиковым малоцикловым нагрузкам для предотвращения остаточных деформаций или хрупкого излома.

1. Проверка по контактным напряжениям. Производится из условия обеспечения , где — контактные напряжения, вы­зываемые пиковой нагрузкой, — допускаемые контактные напря­жения для условий приложения пиковых малоцикловых нагрузок.

, где — максимальный (пиковый) кратковременно действующий крутящий момент на валу, — номинальный (дли­тельно действующий) крутящий момент. — рабочее контактное напряжение на поверхности зуба шестерни, обу­словленное номинальной нагрузкой.

101

Допускаемое напряжение зависит от термообработки и химико-термической обработки. МПа для нормализованных, улучшенных и объемно-закаленных сталей; МПа для цементованных и поверхностно-закаленных сталей.

2. Проверка зубчатых передач по изгибным напряжениям. Производится из условия , где — напряжения изгиба, обусловленные пиковой нагрузкой, — допускаемое напряжение изгиба для условий приложения пиковых нагрузок.

зависит от термообработки:

при ,

при ,

здесь — предел текучести материала зубчатого колеса.

Данную проверку выполняют для зубьев шестерни и колеса в отдельности.

102

Лекция 7

Тема 9 другие виды передач зацеплением

9.1. Планетарные передачи

Планетарными называется передачи, имеющие зубчатые колеса с перемещающимися геометрическими осями. Движение этих колес, называемых сателлитами, аналогично движению планет вокруг Солнца. Поэтому эти передачи получили название планетарных. Разработано большое число схем планетарных передач. Одна из простых и распространенных планетарных передач (рис. 9.1) состоит из вращающегося центрального колеса a с наружным зацеплением, неподвижного центрального колеса b с внутренним зацеплением и водила h, на котором закреплены оси сателлитов g. Центральное колесо a называют солнечным, другое колесо b- корончатым. Сателлиты g совершают планетарное движение, т.е вращаются вокруг своих осей и вокруг колеса a. При неподвижном колесе b движение может передаваться от колеса a к водилу h и наоборот. При неподвижном водиле h и подвижном колесе b получается простая зубчатая передача.

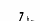
Рис. 9.1. Схема планетарной передачи

103

Если в планетарной передаче подвижны оба центральных колеса и водило, то такую передачу называют дифференциальной. Она имеет две степени подвижности. Наиболее распространены передачи, в которых одно из центральных колес закреплено, тогда механизм обладает лишь одной степенью свободы (рис.9.1). Для определения передаточных отношений планетарных механизмов применяют принцип обращения движения. Он состоит в том что всему механизму задают (мысленно) вращение с частотой- равной по величине и противоположной по направлению частоте вращения водила h). Тогда водило h рассматривается как неподвижное, а весь механизм- как простая зубчатая передача.

Рассмотрим схемы наиболее распространенных передач 2К-h (обозначение 2К определяет наличие двух центральных колес a и b и водила h), изображенных в табл. 9.1

Схема 1 представляет собой простейшую одноступенчатую планетарную передачу. Такая передача наиболее распространена благодаря высокому КПД и технологичности. Схема 2 используется при больших передаточных числах. Она включает две ступени, каждая из которых выполнена по схеме 1. Возможно также использовать передачи и с большим числом ступеней. Схема 3 близка к схеме 1, но на водиле установлен блок с двухрядным сателлитом. Эта передача более сложная и требует изготовления с повышенной точностью. Диапазон передаточных чисел этих передач выше передач, выполненных по схеме 1, а масса меньше двухступенчатых передач по схеме 2.

Планетарные передачи относятся к передачам соосной схемы и обычно являются многопоточными (двух, трех и более, в зависимости от количества сателлитов) благодаря чему снижаются нагрузки на зубья и уменьшаются размеры колес и передачи в целом. Расчет на прочность планетарных передач выполняют по формулам для цилиндрических передач. Широкое применение планетарные передачи находят на транспорте, в станкостроении, приборостроении, в аэрокосмической технике и других отраслях промышленности.

104

Номер схемы	Схемы передач	Передаточное число	КПД
1
2
3

Таблица 9.1 – Схемы планетарных передач

105

Основными достоинствами планетарных передач являются: меньшие габаритные размеры и масса, так как вращающий момент передается по нескольким потокам; большие передаточные числа в одной ступени; меньшие поперечные (радиальные) силы, приходящие на валы. Однако планетарные передачи требуют повышенной точности изготовления (не ниже седьмой степени точности); более сложны в сборке; при больших передаточных числах резко снижается их КПД.