
- •Тема 5 зубчатые передачи………………………………………………………54
- •Тема 6 цилиндрические зубчатые передачи……………………..62
- •Тема 6 цилиндрические зубчатые передачи……………………..77
- •Тема 7 конические зубчатые передачи……………………………….90
- •Тема 12 опоры валов и осей……………………………………………….151
- •Тема 12 опоры валов и осей……………………………………………….167
- •Тема 13 соединения деталей машин…………………………………….174
- •Тема 13 соединения деталей машин………………………………..185
- •Тема 13 соединения деталей машин………………………………..196
- •Тема 13 соединения деталей машин………………………………..210
- •Тема 13 соединения деталей машин………………………………..224
- •Предисловие
- •1.2. Общая классификация деталей и узлов машин
- •1.3. Основные требования, предъявляемые
- •Лекция 2
- •Тема 3 критерии работоспособности и расчета деталей машин
- •3.1. Прочность
- •3.2. Жесткость
- •3.3. Статическая устойчивость
- •3.4. Виброустойчивость
- •3.5. Износостойкость
- •3.6. Термостойкость
- •4.2. Кинематические и энергетические соотношения в механических передачах
- •Тема 5 зубчатые передачи
- •5.1. Общие сведения, преимущества и недостатки
- •Зубчатых передач
- •5.2. Классификация зубчатых передач
- •5.3. Основные требования к зубчатому зацеплению. Эвольвента и её свойства. Понятие о нарезании зубьев
- •5.4. Основные геометрические параметры эвольвентного зацепления
- •5.5. Точность зубчатых передач
- •5.6. Усилия в зацеплении зубчатых передач
- •5.7. Условия работы зуба в зацеплении. Напряжения в элементах зуба
- •5.8. Расчетная нагрузка в зацеплении
- •5.9. Виды повреждений зубьев. Критерии работоспособности и расчета зубчатых передач
- •5.11. Материалы зубчатых колес
- •Тема 6 циллиндрические зубчатые передачи
- •6.1. Элементы геометрии прямозубого цилиндрического
- •6.2. Особенности геометрии косозубых цилиндрических колес
- •6.3. Коэффициенты перекрытия
- •6.4. Понятие об эквивалентном зубчатом колесе
- •6.6. Расчет косозубых цилиндрических передач
- •6.7. Расчет зубьев прямозубых цилиндрических передач
- •6.8. Расчет зубьев косозубых цилиндрических передач
- •Лекция 6
- •Тема 7 конические зубчатые передачи
- •7.1. Общие сведения
- •7.2. Геометрические параметры конических зубчатых передач
- •7.3. Распределение нагрузки по длине зуба конического колеса. Приведение конического колеса к эквивалентному цилиндрическому
- •7.4. Расчет конических зубчатых передач на контактную прочность
- •7.5. Расчет зубьев конических передач на прочность при изгибе
- •Тема 8 проверочный расчет зубчатых передач на статическую прочность при перегрузках
- •Лекция 7
- •Тема 9 другие виды передач зацеплением
- •9.1. Планетарные передачи
- •9.2. Волновые передачи
- •9.3. Передачи винт-гайка
- •9.4. Червячные передачи
- •Тема 10
- •10.2. Геометрия, кинематика и силы в ременной передаче
- •10.3. Виды повреждений, критерии работоспособности и применяемые материалы ременных передач
- •10.4. Расчет ременной передачи
- •Тема 11 валы, оси и муфты
- •11.1. Назначение, классификация и конструктивные
- •Особенности валов и осей
- •11.2. Виды повреждений валов и осей, критерии работоспособности и применяемые материалы
- •11.3. Нагрузки и расчетные схемы валов и осей
- •Лекция 9
- •Тема 11 валы, оси и муфты
- •11.4. Расчёт валов и осей на прочность
- •11.5. Муфты для соединения валов
- •11.5.1. Назначение, конструкция и классификация муфт
- •11.5.2 Подбор стандартных муфт
- •11.5.3 Расчёт нестандартных муфт
- •Лекция 10
- •Тема 12 опоры валов и осей
- •12.1. Подшипники скольжения
- •12.1.1. Конструкция, материалы, достоинства и недостатки подшипников скольжения
- •12.1.2. Виды повреждений и критерии работоспособности подшипников скольжения
- •12.1.3. Условия работы и расчет подшипников скольжения
- •12.2. Подшипники качения
- •12.2.1. Конструкция, материалы, достоинства и недостатки, классификация подшипников качения
- •12.2.2. Распределение нагрузки между телами качения. Напряжения и деформации в подшипниках качения
- •12.2.3. Кинематика и потери на трение в подшипниках качения
- •Лекция 11
- •Тема 12 опоры валов и осей
- •12.2.4. Виды повреждений и критерии работоспособности подшипников качения
- •12.2.5. Выбор и расчет подшипников качения
- •Тема 13 соединения деталей машин
- •13.1. Основные понятия и общая классификация соединений
- •13.2. Шпоночные соединения
- •13.3. Шлицевые (зубчатые) соединения
- •13.4.2. Основные повреждения и критерии работоспособности, материалы и классы прочности резьбовых деталей
- •13.4.3. Распределение нагрузки по виткам резьбы. Стандартные соотношения элементов резьбовых деталей
- •13.4.4. Усилия и моменты в винтовой паре
- •Лекция 13
- •Тема 13 соединения деталей машин
- •13.4.5. Расчёт резьбовых соединений на прочность при постоянных нагрузках
- •Расчёт затянутого (напряжённо-
- •13.4.6. Расчёт резьбовых соединений на прочность при переменных нагрузках
- •13.4.7. Определение допускаемых напряжений при расчёте резьбовых соединений и основные мероприятия по повышению их сопротивления усталости
- •13.4.8. Расчёт групповых резьбовых соединений
- •Тема 13
- •13.5.2. Дефекты сварных соединений, критерии их работоспособности и допускаемые напряжения
- •13.5.3. Расчет стыкового сварного шва
- •13.5.4. Расчет углового (валикового) сварного шва
- •13.5.5. Способы повышения прочности и сопротивления усталости сварных швов
- •Тема 13
- •13.6.2. Элементы геометрии заклепочного соединения
- •13.6.3. Виды повреждений и критерии работоспособности заклепочных соединений
- •13.6.4. Проверка прочности элементов заклепочного соединения
- •13.6.5. Расчет заклепочного шва
- •13.6.6. Допускаемые напряжения при расчете заклепочных соединений
6.2. Особенности геометрии косозубых цилиндрических колес
Геометрия косозубых колес отличается тем, что зубья расположены под углом β к образующей начального цилиндра (рис.6.4) Это обусловливает следующие преимущества - значительное снижение динамических нагрузок , шума и вибраций, следовательно, существенное повышение несущей способности косозубых колес по сравнению с прямозубыми.
Недостатки –
сложность шлифования закаленных
косозубых колес и повышенная осевая
сила на опоры, обусловленная наклоном
зубьев. Рассмотрим обкатку основного
цилиндра диаметром
![]() плоскостью (рис. 6.5). При обкатке каждая
точка прямой
М-М
опишет эвольвенту, а вся
прямая – боковую
поверхность косого зуба. Геометрию
косозубого колеса рассматривают в
торцевом сечении L-M
или AB
и в нормальном
к направлению зуба сечении БВ.
плоскостью (рис. 6.5). При обкатке каждая
точка прямой
М-М
опишет эвольвенту, а вся
прямая – боковую
поверхность косого зуба. Геометрию
косозубого колеса рассматривают в
торцевом сечении L-M
или AB
и в нормальном
к направлению зуба сечении БВ.
67
Рассмотрим зацепление в торцевом сечении, например, AB (рис. 6.6.)
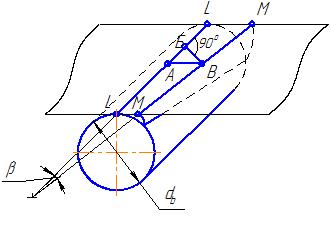
Рис 6.5. Схема образования косого зуба
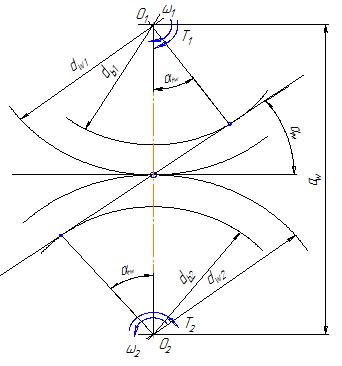
Рис. 6.6. Схема косозубого зацепления в торцевом сечении
68
Профиль косого зуба в нормальном сечении, например БВ (см. рис. 6.5), совпадает с профилем прямого зуба. В торцевом сечении, например АВ, параметры косого зуба изменяются в зависимости от угла наклона β. Для косозубых колес различают нормальный шаг Pn , измерений, например в сечении БВ (см. рис. 6.4 и 6.5), нормальном к направлению зуба и торцевой шаг Pt , измеренный, например в сечении АВ, перпендикуляром к оси колеса.
Очевидно (см. рис. 6.4 и 6.5), что Pt = Pn /сos β. Отсюда получим
![]() - нормальный модуль
( в нормальном сечении),
- нормальный модуль
( в нормальном сечении),
![]() =
Pn
/(
=
Pn
/(![]() -
торцовый модуль (окружной).
-
торцовый модуль (окружной).
Нормальный модуль mn стандартизован и совпадает с модулем для прямозубых цилиндрических колес, поэтому нарезка зубьев косозубых колес осуществляется тем же инструментом, что и прямозубых, только повернутым на угол β относительно оси колеса.
Все размеры косозубых колес выражаются через нормальный модуль mn . По аналогии с прямозубыми колесами имеем:
высота головки
зуба
![]()
высоты ножки
зуба
![]()
высота зуба
![]()
диаметр делительной окружности
![]()
межосевое расстояние
![]()
69
делительное межосевое расстояние
![]()
коэффициент смещени
![]()
суммарный коэффициент смещения
![]()
коэффициент воспринимаемого смещения
![]()
коэффициент уравнительного смещения
![]()
диаметр выступов
![]()
диаметр впадин
![]()
угол профиля зуба в торцевом сечении (рис. 6.7)
![]()
где
![]() -
угол профиля в нормальном сечении,
-
угол профиля в нормальном сечении,
![]()
аналогично, как для прямозубых колес.
угол зацепления
![]() в
торцевом сечении (см.рис. 6.6)
в
торцевом сечении (см.рис. 6.6)
![]()
70
аналогично, как для прямозубых колес.
угол зацепления в торцевом сечении (см.рис. 6.6)
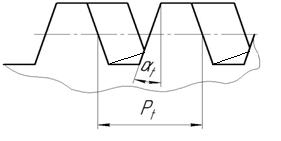
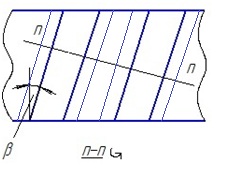
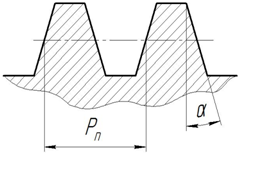
Рис. 6.7. К понятию об углах профиля в торцевом и нормальном сечения
71
