5.7. Условия работы зуба в зацеплении. Напряжения в элементах зуба

При передаче вращающего момента Т в зацеплении кроме нормальной силы F_n возникает сила трения ( — коэффициент трения), связанная со скольжением профилей зубьев (рис. 5.8). И только в полюсе Р сила исчезает, так как в указанной точке, согласно теории зацепления, имеет место чистое качение, т.е. качение без скольжения.

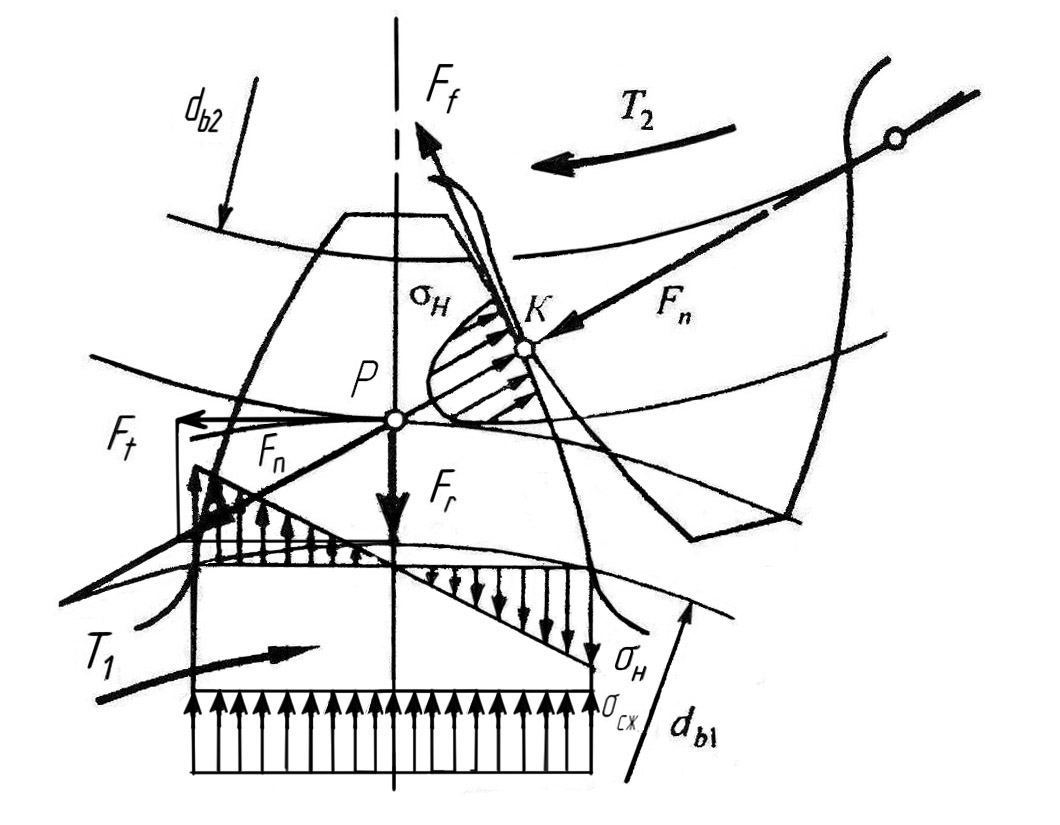
Рис. 5.8. Напряжения, возникающие в зубьях

46

В результате силового взаимодействия профилей (рис. 5.6) первоначальный контакт зубьев по линии вследствие деформации превращается в площадку малых размеров, при этом каждое очередное нагружение зуба вызывает в нем сложное напряженное состояние (рис. 5.8): в зоне контакта под действием силы нормального давления F_n возникают контактные напряжения , т.е. такие напряжения, которые действуют на площадке касания двух тел в случае, когда размеры площадки существенно меньше размеров тел; сила трения обусловливает появление тангенциальных напряжений ; результатом действия окружного и радиального усилий являются напряжения изгиба и сжатия .

Все напряжения, действующие на зуб при работе, являются переменными. Они изменяются во времени по некоторому прерывистому пульсирующему циклу. Решающее значение на работоспособность зуба оказывают два основных напряжения: контактные напряжения и напряжения изгиба у корня зуба, где величина их максимальна.

Решение контактной задачи впервые получили немецкий физик Г.Герц из рассмотрения общего случая контакта двух тел. При сжатии двух цилиндров с параллельными осями (рис. 5.9) на основе решения этой задачи получено, что в поперечном сечении по площадке контакта напряжения изменяются по эллиптическому закону, достигая максимального значения в зоне максимальных деформаций — по линии действия прижимающей силы F_n (см. элемент А на рис. 5.9).

Максимальное значение используют в качестве основного критерия контактной прочности (индекс «max» при этом опускают):

,

где — допускаемое контактное напряжение, получаемое из

эксперимента или опыта эксплуатации при аналогичных условиях в

47

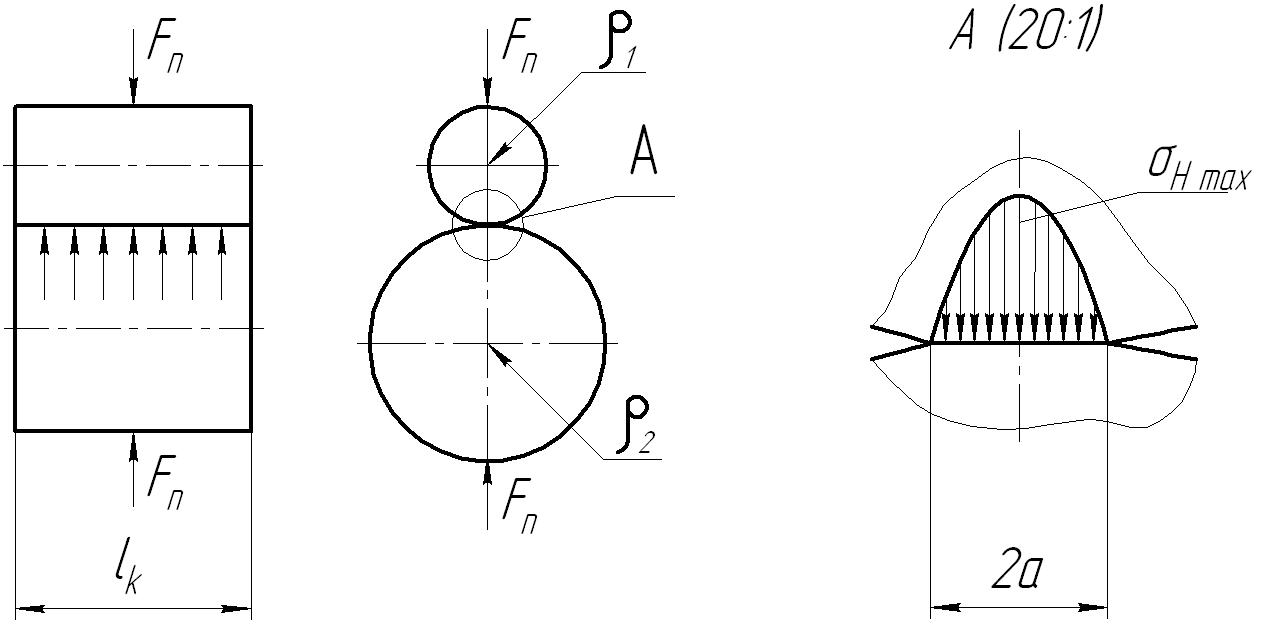
Рис. 5.9. Схема сжатия двух цилиндров с параллельными

осями и распределение напряжений на площадке контакта

зоне контакта. Напряжения определяют аналитически. На основе решения Герца формула для расчета максимальных контактных напряжений в центре площадки контакта имеет вид:

, (5.1)

где — удельная нагрузка, — сжимающая сила, — длина линии контакта (длина цилиндров); — коэффициент, учитывающий упругие свойства материалов контактирующих тел; и — соответственно коэффициенты Пуассона и модули упругости материалов; — приведенный радиус кривизны для контактирующих цилиндров с радиусами кривизны и ; здесь знак «+» для контакта двух выпуклых поверхностей, знак «—» для контакта выпуклой и вогнутой поверхностей.

48

5.8. Расчетная нагрузка в зацеплении

В зубчатом зацеплении при работе передачи кроме номинальной нагрузки возникают дополнительные нагрузки из-за ошибок изготовления деталей, их деформаций и условий эксплуатации. В расчетах это учитывают умножением номинальной силы F_n или момента T на коэффициент нагрузки K, определяя тем самым расчетную нагрузку:

и

Расчетная удельная нагрузка на зуб определяется по зависимости

,

где — суммарная длина линий контакта; для косозубых передач , — коэффициент торцового перекрытия, — ширина зубчатого венца; для прямозубых передач ; — нормальная сила в зацеплении. Так как , , то

.

При расчете по контактным напряжениям коэффициент нагрузки

.

При расчете по напряжениям изгиба коэффициент нагрузки

.

Здесь — коэффициент, учитывающий внешнюю динамическую нагрузку передачи при совместной работе с двигателем и исполнительным звеном ( ≥ 1). = 1, если динамическая внешняя нагрузка учтена в циклограмме нагружения.

49

— коэффициенты, учитывающие неравномерность распределения нагрузки между зубьями, определяется точностью изготовления колес и погрешностями в окружном шаге между зубьями. Для однопарного зацепления (цилиндрические прямозубые передачи) коэффициент не учитывают.

— коэффициенты концентрации нагрузки, учитывающие неравномерность распределения нагрузки по длине контактных линий; возникает вследствие ошибок направления зубьев, упругих деформаций зубьев, валов и их опор.

— коэффициенты внутренней динамической нагрузки, учитывающие степень точности передачи по нормам плавности (погрешности основных шагов зубьев) и окружную скорость.

Численные значения коэффициентов и приведены в справочной литературе в виде таблиц или графиков.