Лекция 11a. Классы

Классы – это типы данных похожие на структуру в языке С++ или запись в языке Pascal.

Синтаксис объявления класса (для C++):

class <имя класса ><список- классов-родителей>

{

public: // доступно всем

<данные, метки, свойства, события>

protected: // доступно только потомкам

<данные, метки, свойства, события>

private: // доступно только в классе

<данные, метки, свойства, события>

}

public, protected, private – это разделы класса.

В каждом разделе также как в структуре можно определять данные различных типов. Их называют свойствами, полями. Кроме того, можно определять имена вызываемых функций (для Delphi процедур и функций). Это методы класса. Для каждого класса существуют специальные методы: конструкторы и деструкторы. Имя конструктора совпадает с именем класса.

Три “кита” объектного программирования:

• Инкапсуляция;

• Полиморфизм:

• Наследование.

Инкапсуляция – это объединение данных и программ обработки этих данных. Комбинирование записей с процедурами и функциями, манипулирующими полями этих записей, формирует новый тип данных – объект.

Классическое правило объектно-ориентированного программирования утверждает, что для обеспечения надежности нежелателен прямой доступ к полям объекта: чтение и обновление их содержимого должно производиться посредством вызова соответствующих методов. Это правило называется инкапсуляцией.

Отличие свойства от поля: свойству соответствуют два метода для чтения и записи. Внешне свойство выглядит так же, как поле. Свойство – это поле + 2 метода для чтения и записи.

Полиморфизм означает, что много классов могут обеспечивать одинаковые свойства или методы, и при обращении к объекту обращающийся метод или процедура не обязаны знать, к какому классу объект принадлежит.

Наследование – это простой принцип, означающий, что если вы хотите создать новый класс, лишь немного отличающийся от старого, то совершенно нет необходимости в переписывании заново уже существующих полей и методов. Просто объявляем, что новый класс является дочерним классом старого класса, называемого предком или родительским классом и добавляем к нему новые поля методы и свойства.

Пример (Visual C++)

class CaboutDlg: public CDialog

{

private:

long m_dwRef;

public:

CaboutDlg ();

enum {IDD = IDD_ABOUTBOX};

protected:

virtual void DoDataExchange (char * pDX);

};

Лекция 12. Графы

Несколько определений

Прямое произведение X на Y это множество пар (x, y), где x принадлежит X, а у принадлежит Y. Оно обозначается X ^x Y.

Отношение между множествами X и Y – это любое подмножество X ^x Y (прямое произведение X на Y).

Функция – это отношение специального вида.

Граф описывает отношение некоторого множества к самому себе.

Ориентированный граф – это система G = (X,U), где X – это множество элементов, называемых вершинами или точками, а U – определенное на множестве X отношение (т. е. U – подмножество X ^x Y). Элементы U называются дугами или ребрами графа. Если a и b –вершины, а (a,b) – ребро, говорят, что это ребро направлено из вершины a в вершину b.

Неориентированный граф – это граф, в котором отсутствует ориентация ребер. Это можно описать следующим образом: (a,b) принадлежит U тогда и только тогда, когда (b,a) принадлежит U.

Представление ориентированного графа в виде рисунка. G= ({a,b,c,d}, {(ab), (b,c), (c,d), (d,a), (b,d), (d,c) }).

Представление графа с помощью матрицы смежности.

	a	b	c	d
a	0	1	0	0
b	0	0	1	1
c	0	0	0	1
d	1	0	1	0

Представление графа с помощью матрицы инцидентности (или операторное представление графа).

x, принадлежащее X	Отношение U(x)
a	{b}
b	{c,d}
c	{d}
d	{a,c}

Граф называется регулярным, если из каждой его вершины выходит одно и то же число ребер и в каждую его вершину входит одно и то же число ребер.

Две вершины графа связаны, если существует путь от одной из них до другой.

Граф называется слабо связным, если все пары вершин связаны без учета ориентации.

Граф называется сильно связным, если все пары вершин связаны с учетом ориентации.

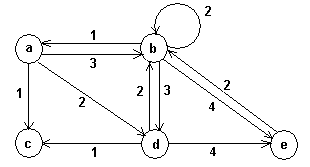
Граф с помеченными ребрами

Представление графа с помощью матрицы инцидентности

	1	2	3	4
a	c	d	b
b	a	b	d	e
c
d	c	b		e
e		b

Представление графа с помощью матрицы смежности.

	a	b	c	d	e
a	0	1	1	1	0
b	1	1	0	1	1
c	0	0	0	0	0
d	0	1	1	0	1
e	0	1	0	0	0