Лекция 8. Основные понятия рекурсии. Простейшие примеры реализации.

Объект называется рекурсивным, если он частично состоит или частично определяется через самого себя.

Примеры рекурсивных определений

1. Деревья:

   1. 0 есть дерево (его называют пустым деревом)

   2. если t1 и t2 - деревья, то построение, содержащее вершину с двумя ниже расположенными деревьями, тоже дерево.

2. Факториал (n!):

1. 0! = 1

2. n > 0 : n! = n * (n-1)!

3. Числа Фибоначчи:

   1. a₀ = 1; a₁ = 1

   2. i>1 : a_i = a_i-1 + a_i-2

Рекурсивное определение позволяет с помощью конечного высказывания определить бесконечное множество объектов.

Рекурсивную программу P можно определить, как некоторую композицию P из множества операторов S (не содержащих P) и самой P:

P = P[S,P]

Если процедура P содержит явную ссылку на саму себя, то ее называют прямо рекурсивной.

Если процедура P ссылается на процедуру Q, содержащую ссылку на P, то P называют косвенно рекурсивной.

Также как операторы цикла, рекурсивные процедуры могут приводить к бесконечным вычислениям. Для того, чтобы рекурсивная процедура P когда-нибудь завершилась, необходимо, чтобы рекурсивное обращение к P когда-нибудь перестало происходить. Для этого необходимо, чтобы рекурсивное обращение к P зависело от некоторого условия, которое в какой-то момент перестает выполняться. Отсюда вытекают такие формы рекурсивных алгоритмов:

P = if B then P [S,P]

P = P [S, if B then P]

В практических приложениях важно убедиться , что максимальная глубина рекурсии не только конечна но и достаточно мала, так как может не хватить памяти на сохраняемые переменные и текущее состояние вычислений.

Когда не надо применять рекурсию.

Некорректное использование рекурсии происходит тогда, когда в рекурсивной процедуре к ней же обращаются несколько раз. При этом получается сильно ветвящееся дерево из рекурсивных процедур. Это приводит к тому, что быстро исчезает память.

В блоке 8 рассматривается пример вычисления чисел Фибоначчи. Каждое обращение к процедуре приводит еще к двум обращениям и число их растет экспоненциально. Поэтому в таких случаях лучше применять итеративную схему.

// Рекурсивная функция для вычисления числа Фибоначчи

Function Fib(n:integer):integer;

begin

if n=0 then result:= 0

else if n=1 then result:= 1

else result:= Fib(n-1) + Fib(n-2);

end;

Лекция 9. Рекурсия и кривые. Рекурсивная реализация

Ниже на рисунке изображены кривые Гильберта первого, второго и третьего порядков H1, H2, и H3. Hi+1 получается соединением четырех экземпляров Hi вдвое меньшего размера, повернутых соответствующим образом и “стянутых” вместе тремя прямыми отрезками. H1 можно считать получается из пустой H0. Эти четыре части обозначим A, B, C, D. Стрелками обозначим процедуры, рисующие соединительные кривые. Схема рекурсий и вид кривых приведены ниже на рисунке.

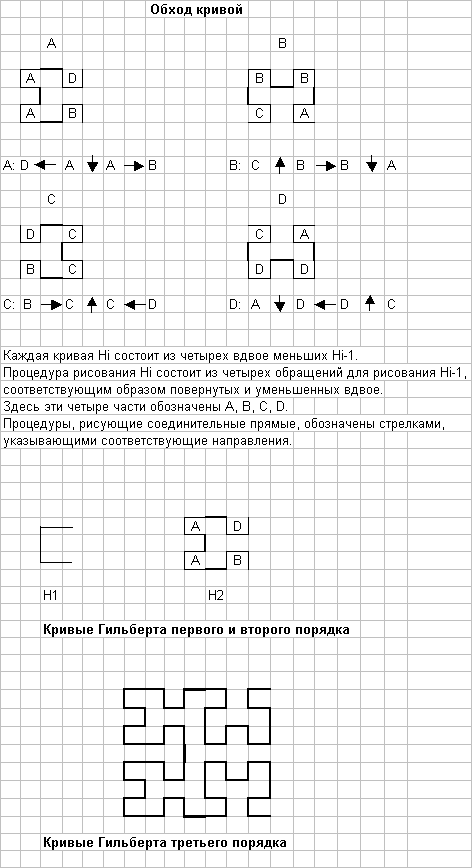
Лекция 10. Алгоритмы с возвратом.

Тема 3.3. Алгоритмы с возвратом.

Алгоритмы, ищущие решения методом проб и ошибок. Задача о ходе коня. Схема выполнения.

В задачах искусственного интеллекта мы имеем дело с алгоритмами, ищущими решение не по заданным правилам, а путем проб и ошибок. Часто процесс поиска путем проб и ошибок можно разделить на ряд задач, которые решаются рекурсивнымии методами и обращаются к конечному числу подзадач.

Задача. В качестве примера рассмотрим задачу о ходе коня.

Дана доска размером n x n. На поле с координатами x0, y0 находится конь. Надо найти последовательность ходов, если она существует, при которой конь точно один раз побывает на всех полях доски.

Ниже изображена схема процедуры.

Procedure sledhod; // следующий ход

Begin

Инициализация выбора хода

repeat выбор очередного кандидата из списка ходов

if подходит then begin

Запись хода

if доска не заполнена then begin

sledhod;

if неудача then begin уничтожение предыдущего хода end;

end;

end;

until удача or кандидатов больше нет

end;

Задача о ходе коня. Схема выполнения.

• Доска из n*n клеток. Сначала во все клетки записываем 0.

• На i-ом ходе в соответствующей клетке пишем i

• Условие доска не заполнена при i-ом ходе i < n*n

• При правильном ходе координаты u, v должны удовлетворять отношениям:

1<= u <= n и 1 <= v <= n

• Если ход не подходит, то записываем на его место 0 и ищем другой ход.