21. Биноминальный закон распределения. Мат ожидание и дисперсия св распределенной по биноминальному закону.

Определение: Дискретная св Х имеет биноминальный закон распределения, если она принимает знач 0,1,2…, m,…, n с вероятностями P(X=m)= , где 0<p<1, q=1 – p, m=0,1,…,n. Следовательно биноминал закон распределения представляет собой закон распределения X=m наступления события А в n независимых испыт, в каждом из которых оно может произойти с одной и той же вероятностью p. Теорема. Математическое ожидание числа появлений события в независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании, которая вычисляется по формуле: M(X)=np. Теорема. Дисперсия числа появлений события в независимых испытаниях равна произведению числа испытаний на вероятности появления и не появления события в одном испытании: Д(Х)=npq.

22. Закон распределения Пуассона. Мат ожидание и дисперсия св, распределенной по закону Пуассона.

Определение: дискретная св Х имеет закон распределения Пуассона, если она принимает значения 0,1,2, … , m, … (бесконечное, но счетное множество значений) с вероятностями P(X=m)= , где m=0,1,2, …; . Теорема. Мат ожидание и дисперсия св, распределенной по закону Пуассона, совпадают и равны параметру этого закона, т.е. М(Х)= , Д(Х)= .

23. Равномерный закон распределения. Мат ожидание и дисперсия св, распределенной по равномерному закону.

Определение. Непрерывная св Х имеет равномерный закон распределения на отрезке [ ], если ее плотность (х) постоянна на этом отрезке и равна нулю вне его, т.е.:

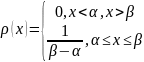
Теорема. Функция распределения св Х, распределенной по равномерному закону, есть:

Ее мат ожидание: , а дисперсия: .

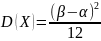24. Показательный закон распределения. Мат ожидание и дисперсия св, распределенной по показательному закону.

Определение. Непрерывная св Х имеет показательный (экспоненциальный) закон распределения с параметром распределения , если плотность вероятности имеет вид:

Теорема. Функция распределения св Х, распределенной по показательному (экспоненциальному) закону имеет следующие вид:

Ее мат ожидание: , а дисперсия: .

Для св, распределенной по показательному закону, мат ожидание равно среднему квадратическому отклонению.

25. Нормальный закон распределения. Мат ожидание и дисперсия св, распределенной по нормальному закону.

Определение. Непрерывная св Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и , если ее плотность вероятности имеет вид: , где а – математическое ожидание, – дисперсия. Кривую нормального закона распределения наз нормальной или гауссовой кривой. Теорема. Мат ожидание св Х, распределенной по нормальному закону, равно параметру а этого закона, а ее дисперсия – Закон положен в связи с разработкой теории ошибок наблюдения. НСВ Х с а=0 и =1 называется стандартной нормальной величиной. Распределение вероятностей нормальной св яв нормальным распределением. Общим наз нормальное распределение с произвольными параметрами а и ( ). Плотность стандартного распределения (табулирована). Функция F(x) общего нормального распределения имеет вид: ,а функция стандартного нормального распределения: . (табулированное значение).

Свойства:

1) вероятность попадания св в интервал от х₁ до х₂ равна:

Р(х₁  Х  х₂)=(Ф(t₂) – Ф(t₁)), где _{, .}

2) вероятность того, что отклонение случайной величины Х, распределенной по нормальному закону, от математического ожидания не превысит величину (по абсолютной величине равна: ).