10.Еріксіз тербелістер. Еріксіз тербеліс фазасы және амплитудасы. Резонанс. Резонанстық қисықтар.

Еріксіз тербелістер – периодты түрде өзгеретін күштің әсерінен пайда болатын тербелістер. Теңдеуін қорытып шығарайық. Сыртқы күш уақыт бойынша гармоникалық заңмен өзгерсін f=F₀cosΩt осымен қатар денеге ортаның кедергі және серпімділік күштері әсер етеді. Ньютонның екінші заңына mx´´=-kx-rx´´+F₀cosΩt ,F₀/m=f₀ белгілесек x´´+2β x´+ɷ₀²х= f ₀cosΩt (1) еріксіз тербелістердің теңдеуін аламыз. Шешімі x= а₀ +𝜑₀) немесе х=а ₀cos(Ωt+𝜑₀) Бұдан бірінші және екінші туындыларын және х шамасы (1) теңдеуге қойсақ а₁ cos(Ωt+𝜑₀₊π)+а₂cos(Ωt+𝜑₀₊π/2)+ а ₃cos(Ωt+𝜑₀)= f ₀cosΩt теңдеуін аламыз, мұндағы а₁=Ω² a, a₂=2βΩa, a₃=ɷ² A . Бұдан бастапқы фазалары әр түрлі үш гармоникалық тербелістердің қосындысы F₀cosΩt тең болуға тиіс a=f₀/

Бұдан еріксіз тербелістің амплитудасы және тепе-теңдігін ығысуы мен сыртқы күштің арасындағы ығысу фазасы сыртқы күштің жиілігіне, меншікті жиілікке және өшу коэффициентіне байланысты.

Х=f₀cos(ɷt-arctg2βΩ/ )/

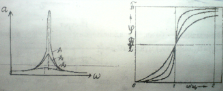
Резонанс – сыртқы күштің жиілігі жүйенің меншікті тербеліс жиілігіне жақындығында ,жүйедегі еріксіз тербелістің амплитудасының мәні кенеттен арту құбылысы.

ɷ_рез=

a_рез=f₀/

11.Толқындық процестер. Бойлық және көлденең толқындар. Толқын теңдеуі. Фазалық жылдамдық, толқын ұзындығы, толқындық сан. Толқын- тербелістің кеңістікте таралу процесі. Толқын тарайтын ортаның бөлшектері толқынмен ілесіп кетпейді, олар өзінің тепе- теідік қалпының маңында ғана тербеледі. Толқын таралатын бағытпен салыстырғандағы бөлшектер тербелістің бағытына байланысты қума және көлденең болып екіге бөлінеді.

Көлденең толқын – ортаның бөлшектері толқынның таралу бағытына перпендикуляр тербеледі.

Қума (бойлық) толқын - ортаның бөлшектері толқынның таралу бағыты бойынша тербеледі.

Бойлық толқын – газ бен сұйықтарда таралатын толқын.

Механикалық көлденең толқындар ығысу кедергісі бар ортада ғана пайда бола алады. Сондықтан сұйық және газ тектес ортада тек қума толқын тарай алады. Уақыт өтуіне байланысты орта бөлшектерінің қозғалысы берілген, әр түрлі бөлшектер фазасы бойынша тербеледі.

Толқын ұзындығы - бірдей фазада ең жақын орналасқан бөлшектердің арақашықтығы. немесе λ= .

Фазалық жылдамдық – фазаның орын ауыстыру жылдамдығы. Толқын фазасы мәнімен анықталады. Берілген фазада барлық нүктедегі тербеліс амплитудасы бірдей болады, олай болса . Осы өрнекті диференциалдай отырып фазалық жылдамдығы табамыз. dt- =0. .

Толқындық сан - 2 ұзындығына қаншалықты толқын ұзындығы сәйкес келетін сан k= = .

ξ=Аcos( ξ –ығысу. А толқын амплитудасы. К толқ сан. Х қаш. k=2π/λ=2π/υT=ω/υ

12.Толқындық теңдеу. Серпінді толқын энергиясы. Умов векторы.

Жазық толқын теңдеуін толқындық сан арқылы өрнектейік ξ=acos( Негізен к векторлық шама, толқынның таралу бағытын көрсетеді k=ki. kx=kr, мұндағы r- радиус векторы, олай болса , кез келген бағытта таралатын жазық толқынның теңдеуі ξ=acos( .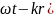

Изотропты және толқын энергиясын жұтпайтын ортада тарайтын толқын, дербес диференциалдық теңдеумен сипатталады, оны толқындық теңдеу деп атайды. Оның түрі: мұндағы . Лаплас операторы. Жазық толқынның осы теңдеуі қанағаттандыратын дәлелдеік. acos( , (7)

acos(

acos(

acos( ,

., ξ=- олай болса , ,

Лаплас операторы арқылы жазсақ дәлелдеу керегі де осы еді. Толқынның энергиясы.

Серпімді ортада тарайтын толқын энергиясы тербеліс жасайтын бөлшектердің кинетикалық энергиясы мен деформация салдарынан туатын потенциялдық энергияның қосындыларынан тұрады. Жазық қума толқын таралатын элементар көлем бөліп алайық Е_к және Е_р энергиялары мұндағы , жылдамдығы.

Толқын энергиясы

Энергияның тығыздығы w =

Жазық толқын үшін

Онда w= орташа мәні . Тараған толқын көзімен бірге энергия тығыздығы да тасымалданады. Кеңістіктің әр түрлі нүктелеріндегі энергия ағынын сипаттау үшін энергия ағынының тығыздығы деп аталатын векторлық шама еңгізу, оны алғашқы рет Н. Умов енгізгін j= . Мұндағы Ф энергия ағыны Ф= .

Умов векторының абсолюттік шамасы толқынның интенсивтілігін береді. I=│ │, I=│ │= . Амплитудасы A= интенсивтілігі I= . Жұтылатын ортадағы жазық толқынның теңдеуі .