МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Кафедра: «Путь и строительство железных дорог»
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
по дисциплине:
«Расчет и проектирование элементов железнодорожного пути »
Выполнил: студент 4 курса
гр.291
Ахметов В.В. Проверил:
Ершов В.В.
Самара2012
Изменение длины рельсов при колебаниях температуры.
1.1.В рельсосварочном предприятии изготовлена рельсовая плеть длиной
L п = 610, м при температуре tº= +5,С.Какую длину плети следует указать на внутренней стороне шейки рельса. Какая ещё информация располагается там же?
Изменение длины рельсовой плети составит
∆L=0.0000118L(20-t),
∆L=0,0000118∙740∙(20-5)= 0,164 м.
На внутренней стороне шейки рельса должна быть указана длина
610+0,164=610,164 м.
Допустим, что номер плети по проекту 12, плеть правая. Она уложена в путь 12 июня 2004 г. при температуре закрепления tо=+30ºС. Тогда маркировка такой плети имеет вид:
42-317-740,08-12п-12.06.04 +5
1.2.Какая продольная температурная сила возникает в рельсах Р65 при нулевых зазорах и повышении температуры на ∆t=30ºС?
Площадь поперечного сечения рельса Р65 равна F=82,7 см². Сжимающая рельс продольная температурная сила будет равна
Pt=σtF=αEF∆tр,
где F- площадь поперечного сечения рельса,см²;
αE=250 Н/см²∙град.
Рt =250∙82,7∙30=620250 Н. Таким образом, в рельсе типа Р65 при невозможности изменения его длины ( нулевые стыковые зазоры ) и повышении его температуры относительно нейтральной на 20ºС возникает сжимающая продольная температурная сила более 62т.
1.3. Определить длину L 1рельсовой плети, размещённой на роликовых опорах, при изменении её температуры на ∆t=35 ºС. До изменения температуры плеть имела длину L=740 м.
Изменение длины рельса ∆L, как свободного стержня, при изменении его температуры может быть определено по формуле
∆L=αL∆tр,
где α- коэффициент линейного расширения рельсовой стали;
α=0,00001181/град;
∆tр- изменение температуры рельса,ºС,
L- длина рельса, м.
∆L=0,0000118∙610,164∙30=0,22м.
Таким образом, при изменении температуры свободно лежащего рельса длиной 610 м на 30ºС его длина увеличилась на 220 мм. В этом случае ничто не препятствовало этому изменению и напряженное состояние рельса ни возникло.
1.4. На сколько должна изменится температура рельса Р65, чтобы стыковое сопротивление R = 100000 Н было преодолено?
Величину изменения температуры рельса ∆tн, при которой это произойдёт, можно определить по следующей формуле ∆tн = R/αEF,
где R- величина стыкового скрепления, кг
∆tн = 100000/(250∙82,7)≈5ºС.
1.5.
Рельсовая плеть длинной L=610 закреплена при tо=50С. Уравнительный пролёт состоит из трёх пар уравнительных рельсов длиной 12,5 м. Величины
стыковых зазоров в уравнительном пролете равны δ=10мм. Определить, произойдёт ли в заданном географическом районе (ст. Арзамас ) смыкание зазоров при tmax max ? Будет ли достигнут конструктивный максимум зазоров (2,1 см) в уравнительном пролете при tmin min?
Примем для решения остальные необходимые параметры (кроме известных по п.п. 1-4):
tmax max=57ºС, t min min= - 45 ºС,
стыковое сопротивление R=100000 Н,
погонное сопротивление продольному смещению рельсовой плети р = 80 Н/см.
Смыкание зазоров в уравнительном пролете возможно только при повышении температуры. Диапазон температур (∆t+), при которых конец рельсовой плети смещается в сторону уравнительного пролета (с учетом сопротивления стыкового скрепления ∆tн = 5 ºС) для заданных tз = 25ºС и t max max =55ºС равен
∆t = tmax max – tз - ∆tн = 57 –25– 5 =27 ºС
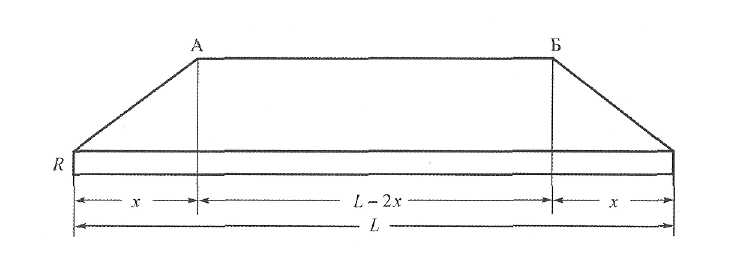
Определим длину х участка продольной деформации рельса при повышении его температуры до значения tmax max=57ºС относительно tз = 25ºС
Длина активного концевого участка x может быть найдена из выражения
x=αEF∆t+ / p
x =250 Н/см.град·82,7 см² ·270С/80 Н/см=6977,8см
Смещение конца рельса при такой температуре после преодоления стыкового сопротивления равно
∆L+=0,5αx ∆t+ .
∆L+ =0,5·0,0000118·6977,8см·27 = 1,11 см.
При повышении температуры для полного смыкания всех 4-х зазоров в уравнительном пролете конец рельсовой плети должен переместиться в сторону уравнительных рельсов на ∆L1+ = δ Ф * 4 = 7 *4 = 28 мм
Так как∆L+ < ∆L1 +,то есть 27 мм < 28 мм, то смыкания зазоров в уравнительном пролете не произойдет.
Повторим расчеты для случая понижения температуры.
Раскрытие (увеличение) зазоров в уравнительном пролете возможно только при понижении температуры. Диапазон температур (∆t_-), при которых зазоры увеличиваются за счет смещения конца рельсовой плети в сторону её середины (с учетом сопротивления стыкового скрепления ∆tн = 5 ºС) для заданных tз = 25ºС и t min min = - 45ºС равен
∆t_- = tз - ∆tн - t min min = 25 – 5 – (- 45) = 65 ºС
Определим длину х участка продольной деформации рельса при понижении его температуры до значения t min min = - 45ºС
x = αEF∆t- / p =250∙82,7∙65/80=16798 см
Смещение конца рельса при понижении температуры после преодоления стыкового сопротивления равно
∆L=0,5αx ∆ t - .
∆L - =0,5·0,0000118·16798·65 = 6.44см.
При понижении температуры до t min min= - 45 ºС для полного (конструктивного) раскрытия всех 4-х зазоров в уравнительном полете до δ max = 2,1 см состояние зазоров позволят переместиться концу рельсовой плети в сторону середины плети на величину∆L1 -, значение которой определяется формулой
∆L1 - = (δ max - δ Ф) * 4 = (2,1 – 1,0)*4 = 4,4 см
Так как при интервале температур ∆t_- возможное перемещение конца плети ∆L - = 6.44 см , а для полного раскрытия зазоров достаточно ∆L1 - = 4,4 см, то есть ∆L- > ∆L1 - то в уравнительном пролете произойдет полное их раскрытие.