11. Пучок прямых, уравнение пучка прямых.

Множество всех прямых плоскости, проходящих через данную точку , будем называть пучком прямых, проходящих через точку .

Рассмотрим множество всевозможных прямых, проходящих через некоторую точку и не параллельных оси . Пусть – уравнение произвольной прямой из указанного множества. Тогда . Подставляя найденное выражение для коэффициента в уравнение прямой, получим

Уравнение любой прямой, проходящей через точку и не параллельной оси , получается из уравнения (42) при соответствующем подборе углового коэффициента . Это уравнение называется уравнением пучка прямых, проходящих через точку

Пусть прямые заданные общими уравнениями

пересекаются в единственной точке .

Справедлива следующая теорема:

Теорема 2.2. Для того, чтобы прямая ,заданная общим уравнением принадлежала пучку прямых, проходящих через точку , необходимо и достаточно, чтобы существовали такие действительные числа и β, , что , , .

Доказательство. Докажем сначала достаточность.

Пусть выполнены равенства (45) Докажем, что прямая принадлежит пучку . Для этого достаточно доказать справедливость равенства

Так как, точка принадлежит как прямой , так и прямой , то её координаты , удовлетворяют равенствам

. (46)

Рассмотрим выражение . Подставляя в место коэффициентов соответствующие выражения из равенств (45), получим

Достаточность доказана.

Докажем необходимость. Пусть прямая задана её общим уравнением принадлежит пучку , т.е. проходящих через точку .

Покажем, что существуют такие действительные числа и β, , что верны равенства (45).

Пусть произвольная, отличная от , точка прямой . Положим . Поскольку точка не может одновременно лежать на , то по крайней мере одно из чисел или отлично от нуля.

Рассмотрим прямую заданную уравнением (47)

Из равенств

.

Следует, что точки и лежат на прямой, заданной уравнением (47).

Так как, через две различные точки и проходит единственная прямая, то прямая совпадает с прямой, заданной уравнением (47). Необходимость доказана.

Из теоремы следует, что прямая с общим уравнением принадлежит пучку прямых, проходящих через точку пересечения двух прямых

Тогда и только тогда, когда уравнение прямой можно представить в виде

Заметим, что уравнение любой прямой, проходящей через точку пересечения прямых можно получить путём соответствующего подбора и β.

В частности, если , , мы получим уравнение прямой . Если , мы получим уравнение прямой .

12. Нормированное уравнение прямой. Расстояние от точки до прямой.

Нормированным уравнением прямой называется уравнение вида , которое получается из общего уравнения путём деления его на длину нормального вектора .

Расстояние от точки до прямой.

Докажем, что расстояние точки до прямой, заданной общим уравнением равно

Д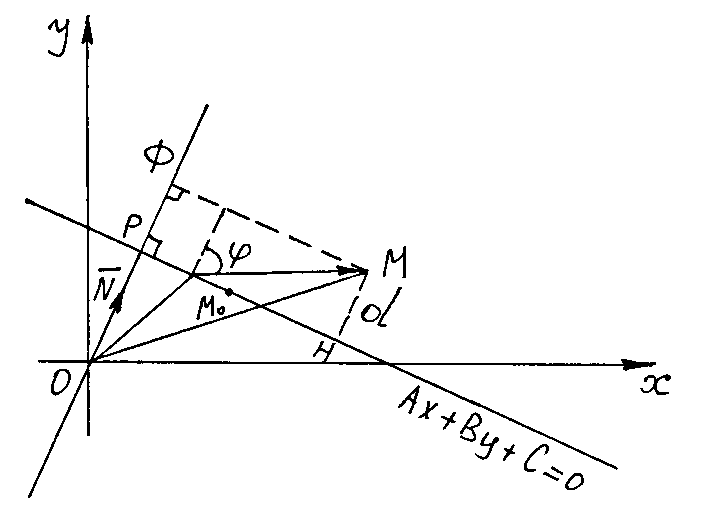 оказательство. Рассмотрим на плоскости произвольную прямую , определяемую общим уравнением и вектор .

Единичный вектор коллинеарен вектору , а поэтому ортогонален к прямой . Приложим вектор к началу координат. Пусть - точка пересечения прямой, на которой лежит вектор и прямой . Возьмём на плоскости произвольную точку , а на прямой -произвольную точку . Пусть – проекция точки на прямую, на которой лежит вектор . Тогда очевидно, что и будет расстоянием от точки до прямой . Пусть - угол между векторами и тогда

Справедливость формулы (49) доказана.

13. Эллипс.Эллипсом называется множество всех точек плоскости, для которых сумма расстояний от двух данных точек плоскости, называемых фокусами, есть величина постоянная, большая чем расстояние между фокусами.

Обозначим фокусы эллипса через и , расстояние между фокусами через , сумму расстояний от произвольной точки эллипса до фокусов через . Тогда по определению , т.е. .

Введём прямоугольную систему координат так, чтобы фокусы эллипса лежали на оси абсцисс, а начало координат находилось в середине отрезка . Тогда фокусы имеют координаты , .

П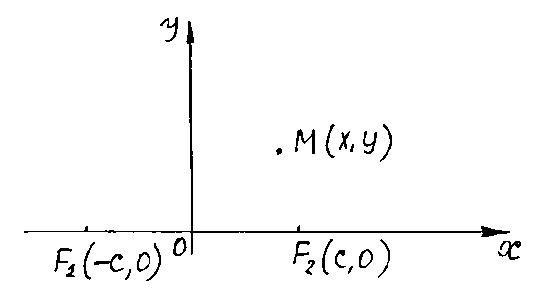 усть – произвольная точка плоскости, и - расстояния от точки до фокусов и соответственно. Числа и называются фокальными радиусами точки . Очевидно, что точка будет лежать на данном эллипсе тогда и только тогда, когда .

Найдём расстояния и .

Подставляя эти выражения в равенство (1), получим

Перенесём второй радикал в правую часть уравнения, а затем возведём обе части в квадрат

Возведём снова в квадрат обе части уравнения (4)

Обозначим через , тогда из уравнения (5) получим

Разделив обе части на , получим

Уравнение (7) получено из уравнения (3), поэтому координаты любой точки, удовлетворяющие уравнению (3) , будут удовлетворять и уравнению (7). Однако при упрощении уравнения (3) обе его части дважды возводили в квадрат, следовательно, могли появиться такие точки, координаты которых удовлетворяют уравнению (7), но не удовлетворяют уравнению (3).

Убедимся в том, что если координаты некоторой точки удовлетворяют уравнению (7), то они удовлетворяют и уравнению (3), что будет означать равносильность уравнений (3) и (7) .

Пусть – произвольная точка плоскости, координаты которой удовлетворяют уравнению (7).

Рассмотрим фокальный радиус точки -

Из уравнения (7) имеем.

Непосредственно из определения эллипса следует неравенство (10)

Из неравенств (9) и (10) следует, что

поэтому

Аналогично доказывается, что

Складывая и , получим . Т.е. получаем равенство (1). Из равенства (1) в свою очередь следует справедливость равенства (3). Таким образом, любая точка, координаты которой удовлетворяют уравнению (7), принадлежит эллипсу.

Уравнение (7) называется каноническим уравнением эллипса.

Заметим, что уравнение (7) содержит только члены с чётными степенями и , поэтому эллипс симметричен относительно осей и , а также относительно начала координат. Таким образом, можно знать форму эллипса, если установить вид той его части, которая находится в первом координатном угле.

Из уравнения (7) имеем .

Так как в первом координатном угле , то из равенства (11) имеем

И з последнего равенства вытекает:

1. Если , то , т.е. точка лежит на эллипсе.

2. При возрастании от 0 до уменьшается.

3. Если , то , т.е. точка лежит на эллипсе.

и в уравнении эллипса называются большой и малой полуосями.

Точки, в которых эллипс пересекает оси, называются его вершинами.

Заметим, что если , то уравнение (7) принимает вид . Это уравнение окружности радиуса с центром в точке . Т.е. окружность – частный случай эллипса.

Эксцентриситетом эллипса называется отношение , где - половина расстояния между фокусами, - большая полуось эллипса.

Эксцентриситет обычно обозначают буквой . Т.к. , то .

Принимая во внимание, что , найдём , откуда .

Из последнего равенство легко получается геометрическая иллюстрация эксцентриситета эллипса. При малых значениях 𝜀 числа и почти равны, т.е. эллипс близок к окружности. Если же 𝜀 близко к единице, то число весьма мало по сравнению с числом , т.е. эллипс сильно вытянут вдоль большой оси. Таким образом, эксцентриситет эллипса характеризует меру вытянутости.

Известно, что планеты и некоторые кометы движутся по эллиптическим траекториям. Оказывается, планеты движутся почти по окружностям, т.е. эксцентриситеты их орбит близки к нулю, а для орбит комет наоборот, эксцентриситет близок к единице. При этом в одном из фокусов находится солнце. Т.е. некоторые кометы то «сильно» приближаются к солнцу, то сильно удаляются от него.

14. Гипербола. Гиперболой называется множество всех точек плоскости, для которых модулю разности расстояний от двух данных точек плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Пусть и - фокусы гиперболы. Обозначим расстояние между фокусами и через , а модуль разности расстояний от произвольной точки гиперболы до фокусов через . По определению , т.е. . Введём на плоскости прямоугольную систему координат так, чтобы фокусы гиперболы лежали на оси абсцисс. А начало координат делило отрезок пополам. Тогда фокусы гиперболы имеют координаты . Выведем уравнение гиперболы в выбранной системе координат. Пусть – произвольная точка плоскости. Обозначим расстояния от точки до фокусов и через и соответственно, т.е. , . Из определения гиперболы следует, что точка будет лежать на данной гиперболе тогда и только тогда, когда . Т.е. .

Подставляя выражения

в равенство (12), получим

Очевидно, что точка лежит на гиперболе тогда и только тогда, когда её координаты удовлетворяют уравнению (14). Перенесём второй радикал в правую часть уравнения, после чего возведём обе части в квадрат.

Снова возведём обе части уравнения в квадрат:

Обозначим получим или

Как и для случая эллипса, можно доказать, что при возведении в квадрат не получены «лишние» точки, т.е. координаты точек гиперболы и только они удовлетворяют уравнению (17). Уравнение (17) называется каноническим уравнением гиперболы.

Исследуем форму гиперболы по её каноническому уравнению.

Уравнение (17) содержит только чётные степени координат и . Следовательно гипербола симметрична относительно осей и , а также относительно начала координат. Поэтому достаточно рассмотреть ту часть гиперболы, которая лежит в первом координатном угле. Для этой части гиперболы , поэтому, разрешая уравнение (16) относительно , а затем извлекая квадратный корень, получи

Из равенства (18) вытекают следующие утверждения.

1. .

2. Если , то , т.е. точка принадлежит гиперболе.

3. Если , то , причём возрастает неограниченно при неограниченном возрастании . Точка на гиперболе движется с ростом «вправо» и «вверх», её начальное положение – точка .

В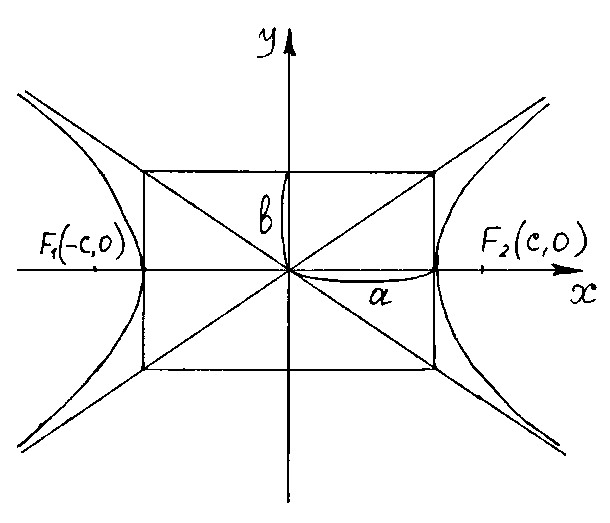 ид гиперболы теперь можно легко установить, используя симметрию относительно координатных осей.

Рассмотрим прямую, заданную её уравнением с угловым коэффициентом

Прямая, заданная уравнением (19) называется асимптотой гиперболы. Покажем, что точка уходя по гиперболе в бесконечность, неограниченно приближается к прямой, определяемой уравнением (19).

Возьмём произвольное значение и рассмотрим две точки и , где

и . Тогда точка лежит на гиперболе, а точка - на прямой (19). Очевидно, прямая перпендикулярная оси . Найдём длину отрезка .

П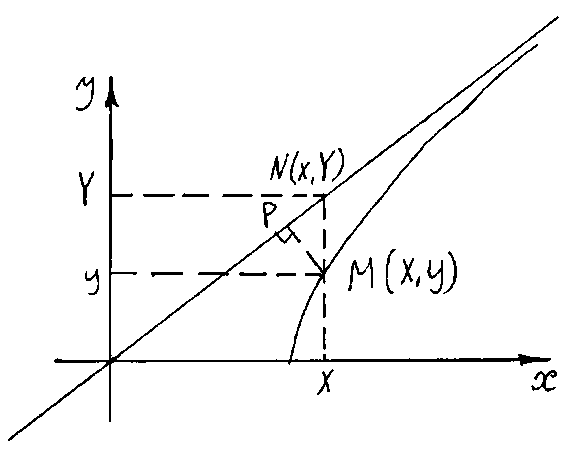 режде всего заметим, что , т.е. . Это означает, что точка лежит под точкой . Таким образом

Из последнего равенства следует, что при неограниченном увеличении длина отрезка уменьшается и приближается к нулю, т.к. знаменатель неограниченно увеличивается, а числитель есть постоянная величина . Обозначим через основание перпендикуляра, опущенного из точки на прямую (19). Тогда - расстояние от точки до этой прямой. Очевидно, , а т.к. , то и подавно , т.е. точка неограниченно приближается к прямой (19).

Гипербола состоит из двух ветвей правой и левой и имеет две асимптоты: и .

Оси симметрии называются осями гиперболы, а центр симметрии (точка пересечения осей) – центром гиперболы. Одна из осей пересекается с гиперболой в двух точках, которые называются её вершинами. Эта ось называется действительной осью гиперболы. Другая ось не имеет общих точек с гиперболой и называется мнимой осью гиперболы. Прямоугольник со сторонами и называется основным прямоугольником гиперболы. Величины и называются соответственно действительной и мнимой полуосями гиперболы.

Рассмотрим уравнение , которое также определяет гиперболу; вершины её лежат на оси . Эта гипербола называется сопряжённой по отношению к гиперболе (17). Обе эти гиперболы имеют одни и те же асимптоты.

Гипербола с равными полуосями, т.е. называется равнобочной и её каноническое уравнение имеет вид .

Так как основной прямоугольник равносторонней гиперболы является квадратом, то асимптоты равнобочной гиперболы перпендикулярны друг другу.

Эксцентриситетом гиперболы называется отношение , где - половина расстояния между фокусами, - действительная полуось гиперболы. Эксцентриситет гиперболы обозначается буквой 𝜀. Так как , то . Учитывая, что , найдём

откуда .

Из последнего равенства легко получается геометрическое истолкование эксцентриситета гиперболы: чем ближе эксцентриситет к единице, тем меньше отношение , а это означает, что основной прямоугольник более вытянут в направлении действительной оси. Таким образом, эксцентриситет гиперболы характеризует форму её основного прямоугольник, а значит, и форму самой гиперболы.