8. Расстояние между двумя точками

Рассмотрим в пространстве декартову прямоугольную систему координат и точки и .

Очевидно, что – расстояние между двумя точками равно длине вектора . Следовательно

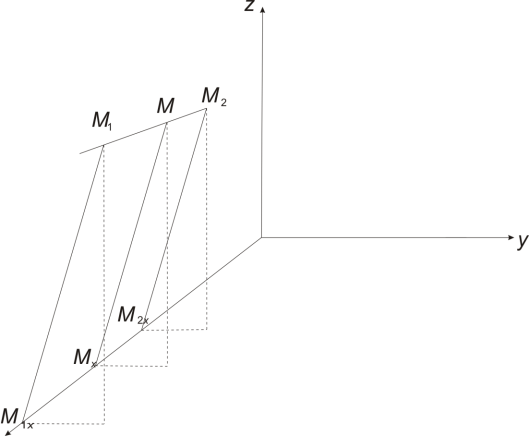
2. Деление отрезка в данном отношении.

Рассмотрим в пространстве две различные точки и прямую, проходящую через эти точки. Выберем на этой прямой некоторое направление. Тогда на полученной оси точки определяют направленный отрезок

Пусть - любая отличная от точка указанной оси. Число , где и - величины направленных отрезков соответственно, называется отношением, в котором точка делит направленный отрезок .

Замечание 1. При изменении направления на прямой, проходящей через точки , меняют знаки величины всех направленных отрезков. Поэтому отношение не зависит от выбора направления на прямой .

Введём в пространстве декартову прямоугольную систему координат , и пусть в этой системе координат точки имеют соответственно координаты , и . Пусть точка делит направленный отрезок в отношении , при этом будем считать, что .

В ыясним, как можно выразить координаты точки с помощью координат . Пусть , и - основания перпендикуляров, опущенных из точек и на ось . Очевидно, что точка делит направленный отрезок в отношении 𝜆, поэтому

, . Тогда из равенств (3) и равенства (2) найдём . Аналогично, проектируя точки на оси и повторяя проведённые выше рассуждения получим следующие формулы нахождения координат точки :

Формулы (4) называются формулами деления отрезка в данном отношении 𝜆.

Замечание 2. Очевидно, если , то точка делит отрезок пополам. В этом случае из формул (4) мы получим . (5)

Формулы (5) называются формулами деления отрезка пополам.

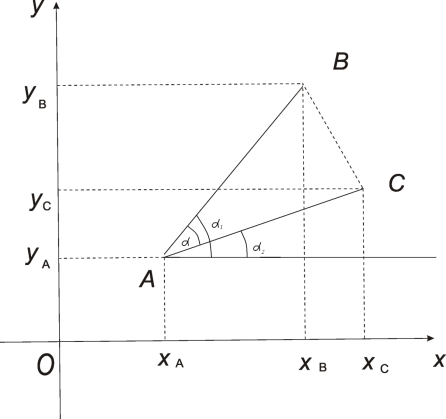
3. Формула площади треугольника на плоскости. Рассмотрим в плоскости прямоугольную систему координат . Пусть вершины треугольника имеют координаты , , .

Пусть и пусть и - углы наклона векторов и к оси .

В зависимости от расположения точек возможны следующие три случая:

1. ; 2. ; 3. .

Рассмотрим случай 1. Площадь треугольника можно найти по формуле

.

Учитывая, что

, получим

Аналогично устанавливается справедливость формулы (6) в случаях 2 и 3.

Замечание. Аналогичная формула верна и для случая n -угольника .

.

4. Полярная система координат.

Во многих задачах математики, наряду с прямоугольными координатами рассматриваются также полярные координаты. Полярные координаты вводятся следующим образом:

Рассмотрим на плоскости некоторую точку и выходящий из нее луч . Кроме этого укажем единицу масштаба. Точку будем называть полюсом.

Полярными координатами точки называются два числа , первое из которых (полярный радиус) равно расстоянию от полюса до точки , а второе (полярный угол) 𝜑 – углу, на который нужно повернуть против часовой стрелки луч до совмещения с лучом . При этом предполагается, что точка отлична от полюса. Для полюса полярный радиус равен нулю, а полярный угол не определен.

Тот факт, что точка имеет полярные координаты обозначается символом .

Для того, чтобы соответствие между отличными от полюса точками плоскости и парами полярных координат ) было взаимно однозначным, считают, что

Пусть точка имеет декартовы координаты и полярные координаты ρ, 𝜑.

Тогда прямоугольные координаты и полярные координаты ρ, 𝜑, очевидно связаны соотношениями: , при этом .