Билет 17.
1.Знайти розв’язок прямої задачі лінійного програмування шляхом графічного розв’язування двоїстої задачі й застосування теорем двоїстості:
Розв'язання.За відповідними правилами побудуємо двоїсту задачу: mах F = y1 + 3y2;
Задачі несиметричні. Двоїста задача має дві змінні, а отже, її можна розв’язати графічно.
Найбільшого значення цільова функція двоїстої задачі F досягає в точці В багатокутника ABCD. Її координати визначимо розв’язанням системи рівнянь:
→
Отже, Y* = (1,6; 1,6); mах F = 1,6+ 3*1,6 = 6,4.
Оптимальний план прямої задачі визначимо за допомогою співвідношень другої теореми двоїстості.
Підставимо Y* у систему обмежень двоїстої задачі і з’ясуємо, як виконуються обмеження цієї задачі:
→
Оскільки останнє обмеження для оптимального плану двоїстої задачі виконується як строга нерівність, то висновуємо, що третя змінна прямої задачі дорівнюватиме нулю х3 = 0 (перша частина другої теореми двоїстості).
Тепер проаналізуємо оптимальний план двоїстої задачі. Оскільки перші компоненти плану у1 = 1 та у2 = 0 додатні, то обидва обмеження прямої задачі для Х* виконуватиметься як строгі рівняння (друга частина другої теореми двоїстості).
Об’єднуючи здобуту інформацію, можна записати систему обмежень прямої задачі як систему двох рівнянь, в якій х3 = 0, та визначити решту змінних:
тобто Х* = (0,667; 0,7333; 0),
min Z = 8 0,667+ 8*0,7333 + 1 0 = 6,4.
Умова min Z = max F = 6,4 виконується, і тому
Х* = (0,667; 0,7333; 0); Y* = (1,6;1,6)
є оптимальними планами відповідно прямої та двоїстої задач.
Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму наступної задачі нелінійного програмування, визначити характер екстремуму:
,
Вводимо в цільову функцію множник лагранжа:
Z(x1,x2,λ1, λ2)= x2- x1-2x12 + λ1(12-3x1-4x2) + λ2(6+x1-2x2)
Знаходимо похідні:
По х1: -1-4х1-3 λ1+ λ2
х2: 1-4λ1-2 λ2
λ1:12-3x1-4x2
λ2: 6+x1-2x2
Прирівнюємо похідні виражені через лямбда
Звідси: х1=0; х2=3; λ1=-0.1; λ2=0.7
Формуємо матрицю Гессе:
0 0 3 4
= 0 0 -1 2
3 -1 -4 0
4 2 0 0
Визначаємо мінори 3-го та 4-го порядку:
=0; =100
Маємо знакосталий ряд, що визначає нашу функцію на мінімум.
Значення ЦФ=3.
Билет 18.
Знайти розв’язок прямої задачі лінійного програмування шляхом графічного розв’язування двоїстої задачі й застосування теорем двоїстості:
Розв'язання.За відповідними правилами побудуємо двоїсту задачу: mіп F = 2y1 + 0y2;
Задачі несиметричні. Двоїста задача має дві змінні, а отже, її можна розв’язати графічно.
Найменшого значення цільова функція двоїстої задачі F досягає в точці В багатокутника ABCD. Її координати визначимо розв’язанням системи рівнянь:
→
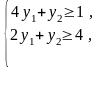
Отже, Y* = (-1,5; 7); mіп F = 2*(-1,5)+ 0*7 = -3.
Оптимальний план прямої задачі визначимо за допомогою співвідношень другої теореми двоїстості.
Підставимо Y* у систему обмежень двоїстої задачі і з’ясуємо, як виконуються обмеження цієї задачі:
→
2.Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму наступної задачі нелінійного програмування, визначити характер екстремуму:
,
.
Вводимо в цільову функцію множник лагранжа:
Z(x1,x2,λ1, λ2)= 8x1+2x12+4x1х2+x22+ λ1(6-6x1-2x2) + λ2(16-x1-8x2)
Знаходимо похідні: По х1: 8+4х1+4х2-6 λ1- λ2;
х2: 2х2+4х1-2 λ1-8 λ2; λ1: 6-6x1-2x; λ2: 16-x1-8x2
Прирівнюємо похідні виражені через лямбда
Звідси: х1=0.34; х2=1.96; λ1=-2.2112; λ2=1.213
Формуємо матрицю Гессе:
0 0 6 2
= 0 0 1 8
6 1 4 4
2 8 4 2
Визначаємо мінори 3-го та 4-го порядку:
=0
=2116 Маємо знакосталий ряд, що визначає нашу функцію на мінімум. Значення ЦФ=9.57
БИЛЕТ №19
Знайти розв’язок прямої задачі лінійного програмування шляхом графічного розв’язування двоїстої задачі й застосування теорем двоїстості:
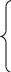
Спочатку побудуємо двоїсту задачу: F= y2+3y2 (Max)
y
1+
2y2
≤14
-5y1+3y2 ≤15
-4y1 -6y2 ≤ -24
Відповідно до обмежень будуємо прямі. Далі визначаємо корд. Напрямного вектора (1;3) потім знаходимо точки min(6;0) та max(0.923;6.54).
Будуємо ЦФ:
F(max)= 0.923 +3 * 6.54 =20.5
F(min) = 6
Розв’язки двоїстої задачі відповідають розвязкам прямої
БИЛЕТ № 20
4) Знайти розв’язок прямої задачі лінійного програмування шляхом графічного розв’язування двоїстої задачі й застосування теорем двоїстості:
Побудує двоїсту задачу
F(min) = 4y1-y2
Y
1+
y2
≥
1
Y1-y2 ≥ 8
Y1 -2y2 ≥ 10
Точка А(10;0) точка мінімуму
F(min)=40
5)
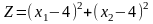за
умов:
х1
+х2≤6
.
Розв’язування.
У даному прикладі множина допустимих
розв’язків складається з двох окремих
частин, необмежених зверху . Цільова
функція аналогічно попередньому випадку
є колом з центром у точці М (4; 4).
Функція Z має два локальних мінімуми: в
точці А (
),
і в точці В (
).
Значення функціонала в цих точках однакове і дорівнює:
.
Отже, маємо два альтернативні оптимальні плани.
Билет № 21
Визначити (застосовуючи теореми двоїстості й не розв’язуючи задачі симплексним методом), чи оптимальні запропоновані плани задачі лінійного програмування:
а) x=(10;10/3);
б) x=(20;10);
в) x=(10/3;10/3).
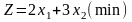
Формуємо двоїсту задачу згідно правил побудови двоїстих задач
Min F = -30y1+10y2
-2y1+y2+y3
≤2
-3y1+ y2 – y3 ≤3
А) Х = (10;10/3)
Підставляємо значення нашої точки в наші обмеження для визначення того чи задовольняються вони.
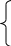30=30
16.6>10
6.7 > 0
План допустимий і для нього F = 30. Визначимо оптимальний план двоїстої задачі користуючись другою теоремою двоїстості. Оскільки Х1>0, та X2>0 то згідно з другою теоремою двоїстості можна записати перше та друге обмеження рівнянням.
-2y1+y2+y3
≤2
y1=-1
-3y1+ y2 – y3 ≤3 y2=0
Y3=0
Б) Х = (20;10)
Підставляємо значення нашої точки в наші обмеження для визначення того чи задовольняються вони.
7 0≠30
40>10
10≥0
Так як обмеження не виконується дана точка не може бути оптимальним розв’язком нашої задачі.
В) (10/3;10/3)
Підставляємо значення нашої точки в наші обмеження для визначення того чи задовольняються вони.
1
6.6<30
10=10
0=0
F=16.6
5) Знайти мінімальне значення функції:
за умов:
.Розв’язування.
У даному прикладі множина допустимих
розв’язків складається з двох окремих
частин, необмежених зверху (рис. 8.2).
Цільова функція аналогічно попередньому
випадку є колом з центром у точці
М (4; 4). Функція Z має два локальних
мінімуми: в точці А (
),
і в точці В (
).
Значення функціонала в цих точках однакове і дорівнює:
.
Отже, маємо два альтернативні оптимальні плани.