[Править]Функции состояния

Функции состояния зависят только от текущего состояния системы и не зависят от пути, по которому система пришла в это состояние.

Функции состояния в термодинамике включают:

• температуру,

• давление,

• объём,

• энтропию,

а также термодинамические потенциалы.

В зависимости от выбранной модели некоторые из этих величин, строго говоря, могут быть не функциями, а независимыми переменными.

Эти величины не являются независимыми. Связь между термодинамическими параметрами для конкретной системы называется уравнением состояния.

В случае, если известно каноническое уравнение состояния, задание любой пары параметров из следующих:

• энтропия и объём,

• энтропия и давление,

• температура и объём,

• температура и давление,

позволяет вычислить остальные два параметра.

[Править]Функции процесса

Функции процесса зависят не только от текущего состояния системы, но также и от пути, по которому система пришла в данное состояние.

Функции процесса в термодинамике включают:

• количество теплоты и

• термодинамическую работу.

Эти величины, однако, могут быть «превращены» в функции состояния с помощью интегрирующего множителя:

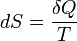• , где S (энтропия) — функция состояния.

• PdV = δA, где P (давление) и V (объём) — функции состояния.

Уравне́ние состоя́ния — уравнение, связывающее между собой термодинамические(макроскопические) параметры системы, такие, как температура, давление, объём, химический потенциал и др. Уравнение состояния можно написать всегда, когда можно применять термодинамическое описание явлений. При этом реальные уравнения состояний реальных веществ могут быть крайне сложными.

Термическое уравнение состояния

Термическое уравнение состояния связывает макроскопические параметры системы. Для системы с постоянным числом частиц его общий вид можно записать так:

Таким образом, задать термическое уравнение состояния значит конкретизировать вид функции 

[Править]Калорическое уравнение состояния

Калорическое уравнение состояния показывает, как внутренняя энергия выражается через давление, объем и температуру. Для системы с постоянным числом частиц оно выглядит так:

или, учитывая, что давление можно выразить из термического уравнения:

Каноническое уравнение состояния

Основная статья: Термодинамические потенциалы.

Каноническое уравнение представляет собой выражение для одного из термодинамических потенциалов (внутренней энергии,энтальпии, свободной энергии или потенциала Гиббса) через независимые переменные, относительно которых записывается его полный дифференциал.

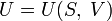•  (для внутренней энергии),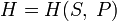

•  (для энтальпии),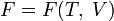

•  (для энергии Гельмгольца),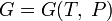

•  (для потенциала Гиббса).

Каноническое уравнение, независимо от того, в каком из этих четырех видов оно представлено, содержит полную информацию о термических и калорических свойствах термодинамической системы (предполагается, что известно и определение термодинамического потенциала, такое, как F = U − TS).

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнениеКлапейрона — Менделеева) — формула, устанавливающая зависимость между давлением,молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

где

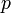•  — давление,

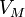•  — молярный объём,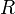

•  — универсальная газовая постоянная

•  — абсолютная температура,К.

Так как  , где   — количество вещества, а  , где   — масса,   — молярная масса, уравнение состояния можно записать:

Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

В случае постоянной массы газа уравнение можно записать в виде:

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

 — закон Бойля — Мариотта.

 — Закон Гей-Люссака.

 — закон Шарля (второй закон Гей-Люссака, 1808 г.)

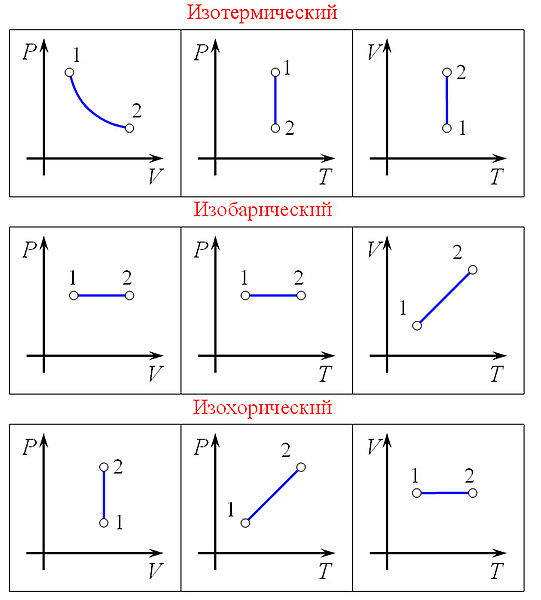
Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём или температура — остаются неизменными. Так, неизменному давлению соответствуетизобарный процесс, объёму — изохорный, температуре —изотермический, энтропии — изоэнтропийный (например, обратимыйадиабатический процесс). Линии, изображающие данные процессы на какой-либо термодинамической диаграмме, называютсяизобара, изохора, изотерма и адиабата соответственно. Изопроцессы являются частными случаями политропного процесса.

 Закон Гей-Люссака:

законом Шарля: 

законом Бойля — Мариотта:  PV = const.

Уравнение молекулярно-кинетической теории для давления идеального газа. Средняя энергия молекулы. Физический смысл температуры