Решения

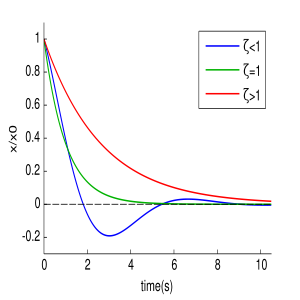
Зависимость графиков колебаний от значения ζ.

В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта.

• Апериодичность

Если  , то имеется два действительных корня, и решение дифференциального уравнения принимает вид:

В этом случае колебания с самого начала экспоненциально затухают.

• Граница апериодичности

Если  , два действительных корня совпадают  , и решением уравнения является:

В данном случае может иметь место вре́менный рост, но потом — экспоненциальное затухание.

• Слабое затухание

Если  , то решением характеристического уравнения являются два комплексно сопряжённых корня

Тогда решением исходного дифференциального уравнения является

Где   — собственная частота затухающих колебаний.

Константы c₁ и c₂ в каждом из случаев определяются из начальных условий: 

Волны в упругих средах. Продольные и поперечные волны

Среда называется УПРУГОЙ, или ЛИНЕЙНОЙ, если её деформация пропорциональна приложенной силе (аналогично закону Гука).

например: слабый удар молоточка по металлу. Деформации, возникающие в металле (смещения), будут пропорциональны приложенной силе (если, конечно, бить не очень сильно).

При достаточно малых деформациях практически все тела (в том числе жидкие и газообразные; в этом случае обычно говорят не "тело", а "среда") являются упругими.

УПРУГИМИ, или МЕХАНИЧЕСКИМИ волнами называются механические возмущения (деформации), распространяющиеся в упругих средах.

Тело, вызывающее эти возмущения при своём воздействии на среду, называется ИСТОЧНИКОМ волн.

Упругие волны часто называют ЗВУКОВЫМИ волнами, или просто ЗВУКОМ, так как человеческое ухо воспринимает большинство таких волн как звук (даже если и не воспринимает, все равно говорят о звуковых волнах).

Распространение упругих волн не связано с переносом вещества; частички среды колеблются около положения равновесия. (Когда вы слышите звук, вы не ощущаете ветер.)

Волны бывают продольные, поперечные и поверхностные.

Волна называется ПРОДОЛЬНОЙ, если частицы среды колеблются в направлении распространения волны. Например, обычный звук в воздухе.

Волна называется ПОПЕРЕЧНОЙ, если частицы среды (или тела) колеблются перпендикулярно распространению волны. Например, волны, бегущие по струнам.

ПОВЕРХНОСТНЫЕ волны наблюдаются на свободной поверхности жидкостей. Частицы жидкости при распространении такой волны колеблются как вдоль, так и поперёк направлению распространения волны.

Волны бывают бегущие и стоячие.

БЕГУЩИМИ называются волны, переносящие энергию в пространстве. При своём распространении такая волна вовлекает в колебания всё новые и новые частицы среды, которые при этом получают энергию от волны.

СТОЯЧИЕ волны образуются в результате суперпозиции двух одинаковых бегущих (друг другу навстречу) волн. Колеблющиеся частицы среды, разумеется, обладают энергией, но переноса энергии не происходит. Два одинаковых встречных потока энергии в сумме дают ноль.

В случае реальной среды наблюдается поглощение волн (так называется затухание волны в пространстве); механическая энергия колеблющихся частиц переходит во внутреннюю, тепловую энергию среды. Далее мы будем вести речь только о волнах, распространяющихся без поглощения, то есть в идеальных средах.

ЛУЧ - линия, касательная к которой в каждой точке совпадает с направлением распространения волны.

ГАРМОНИЧЕСКАЯ, или СИНУСОИДАЛЬНАЯ ВОЛНА - волна, при распространении которой частицы среды совершаютгармонические (синусоидальные) колебания.

Частота этих колебаний есть ЧАСТОТА ВОЛНЫ.

ВОЛНОВАЯ ПОВЕРХНОСТЬ или ВОЛНОВОЙ ФРОНТ - геометрическое место точек, в которых фаза колебаний частиц среды имеет одно и то же значение.

Волна называется ПЛОСКОЙ, если её волновые поверхности есть параллельные плоскости. Например, волны от плоского протяженного источника.

Волна называется СФЕРИЧЕСКОЙ, если её волновые поверхности есть концентрические сферы. Например, волны от точечного источника.

УРАВНЕНИЕМ ВОЛНЫ называется зависимость колеблющейся величины от координат и времени. Например, при колебаниях струны - это зависимость от координат и времени смещения какой-либо точки струны от положения равновесия; при колебаниях воздуха - зависимость давления воздуха от координат и времени.

Уравнение плоской волны. Длина волны. Волновое число.