41.Многоканальные Системы Массового Обслуживания(смо) с отказами

Рассмотрим n-канальную СМО с отказами. Будем нумеровать состояния системы по числу занятых каналов (или, что в данном случае то же, по числу заявок, находящихся в системе или связанных с системой). Состояния системы:

— все каналы свободны;

—занят ровно один канал, остальные свободны;

—заняты ровно к каналов, остальные свободны;

—заняты все n каналов.

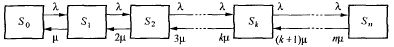
Рис. Многоканальной СМО с отказами

Около стрелок поставлены интенсивности соответствующих потоков событий. По стрелкам слева направо систему переводит один и тот же поток — поток заявок с интенсивностью 𝛌. Если система находится в состоянии (занято к каналов) и пришла новая заявка, то система переходит в состояние

Определим интенсивности потоков событий, переводящих систему по стрелкам справа налево. Пусть система находится в состоянии S1(занят один канал). Тогда, как только закончится обслуживание заявки, занимающей этот канал, система перейдет в S0; значит, поток событий, переводящий систему по стрелке S₁ – S₀ , имеет интенсивность μ. Очевидно, если обслуживанием занято два канала, а не один, поток обслуживания, переводящий систему по стрелке S₂ – S₁ будет вдвое интенсивнее (2μ); если занято k каналов — в к раз интенсивнее (kμ). Соответствующие интенсивности указаны у стрелок, ведущих справа налево.

Можно составить уравнения Колмогорова для вероятностей состояний:

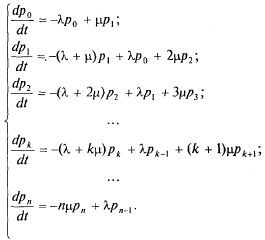
Уравнения называют уравнениями Эрланга. Поскольку при t = 0 система свободна, начальными условиями для их решения являются:

Имея вероятности состояний можно найти характеристики эффективности СМО: относительную пропускную способность q, абсолютную пропускную способность А и вероятность отказа .

Вероятность отказа. Заявка получает отказ, если приходит в момент, когда все и каналов заняты. Вероятность этого равна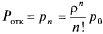

Относительная пропускная способность. Вероятность того, что заявка будет принята к обслуживанию (относительная пропускная способность а), дополняет до единицы:

Абсолютная пропускная способность:

42. Система массового обслуживания с ожиданием.

Если процесс ожидание ничем не ограничен, то это система с чистым ожиданием.

Если есть ограничение по длине очереди или по времени ожидание, то это система смешанного типа.

n, m S₀, S₁, S₂, …., S_k, S_n-1, S_n, S_n+1, S_n+2, …, S_n+m

P_0, P₁, P₂,….. P_k, ……………………………… P_n+m

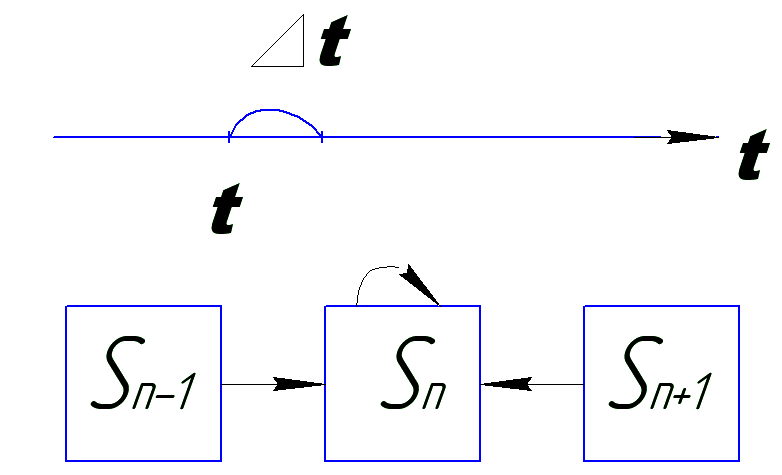
1)Система может происходить в сос-и S_n, если произойдет одно из 3 событий, событие А, зак. В том, что система находиться в состоянии S_n, и за интервал времени 𝜟t, не приняла заявка, и освоб. из постов.

2) Система состояний S_n-1, и за 𝜟t→ S_n; т.е пришла 1 заявка, и не освободился ни один из n постов.

3)Система в S_n+1, и за 𝜟t→ освобод. один из n постов и не пришла не одна заявка.

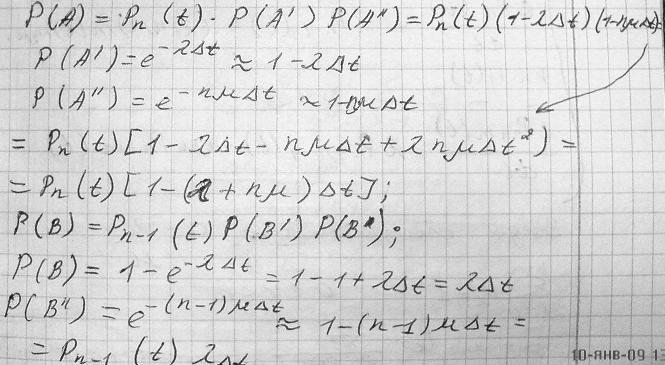
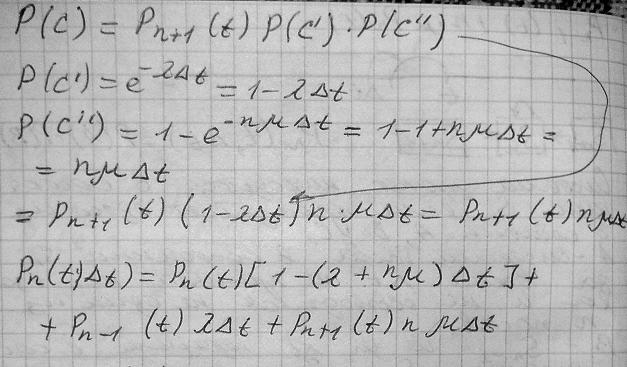
43. Детерминированная задача упорядочения

1. Детерминированная задача упорядочения Задача упорядочения – задача определения оптимальной последовательности обработки изделий ,определение наилучших маршрутов увеличения определения оптимальных алгоритмов обработки массивов информации.

1,2,t_1j,t_2j; T_общ.min-?

j	1	2	3	4	5	6
t1j	6	4	6	5	7	4
t2j	5	2	3	6	6	7

Считаем что время перехода с машины на машину незначительное или одинаковое, или оно учитывается в t1j,t2j.Поэтому время перехода в явном виде не учитывается.

T_общ.=

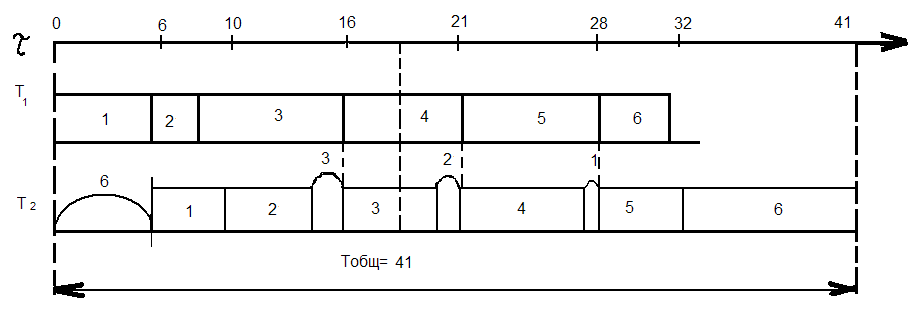
Алгоритм разработки оптимальной последовательности изделий включает ряд этапов:

-осуществление поиска min время обслуживания из всей таблицы

-перестановка элементов ,при этом если наименьшее время относится к 1 машине ,то эту деталь ставят на 1 место .Если наименьшее время относится ко 2 машине ,то деталь становится на последнее место. Если есть два наименьших времени в обоих строках , то деталь имеющая время на 1 машине переставляется вперед ,а относятся ко 2 машине на последнее место.

Если 2 наименьших элемента в 1 строке, то первой перемещается деталь, имеющая меньший 2 элемент.

Процедура повторяется, пока не будет составлять полный алгоритм обработки .

6,4,5,1,3,2. T_общ=34=29+5

Алгоритм Джонсана может быть распространен на 3 машинах если выполняются условия:

1.Если минимальное время обработки на 1 машине = максимальному времени на 2

2.Если минимальное время обработка на 3 машине ≥обработки на 2

Время обработки по каждому изделию складываются