
- •4. Классификация видов моделирования
- •11. Среднее значение и методы их выполнения
- •12. Вычисление среднего для интервального ряда
- •15. Оценка точности измерений
- •16. Формулировка метода наименьших квадратов
- •17. Отыскание параметров линейной ф-ии методом наименьших квадратов.
- •19. Приближённые и упрощённые методы отыскания параметров, входящих в формулы нелинейно
- •20. Отыскание параметров многочлена
- •21. Выбор оптимальной степени многочлена
- •22. Сглаживание эмпирических данных
- •25. Оценка параметров регрессионной модели
- •26. Оценка значимости коэффициентов регрессионной модели и проверка ее на адекватность
- •27.Определение области экстремума регрессионной модели.
- •28.Основные положения дробно-факторного планирования эксперимента.
- •31. Основные подходы к построению матмодели.
- •32. Основные типы моделей: непрерывно-детерминированные, дискретно-детерминированные, дискретно-стахостические, непрерывно-стахостические.
- •41.Многоканальные Системы Массового Обслуживания(смо) с отказами
- •42. Система массового обслуживания с ожиданием.
- •43. Детерминированная задача упорядочения
- •2.Задачи упорядочения работ на основе моделей мультипроцессорная системы
- •44.Детерминированная задача согласования
- •47. Априорное и итерационное ранжирование.
- •48. Принятие решений в условиях неопределенности.
31. Основные подходы к построению матмодели.
Исходная информация при моделировании:
- данные о назначении или условиях работы системы.
Уровень абстрогирования зависит от того какие вопросы мы хотим решить.
Матем. схема – звено при переходе от содержательного к формальному описанию процесса функционирования систем
описыв.
модель
модель
формал.
S1,S2,…,Sn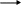

W
V Y
W(XW1,XW2)
V(XV1,XV2)
Y(XY1,XY2)
Процесс функционирования системы описыв. оператором F, который в общем виде преобр. входные воздействия в выходные характеристики.
Y=F(v,w,s,t) – з-н функционирования систем
Его задают в виде ф-й, логических условий, в табличной форме, словесных правил.
Алгоритм функционирования – метод получения выходных характеристик с учетом воздействий факторов внешней среды во времени.
T/Δt=N
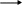
 Δt
0;N
∞,N‹‹∞
Δt
0;N
∞,N‹‹∞

0
T
Если подмножество внешних воздействий не содержит случайностей то модель дотерминированна, в противном случае - стохастическая (вероятностная).
Типовые алгоритмические схемы:
- непрерывно
детерминирован. модели: N
∞, V,W,S
– не случайные,
непрерывно
детерминирован. модели: N
∞, V,W,S
– не случайные,
-дискретно-детерминированные: N‹‹∞, V,W,S – не случайные,
-дискретно-вероятностные: N‹‹∞, V,W,S – случайные,
- непрерывно-вероятностные: N ∞, V,W,S –случайные.
32. Основные типы моделей: непрерывно-детерминированные, дискретно-детерминированные, дискретно-стахостические, непрерывно-стахостические.
Н епрерывно-детерминированные модели (N ∞, V,W,S – не случайные) моделируют непрерывный процесс для случайных моделей. Для этого используют диф. уравнения.
Дискретно-детерминированная модель (N‹‹∞, V,W,S – не случайные) хар-ся тем, что система изменяет свое внутр. состояния лишь в опр. момент времени
S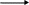

V Y Y
Y=F(v,s,t), V-входной алфавит,Y-выходной алфавит, S-алфавит возм. состояний
|
S0 |
S1 |
…. |
Sn |
V1 |
Z(V1,S0) |
Z(V1,S1) |
|
|
V2 |
Z(V2,S0) |
|
|
|
… |
|
|
|
|
Vm |
Z(Vm,S0) |
|
|
Z(Vm,Sn) |
Дискретно-стахостическая (вероятностная) модель. (N‹‹∞, V,W,S – случайные) такие матем. схемы предст. в виде вероятностного автомата.
Вероятностный автомат – потактный преобразователь информации, функционир. которого в каждом такте зависит от предыдущего состояния и вероятности возм. переходов в др. состояния при появлении входного сигнала.
S0,S1,…,Sn
Pi,y
Н епрерывно-стахостическая ( вероятностная) модель (N ∞, V,W,S –случайные)описывает непрерывные во времени случайные процессы, эти мат. схемы описывают функционирование систем массового обслуживания.
№ 33 Последовательность разработки модели.
При разработке и реализации модели определяются требования:
Модель должна обеспечивать необходимый набор сцепок с необходимой точностью и достоверностью;
Модель должна иметь гибкую структуру для возможности воспроизведения различных ситуаций;
Модель должна иметь блочную структуру;
Минимальную длительность разработки и реализации модели;
Модель должна иметь возможность реализовываться на ЭВМ.
Моделирование на ЭВМ применяется:
Для исследования систем до того как они спроектированы с целью определения характеристик;
Для анализа и синтеза возможных вариантов систем с целью выбора наилучшего варианта;
При эксплуатации систем для получения информации, дополняющая результаты лабораторных и эксплуатационных испытаний.
Существует 3 основных этапа моделирования систем:
Построение концептуальной модели системы и её формализация;
Алгоритмизация систем и ее машинная реализация;
Получение и интерпретация результатов моделирования.
№ 34 Построение концептуальной модели.
Разработка концептуальной модели состоит из этапов:
Постановка задачи моделирования:
- Выбор методики решения задачи;
- Определение масштаба задачи;
2. Анализ задачи моделирования:
- Выбор критерия оценки эффективности работы системы;
- Определяются зависимые и независимые переменные модели;
- Предварительно разрабатывается алгоритм моделирования;
3. Формирование требований и исходной информации и организации её сбора:
- Сбор информации о самой системе и внешней среде;
- Анализ имеющихся экспериментальных данных;
- Выбор методов и средств обработки информации.
4. Выдвижение гипотез и принятие предположений
5. Определение параметров и переменных моделей.
П ри
разработке модели определяется
подмножество воздействий Х, подмножество
внешних воздействий У, подмножество
параметров сист. S
и подмножество выходных параметров W.
ри
разработке модели определяется
подмножество воздействий Х, подмножество
внешних воздействий У, подмножество
параметров сист. S
и подмножество выходных параметров W.
Каждый параметр каждого подмножества необходимо описать, описание включает определение параметра и его характеристика, символ обозначения, единицы измерения и диапазон измерения.
Установление основного содержания модели:
- Формируется структура системы и алгоритм ее поведения;
7. Выбор критериев моделирования (эти критерии могут быть частные и интегральные);
8. Определение процедур аппроксимации результатов моделирования;
9. Описание концептуальной модели:
- Модель описывается в абстрактных терминах и понятиях;
- Осуществляется попытка описать поведение системы с использованием типовых математических схем;
- Окончательно принимаются гипотезы и предположения;
- Окончательно выбираются процедуры аппроксимации;
10. Проверка достоверности концептуальной модели на этом этапе достаточно сложно осуществлять оценку достоверности концептуальной модели.
№35.Алгоритмизация модели и ее машинная реализация
Алгоритмизация модели:
1) Построеение логической схемы модели.
Логическая схема – алгоритм перехода системы из состояния в состояние. Алгоритм представляется в виде совокупности основных и вспомогательных блоков, взаимосвязанными между собой. Основные осуществляют моделирование систем, а вспомогательные осуществляют разработку и фиксацию.

2)Получение математических соотношений.
Окончательно выбирают математич. аргумент для решения поставленной задачи.
3)Проверка достоверности логической схемы модели. Проаверяются:
1.возможность решения поставленной задачи.
2.точность отражения замысла логической схемы.
3.полнота логической схемы модели.
4.выбор вычислительных средств.
Для этого оценивают:
а)получение необходимых программных и технических средств.
б)доступность вычислительных средств.
в)возможность реализации модели на имеющихся ЭВМ.
г)сотавление плана работ по программированию:
- выбор языка моделирования.
- указание типа или модели ЭВМ.
- оценка требуемого объекта.
- оценка затрат машинного времени на моделирование.
- построение схемы программы.
5)Разбиение модели на блоки.
6)Разработка теории входных и выходных параметров системы.
7)Проведение программирования на основе алгоритма схемы программы.
8)Проверка достоверности программы. Для этого осуществляют прогон тестовых задач по отдельным блокам модели и проверяют работ модели на конкретном примере.
9)Составление документации по моделям.
Документация включает:
1.логическую схему модели
2.принятое обозначение в программе
3.текст программы
4.перечень входных и выходных величин.
5.инструкции пользователю для работы с программой.
6.оценка затрат машинного времени с указанием ресурсов по памяти.
№36.Основные определения теории массового обслуживания
Пропускная способность бывает:
- Абсолютная
- Относительная
Абсолютная – это среднее число заявок, которые может обслужить система в единицу времени.
Относительная – это отношение количества обслуженных заявок к количеству поступивших за какой-то промежуток времени.
Теория массового обслуживания(ТМО) устанавливает зависимость между характером потока заявок производительностью каналов, их числом и эффективностью обслуживания.
Характеристики эффективности системы массового обслуживания(СМО):
1)Пропускная способность
2)Среднее время простоя каналов и системы вцелом.
3)Среднее время ожидания в очереди
4)Среднее время обслуживания
5)Вероятность обслуживания
S-состояния; P- вероятности;
№37 Характеристика потоков событий
Поток событий – это последовательность событий, происходящих одно за другим, по не одновременно в какие-то моменты времени.
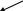
 ПОТОКИ
СОБЫТИЙ
ПОТОКИ
СОБЫТИЙ
Однородные Неоднородные
Однородные – это одинаковые события, различающиеся только моментами появлений(наступлений)
Неоднородный – поток неоднороден, если он хар-ся моментами появлений и набором других хар-тик.

Регулярные Случайные
- регулярные – если события следуют в строго определенный момент времени
- случайные – для них свойственны непредсказуемость моментов
Ординарные Неординарные
П
 оток
ординарный, если вероятность наступления
одновременно нескольких событий
принебрежительно мала.
τ
оток
ординарный, если вероятность наступления
одновременно нескольких событий
принебрежительно мала.
τ
 τ
τ
τ
P0(τ,
![]() )+P1(τ,
)+P>1(τ,
)=1
)+P1(τ,
)+P>1(τ,
)=1
Для
ординарного потока потока P0(τ,
)+P1(τ,
)![]() 1
1
Для неординарного потока событий возможно одновременное появление нескольких событий

Стационарные Нестационарные
Стационарным называется поток для которого вероятность появления того или иного числа событий, зависит только от длины участка и не зависит от его положения на оси времени.
Характеристикой стационарного потока является среднее число событий, происходящее за интервал времени .
N=0![]() P0(τ,
)+1
P1(τ,
)=
P1(τ,
)
P0(τ,
)+1
P1(τ,
)=
P1(τ,
)
![]() ,
,
![]()
Если поток однородный, случайный, ординарный и стационарный, то его называют простейшим или Пуассоновским.
№38 Классификация систем массового обслуживания(СМО)


 СМО
СМО
Одноканальные Многоканальные Многофазные




1-необслуженные;2-накопитель;
𝛌-
заявки; ![]() -интенсивность.
-интенсивность.
В зависимости от направления движения заявок СМО делят:

Разомкнутые Замкнутые
Если обслуженные заявки вновь отправляют на обслуживание в этой же системе, то система замкнутая. Если нет, то разомкнутая.
В зависимости от емкости накопителя СМО делят на:
1)Системы с потерями(емкость накопителя равна 0)
2)С чистым ожиданием(емкость накопителя=∞)
3)Смешанного типа(когда есть ограничения либо по длине очереди, либо по времени ожидания)
В зависимости от рода заявок (однородные, неоднородные) все системы делят на:
1)Приоритетные
2)Без приоритетные
3)Относ. приоритет
Без приоритетные – это однородные заявки, когда учитываются только моменты их поступления.
Относ. приоритет означает что поступление заявки с более высоким квалитетом она не прерывает обслуживание заявки, а без очереди поступает на канал обслуживания.
Абсолютный приоритет означает, что при поступлении заявки с таким приоритетом прерывается обслуживание заявки, канал освобождается и на него поступает заявка с абсолютным приоритетом.
При ряде допущений разработан и используется аналитический аппарат, позволяющий рассчитать вероятностные характеристики СМО.
Для всех остальных случаев математического аппарата нет.
№39 Использование ТМО для оптимизации процессов ТО и Р автомобилей.
Что бы использовать ТМО необходимо идентифицировать производственную си, как СМО, т.е. необходимо признать, что алгоритм функционирования производственный и какой-нибудь из классифицированных схем СМО одинаков.
Пост Д-1
- входной поток λ
- с чистым ожиданием
-выходной поток м
- разомкнутая система
СМО- одноканальная , разомкнутая, с чистым ожиданием, без приоритетная.
№40 Простейшие СМО с отказами.
Простейшей СМО наз если она имеет один канал, не имеет мест ожидания, на ее вход поступает простейший поток заявок с интенсивностью λ.
![]()
Число обслуживаемых заявок-m
![]()
Система
будет находится в состоянии ![]() ,
если ( в интервале времени
,
если ( в интервале времени ![]() прилегающая
к t.
прилегающая
к t.
В
момент времени t
система находится в состоянии ![]() и за интервал времени
и за интервал времени ![]() не переходит в состояние S1
(
не пришла не одна заявка)
не переходит в состояние S1
(
не пришла не одна заявка)
В момент времени t система находится в состоянии S1 , а за время не перешла в состояние ( освободился канал и не пришла ни одна заявка).
