15. Оценка точности измерений
Оценить точность измерений – определить среднеквадратичную ошибку измерений ( ) : истинное значение известно или неизвестно.
Истинное значение (а) известно:
Истинное значение (а) неизвестно:
Это точечная оценка
Ширина интервала определяется из условия, что относительное отклонение среднеквадратической ошибки измерения от эмпирического стандарта не будет превышать нормируемой величины.
16. Формулировка метода наименьших квадратов
Ставиться задача аналитического представления искомой функциональной зависимости. Нецелесообразно подбирать такую функцию, которая точно описывала бы опытные значения, поскольку при измерениях возникают случайные ошибки.
У=ax+b
Параметры a, b, c нельзя определить точно по экспериментальным значениям, поскольку эти значения имеют ошибки. Поэтому пытаются определить приближённые значения этих параметров.
Допущения:
1.измерение функций приведены независимо друг от друга;
2.ошибки измерений подчиняются нормальному закону распределения
При
определении параметров формулами (
)
используют условие, чтобы сумма квадратов
отклонений, измеренных значений
от расчётных принимало наименьшее
значение.
17. Отыскание параметров линейной ф-ии методом наименьших квадратов.
;
;
;
;
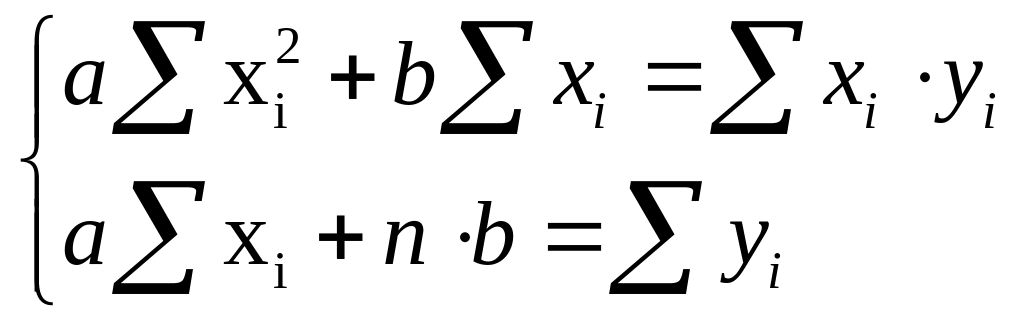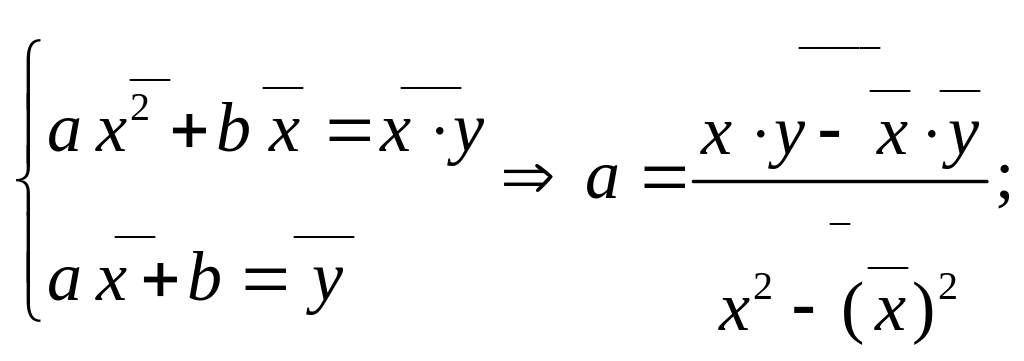
18. Отыскание параметров квадратичной ф-ии методом наименьших квадратов.
;
;
;
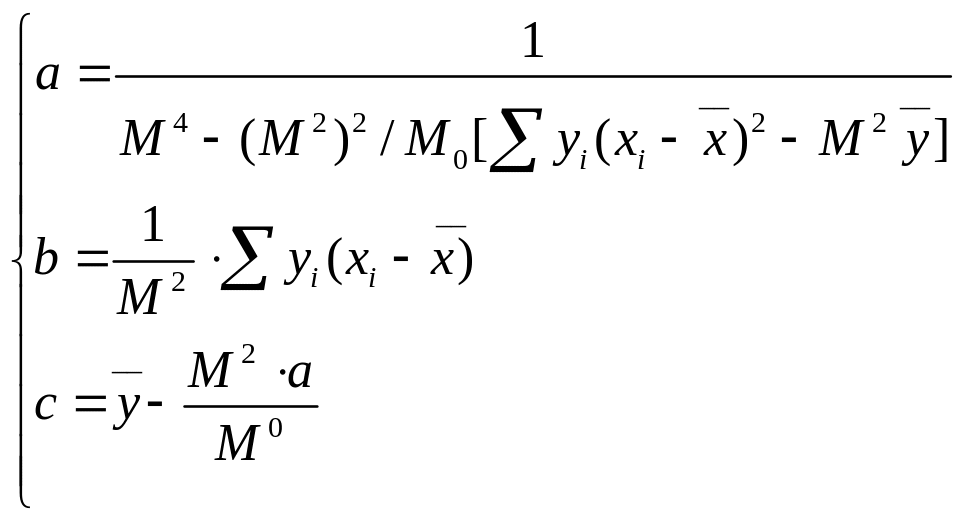
19. Приближённые и упрощённые методы отыскания параметров, входящих в формулы нелинейно
Для
отыскания значений параметров сложной
зависимости применяют методы
выравнивания,
т.е. приведение формул к более простому
виду типа 
;
;
b=A; 
;
;
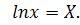
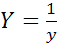Y=ax+b
20. Отыскание параметров многочлена
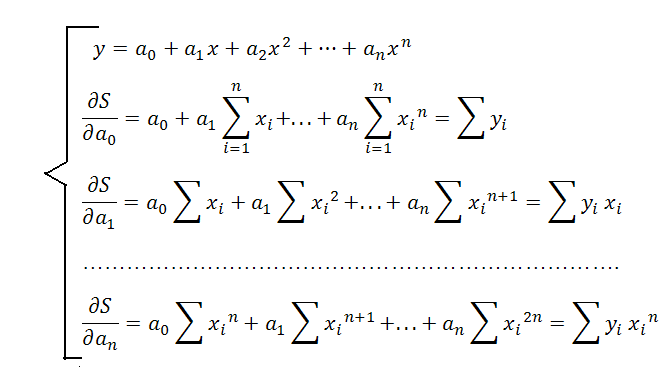
При повышении степени многочлена приходится заново рассчитывать все коэффициенты многочлена, поэтому Чебышев предложил записывать:
Чебышев решил упростить свою методику и использовать равноотстоящие значения аргументов и ввести новую переменную U.
,
i=1,n
От 5 до 25 точек.
;
;
;
;
21. Выбор оптимальной степени многочлена
При использовании малой степени многочлена экспериментальным значением описывается приближенно, если использовать большую степень, то описываются ошибки измерений.
Этапы
1)
Определяются значения 
2)
Находят сумму отклонения: 
3)
Нормируемая величина: 
4)
5)
Квадратичная зависимость: 
Степень многочлена повышается до тех пор, когда величина q перестанет сильно изменяться.
22. Сглаживание эмпирических данных
Для анализа экспериментальных зависимостей необходимо устранить “шум” и сохранить информацию об истинной информации.
Сглаживание – это замена таблицы эмпирических данных на другую таблицу с точками лежащими на достаточно гладкой кривой.
При сглаживании количество точек берут нечетное, а группы точек скользящими вдоль всей таблицы.
При сглаживании по трем точкам берут первые три значения и сглаживают среднее:
Для
крайних точек: 
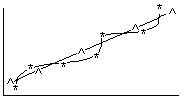
Иногда проводят повторные сглаживания, но это может сильно изменить значение, и мы отойдем от истинного значения.
№ 23 построение матрицы спектра плана полнофакторного эксперимента
В матрице спектра плана должны отсутствовать совпадающие и полностью противоположные столбцы.
Выбирают структуру уравнений регрессий и определяют степень дробности так чтобы N>n.
Выбирают ведущие факторы и строят для них матрицу спектра плана.
Оставшуюся часть матрицы спектра плана заполняют на основе генерирующих отношений, которые по своей сути есть произведение соотв. столбцов ведущих факторов.
-
восемь
силовых экспериментов
N |
|
|
|
|
1 |
- |
- |
- |
- |
2 |
- |
- |
- |
- |
3 |
- |
- |
- |
- |
4 |
- |
- |
- |
- |
5 |
- |
- |
- |
- |
6 |
- |
- |
- |
- |
7 |
- |
- |
- |
- |
8 |
- |
- |
- |
- |
n - число факторов.
№24 основные положения планирования эксперимента
Планирование эксперимента – выбор плана эксперимента из нескольких альтернативных.
План эксперимента – совокупность данных определяющих число, условие и порядок реализации.
План эксперимента задается планом варьирования факторов.
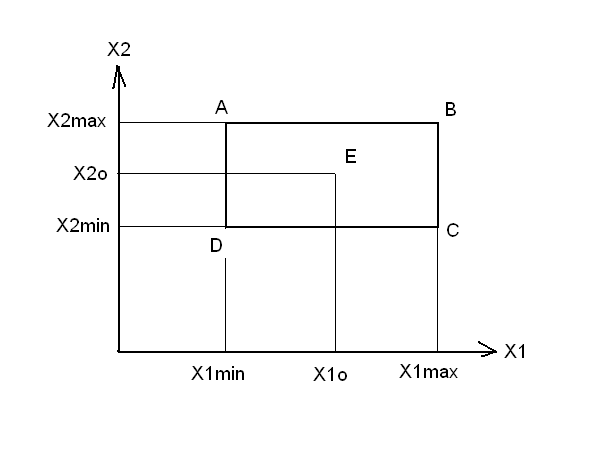
Е
– центральная точка эксперимента V=2
План эксперимента должен содержать все возможные комбинации значений всех факторов на всех уровнях их изменения. План эксперимента лучше представить в виде таблицы. По строкам идут эксперименты, а по столбцам – учитываемые при эксперименте факторы.
Min=-1, max=1 центральная точка=0
Матрица спектра планов.
N |
X1 |
X2 |
…….. |
…… |
Xn |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
2 |
+1 |
-1 |
-1 |
-1 |
-1 |
3 |
+1 |
+1 |
-1 |
-1 |
-1 |
…… |
+1 |
+1 |
+1 |
-1 |
-1 |
…… |
+1 |
+1 |
+1 |
+1 |
-1 |
n |
+1 |
+1 |
+1 |
+1 |
+1 |
В
первой строке всем факторам присваивается
значение (-1), далее таблица заполняется
по столбцам. N=3;
;
.
N |
X1 |
X2 |
X3 |
Y |
1 |
-1 |
-1 |
-1 |
Y1 |
2 |
+1 |
-1 |
-1 |
Y2 |
3 |
-1 |
+1 |
-1 |
Y3 |
4 |
+1 |
+1 |
+1 |
Y4 |
5 |
-1 |
-1 |
+1 |
… |
6 |
+1 |
-1 |
+1 |
… |
7 |
-1 |
+1 |
-1 |
… |
8 |
+1 |
+1 |
-1 |
Y8 |