Глава 12. Анализ затрат

Е сли функция общих затрат линейна или почти линейна в пределах нужного ин­тервала, то эластичность общих затрат, Е_с, может быть вычислена по формуле

	тс2	-тс[
Е	(тс2,	■ТСх)/2	тс2-	тс{		d
£С "	G2	-d.	ТС2 +	тс,	G2"

(12)

Эта формула описывает изменения средней эластичности затрат в интервале изме­нения объемов производства от Q_x до Q_r

Свойства функций краткосрочных затрат

Обобщенная функция затрат представляет собой кубическую функцию объема про­изводства

ТС= а + bQ- cQ² + dQ\ (13)

Она является обратной относительно соответствующей обобщенной кубической функции, которая описывает увеличение и последующий спад предельного продукта или отдачи на вводимый фактор. Соответственно, как следует из рис. 12.3, функция затрат также отражает увеличение и последующий спад предельных затрат. Предель­ные затраты могут быть определены по наклону любой из этих кривых, потому что формы кривых ТС и TVC одинаковы. Расстояние между ними по вертикали равно общим постоянным затратам, TFC.

= a + bQ-cQ²

Уменьшение производитель­ности

Увеличение производитель­ности

Увеличи­вающиеся МС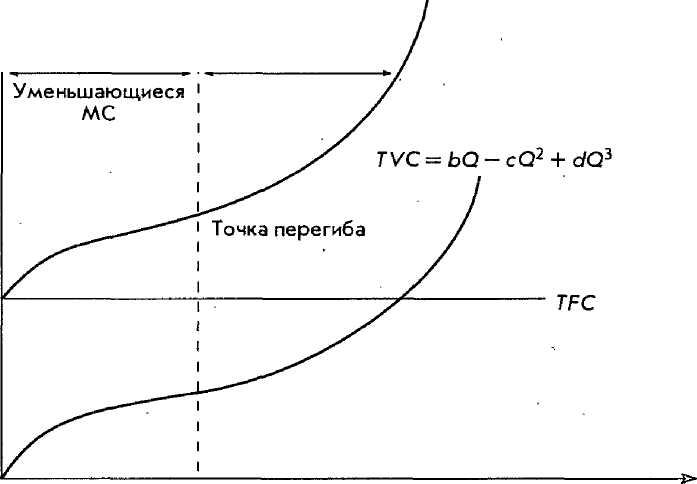

а.

с.

_I

Объем производства Рис. 12.3. Обобщенная функция краткосрочных затрат

390

Теория затрат: функции «затраты—выпуск»

К ак следует из рис. 12.3, классическая функция затрат охватывает весь интервал производительности предприятия — от нулевого объема производства, при котором TVC — 0, до максимального объема производства в условиях полного использования производственных мощностей, когда общие,затраты максимальны. Однако внутри этого интервала могут найтись участки, на которых функция линейна или почти линейна. Если это так, то характеристики подобных участков можно определить по табл. 12.2, в которой представлены математические свойства линейных, квадратичных и кубиче­ских функций затрат.

Таблица 12.2

Кривые затрат, соответствующие различным функциям затрат

Функция	Линейная	Квадратичная 1	Квадратичная II	Кубическая
ТС TFC TVC	а + bQ а bQ	а + bQ - cQ2 а bQ - cO1	а + bQ + cQ2 а bQ + cQ2	a + bQ - cQ1 + dQ3 а bQ - cQ2 + сЮъ
АТС	± +Ь Q	— + Ь - cQ Q	— + b + cQ Q	— + Ь - cQ + dQ2 Q
AFC AVC мс	а Q ь ь	а a Ь- cQ Ь - 2cQ	а Q b + cQ b + 2cQ	а Q b - cQ + dQ2 b - 2cQ + 3dQ2
£	ь	b-2cQ	b + 2cQ	b-2cQ + 3dO2
'с	а	— + b-cQ Q	—+b+cQ Q	— + b-cQ + dQ2 Q

В общем, мы можем заметить следующее.

12. Если функция затрат не была получена методом регрессионного анализа данных производства, который не охватывает низких уровней производства, то в качестве общих постоянных затрат может быть выбран постоянный параметр а. В этом слу­ чае постоянный член регрессионного уравнения не отражает постоянных затрат, а лишь соответствует оси ординат, которая служит для правильного размещения ре­ грессионной линии в выбранном интервале изменения объема производства. В любом случае при удалении из уравнения общих затрат постоянного члена остав­ шаяся часть уравнения соответствует общим переменным затратам.

13. Предельные затраты можно получить из уравнения общих затрат.

14. Величина a/Q соответствует средним постоянным затратам. Если ее убрать из урав­ нения средних общих затрат, то оставшаяся часть уравнения будет соответствовать средним переменным затратам.

15. Эластичность затрат есть отношение предельных затрат к средним общим затра­ там.

Далее обсуждаются некоторые экономические интерпретации этих математических свойств.

Линейные функции затрат. На рис. 12.4 представлены кривые затрат, соответст­вующие линейной функции, ТС - а + bQ. Как будет пояснено в следующей главе, данные эмпирических исследований показывают, что линейные функции затрат очень часто имеют фирмы, которые действуют в самых разных отраслях промыш­ленности в широком интервале изменений объемов производства, который может быть назван нормальным. Одно из объяснений" этого явления заключается в том,

, 391

Глава t2. Анализ затрат

ч то в пределах нормального интервала изменений объемов производства для каж­дого объема производства постоянные и переменные вводимые факторы могут быть скомбинированы так, чтобы обеспечить минимальные затраты. Однако если требу­ется получить функцию затрат для больших объемов производства, то линейная аппроксимация уже не подходит. Это связано с тем, что здесь не учитывается закон переменных пропорций. Иными словами, уравнение не допускает увеличения об­щих затрат, даже если объемы производства приближаются к физической производ­ственной мощности предприятия.

Область

переменных

затрат

TFC

Область

постоянных

затрат

Объем производства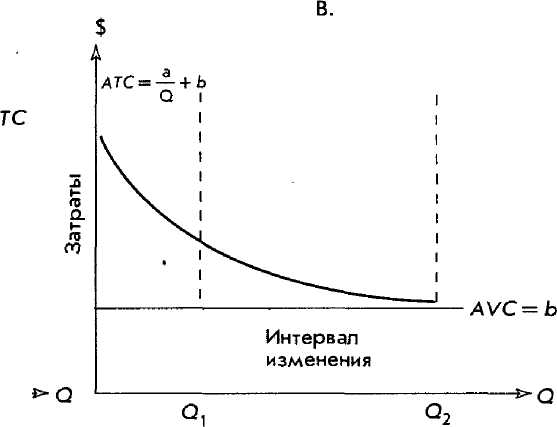

л

I-

Q. ГО

$ А

А.

Нормальный интервал изменения объемов производства

Рис. 12.4. Линейная функция затрат: ТС = a + bQ

Заметим, что средние переменные затраты (AVQ и предельные затраты (MQ по­стоянны и равны между собой. Кривая средних общих затрат (АТС) асимптотически приближается к кривой средних переменных затрат. В пределах нормального интерва­ла изменений объемов производства кривая АТС выравнивается и величина А ТС оста­ется практически постоянной.

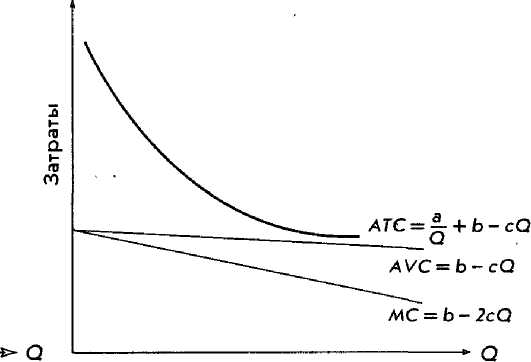
Квадратичные функции затрат. Как следует из табл. 12.2, возможно существование двух типов квадратичных функций. Первый тип описывается обобщенным уравнени­ем ТС= a + bQ — cQ². Соответствующие кривые затрат представлены на рис. 12.5. Как всегда кривая АТС асимптотически приближается к, кривой AVC. С увеличением объ­ема производства средние переменные затраты уменьшаются с постоянной скоростью, а предельные затраты уменьшаются еще быстрее. К сожалению, такая ситуация вряд ли будет наблюдаться при нормальном интервале изменения объема производства. Она может наблюдаться при вводе в действие нового производства, когда постоянные фак­торы производства являются избыточными по сравнению с переменными вводимыми факторами. Таким образом, уменьшение предельных затрат может быть связано с бо­лее эффективным использованием постоянных факторов, которые также вызывают уменьшение средних переменных затрат.

Квадратичная функция затрат второго типа описывается уравнением ТС = a + + bQ + cQ². Соответствующая кривая затрат представлена на рис. 12.6. Как пока­зано в варианте В, кривая AVC монотонно возрастает, а МС растет даже быстрее этой кривой. Так к&к кривая АТС асимптотически приближается к кривой AVCj она

392

Теория затрат: функции «затраты—выпуск»

д олжна пересекать кривую МС. Точка пересечения, в которой МС = АТС, а элас­тичность затрат равна 1, соответствует наиболее эффективному с точки зрения за­трат объему производства.

В.

TFC

AVC =

S .

го

$ Д

га О.

СО ГО

Объем производства Объем производства

Рис. 12,5. Квадратичная функция затрат: ТС — а + bQ — cQ¹

А. В.

$ -

MC =

Т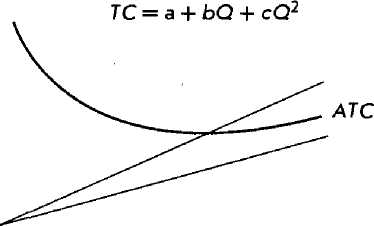 С

л

IE о.

IV

П

Область

переменных

затрат

TFC

Область

постоянных

затрат

2cQ

-*- Q

Объем производства

Объем производства

Q

Рис. 12.6. Квадратичная функция затрат: ТС = a + bQ + cQ²

Кубическая функция затрат. Обычно в учебниках по экономике в качестве ти­пичной рассматривается не линейная или квадратичная, а кубическая функция затрат типа ТС — a + bQ — cQ² + dQⁱ. Эта функция соответствует закону леремен-ных пропорций. Кривые, соответствующие такой функции затрат, представлены на рис. 12.7.

Так как функция ТС является кубической, кривые АТС и МС — квадратичные, и их значения вначале снижаются, а затем и увеличиваются. Минимуму МС, где спад пре-

393