Глава 12. Анализ затрат

A VC, спад AFC вызывает усиленный рост AVC Однако по мере увеличения объема производства мы достигаем точки, в которой увеличение AVC превышает спад AFC. В этой точке кривая А ТС устремляется вверх.

Максимум

Максимум

Переменный вводимый фактор X Цена X

МР*

ЦенаХ

^AVCQ ~ АР

Объем производства Q

А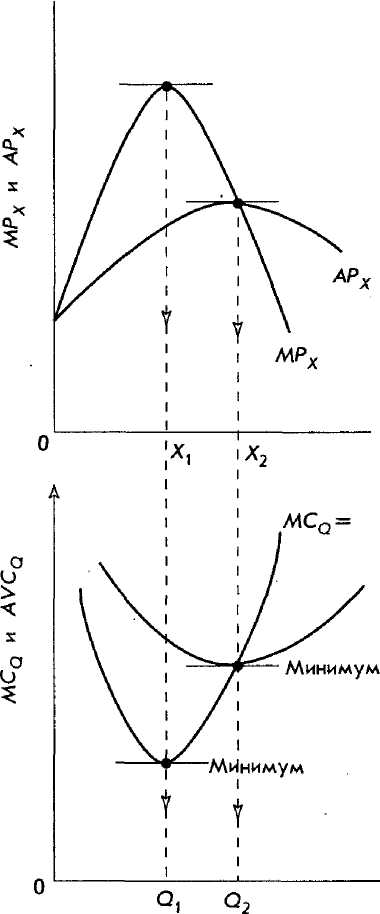

Рис. 12.2. Взаимозависимость между предельным продуктом и предельными затратами и между средним продуктом и средними переменными затратами

Ш аг 5. Наиболее экономически эффективному уровню производства соответствует точка, в которой МР_Х = АР_Х, а АР_Хпроходит через максимум. Эта точка соответствует окончанию стадии 1 и началу стадии 2 классической производственной функции, представленной на рис. 10.1 в главе 10, и совпадает с уровнем, в котором MC_Q = = AVC_U. Однако этот уровень не является наиболее экономичным или наиболее эффек­тивным с точки зрения затрат, так как здесь не учитываются средние постоянные затраты. Наиболее экономичный и эффективный с точки зрения затрат уровень про­изводства находится где-то на стадии 2, в точке, соответствующей минимуму средних полных затрат, АТС.

388

Теория затрат: функции «затраты—выпуск»

Ш шюстрат жштя *

В определенном производственном процессе для изготовления 1 изделия тре­буется затратить 5 ч и использовать сырья на 100 долл. В настоящее время уровень производства фирмы составляет 400 изделий в неделю при продолжительности ра­бочего года, составляющей 50 недель. Постоянные затраты составляют 100 000 долл. в год. Заработная плата производственного рабочего равна 12,50 долл. в час, вклю­чая налог на заработную плату, пенсионные отчисления и другие выплаты. Кроме того, каждый наемный работник имеет ежегодный оплачиваемый отпуск продол­жительностью в две недели.

Вопросы

а. Каковы средние (удельные) переменные затраты для данного производства?

б. Каковы общие удельные затраты?

Решения

а. Сначала определим общую почасовую заработную плату, включая оплачива­емый отпуск. Для каждого рабочего годовая заработная плата составляет: 52 не-депи х40чх$12,5 = $26 000. Тогда почасовая оплата равна: $26 000 : 50 рабочих недель : 40 ч = $13 в час.

Из уравнения (8) следует:

AVC_Q =

АР,

1

100

= $ 165 за изделие .

б. Годовой объем производства определяется следующим образом: 400 изделий в неделю X 50 недель = 20 000 изделий. Тогда удельные постоян­ные затраты составят

$100 000 : 20 000 изделий = $5 за изделие. Таким образом, из уравнения (10) следует:

АТС, = AFC_Q + AVC_n = $5 + $165 = $170 за изделие.

Э ластичность общих затрат. Если экономическая теория затрат изучает взаимо­связь между затратами и объемом производства, то можем ли мы определить чувстви­тельность одной переменной к изменению другой? Конечно, для ответа на этот вопрос следует использовать уже знакомое понятие эластичности.

Эластичность общих затрат служит мерой процентного изменения общих затрат, ТС, при изменении объема производства на 1%. Так, на любой точке кривой общих затрат

_ ДТС/ТС _ АТС Q _ &TC/AQ _ МС

АТС

AG ТС TC/Q

(П)

Из этого уравнения следует, что эластичность общих затрат есть отношение пре­дельных затрат к средним общим затратам.

Предположим, что эластичность затрат равна 1,2. Это означает, что если объем производства увеличивается на 1%, то полные затраты увеличиваются на 1,2%. Иными словами, при данном уровне производства, как следует из уравнения (11), предельные затраты на 20% превышают средние затраты. >

389