Глава 12. Анализ затрат

d MC dQ²

= 0,6.

Она положительна, что соответствует минимуму, в. Эластичность затрат при Q = 12 равна

MC _ 100-6Q+0,3Q² 100-6(12) + О,3(

ЮУ _ 71,2

АТС 100-3O+0,1Q² 100 - 3(i2) -+- 0,1(1 2)² 78,4

= 0,908.

Д инамика долгосрочных затрат

Как мы отмечали ранее, динамика краткосрочных затрат относится к оператив­ным понятиям. В любой данный момент времени, сейчас или в будущем, фирма управляет реальным производством, с.которым связан ряд постоянных затрат. Та­ким образом, оперативное принятие решений связано с минимизацией переменных затрат.

Напротив, понятие динамики долгосрочных затрат относится к планированию. Оно основано на предпосылке, что все вводимые факторы производства могут меняться и для каждого возможного объема производства существует такая комби­нация вводимых факторов, которая обеспечивает минимум затрат. Следовательно, для любого желаемого уровня производства возможно создать производство с опти­мальным размером.

Благодаря гибкости долгосрочных затрат фирма должна начать процесс планирова­ния с выяснения технологических и производственных методов, которые потребуются или уже имеются для расширения производства. Фирма может выбрать размер произ­водства и виды оборудования, которые лучше всего подходят для обеспечения задан­ного уровня производства. Когда фирма увеличит размер производства, некоторые производственные факторы станут постоянными. Теперь для принятия решений снова можно использовать концепцию краткосрочных затрат и, следовательно, функцию краткосрочных средних затрат.

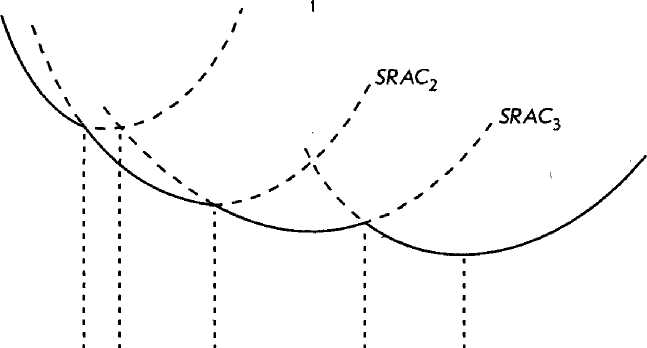
Соответствующий процесс отображен на рис. 12.8, на котором представлены кри­вые краткосрочных средних затрат для четырех предприятий, разных по размеру, каж­дое из которых обеспечивает большую эффективность, нежели предшествующее. Каж­дое предприятие наиболее эффективно функционирует при таком уровне производства, который соответствует самой нижней точке кривой, SRAC. Мы называет такой уро­вень производства проектной мощностью предприятия.

Если размер предприятия может меняться, то управляющий производством будет пытаться добиться для каждого уровня производства наименьших средних затрат. Рас­ смотрим самое маленькое предприятие. Видно, что минимум кривой краткосрочных затрат соответствует объему производства в М единиц. Однако из рисунка следует, что на втором предприятии, мощность которого выше, эти Мединиц изделий можно про­ извести с более низкими затратами. Продолжая эти рассуждения, мы придем к выводу, что производить до Q_{ изделий выгоднее всего на предприятии 1, от Q_x до Q₂ изделий - на предприятии 2, от Q₂ до (?₃ изделий — на предприятии 3, а от Q_i до Q_A изделий — на предприятии 4 (этим рассуждениям на рисунке соответствует жирная линия). Эта линия является кривой долгосрочных средних затрат, LRAС:' ■■

396

Динамика долгосрочных затрат

SRAC*

Л )

о) Ф

I

и

SRAC

Q , M

Q₂ Q₃ Q₄

Объем производства для данного периода

. 72. <У. Средние краткосрочные затраты для четырех предприятий разных размеров

Конечно, в действительности фирма может выбирать не из четырех:, а из большего количества размеров предприятия. Естественно, в зависимости от возможности деле­ния производственных единиц и их технической природы может существовать беско­нечное количество возможных размеров предприятия, каждое из которых отличается своей краткосрочной кривой средних затрат и проектной мощностью. Если соединить все точки пересечения этих кривых SRAC, то получится гладкая кривая LRAC, пред­ставленная на рис. 12.9.

SRAC,

Q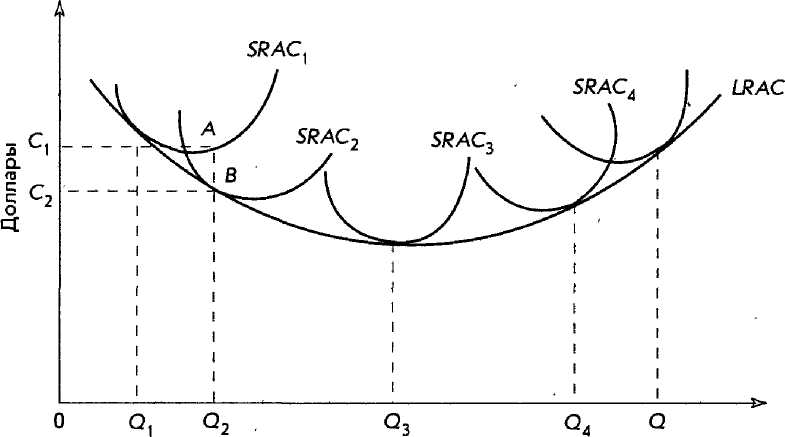

Объем производства

Рис. 12.9. Кривые краткосрочных средних затрат для предприятий разных размеров и результирующая кривая долгосрочных средних затрат

397