20 Нагрев и охлаждение электродвигателей.

Потери электроэнергии в двигателе превращаются в теплоту, вследствие чего двигатель нагревается. Отдельные части двигателя при работе нагреваются неодинаково. Выделение тепла в различных режимах также неодинаково.

Для упрощения анализа тепловых процессов, происходящих в электродвигателе, на основе ряда допущений составляют тепловые модели. Наиболее простая тепловая модель основана на следующих допущениях:

1. д 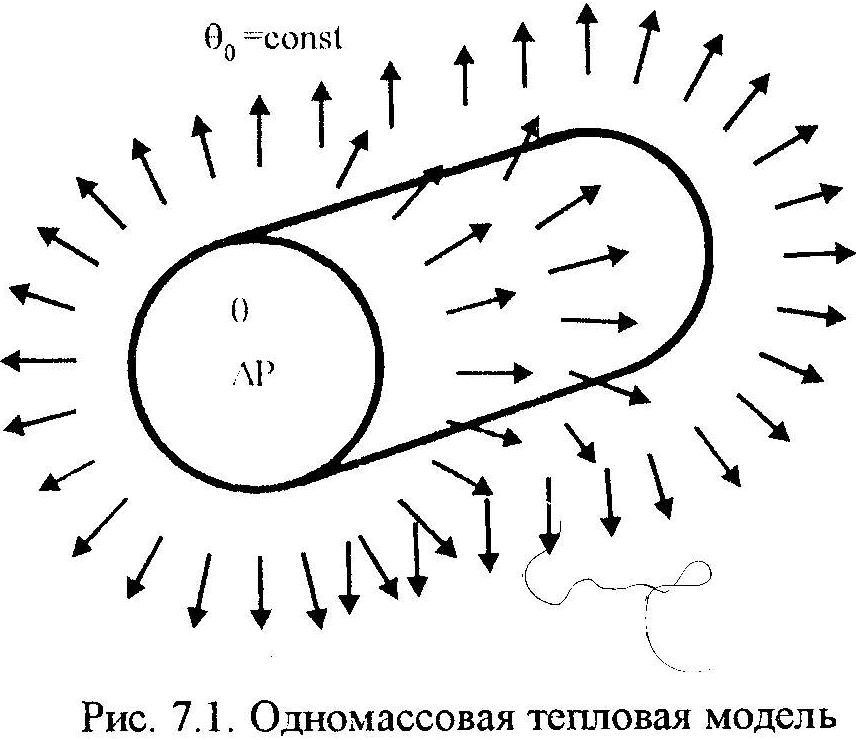вигатель представляет собой однородное в тепловом отношении тело, равномерно нагревающееся по всему объему (бесконечно большая теплопроводность) за счет источника мощности ,

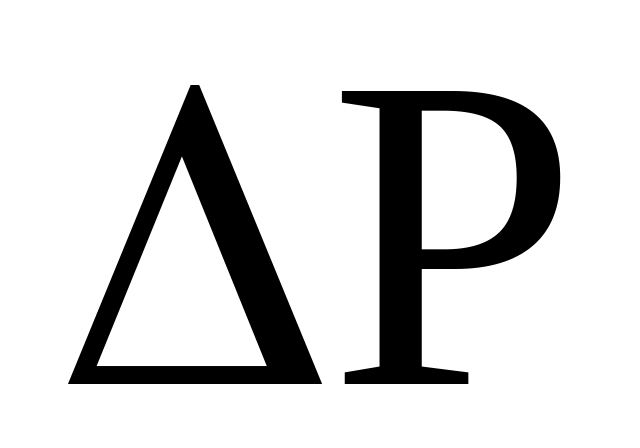2. теплоотдача во внешнюю среду пропорциональна первой степени разности температур тела и охлаждающей среды,

3. температура охлаждающей среды постоянная.

Для такой модели (Рис.7.1) мощность теплового потока, передаваемая в окружающую среду, равна , где , , - температура перегрева, ^оС; А – теплоотдача в окружающую среду, Вт/^оС; S – площадь поверхности охлаждения, м²; - удельная теплоотдача при скорости охлаждающего воздуха , Вт/^оС м²; - скорость охлаждающего воздуха, м/с; К – эмпирический коэффициент, принимаемый для электрических машин, равным примерно 0,8.

Величина, обратная теплоотдаче, называется тепловым сопротивлением Поэтому мощность теплового потока , -то,что подаётся в окружающую среду . Мощность теплового потока, идущего на нагрев тела, определяется выражением , ,

С_уд – удельная теплоемкость, Дж/^оС кг; m – масса тела, кг.

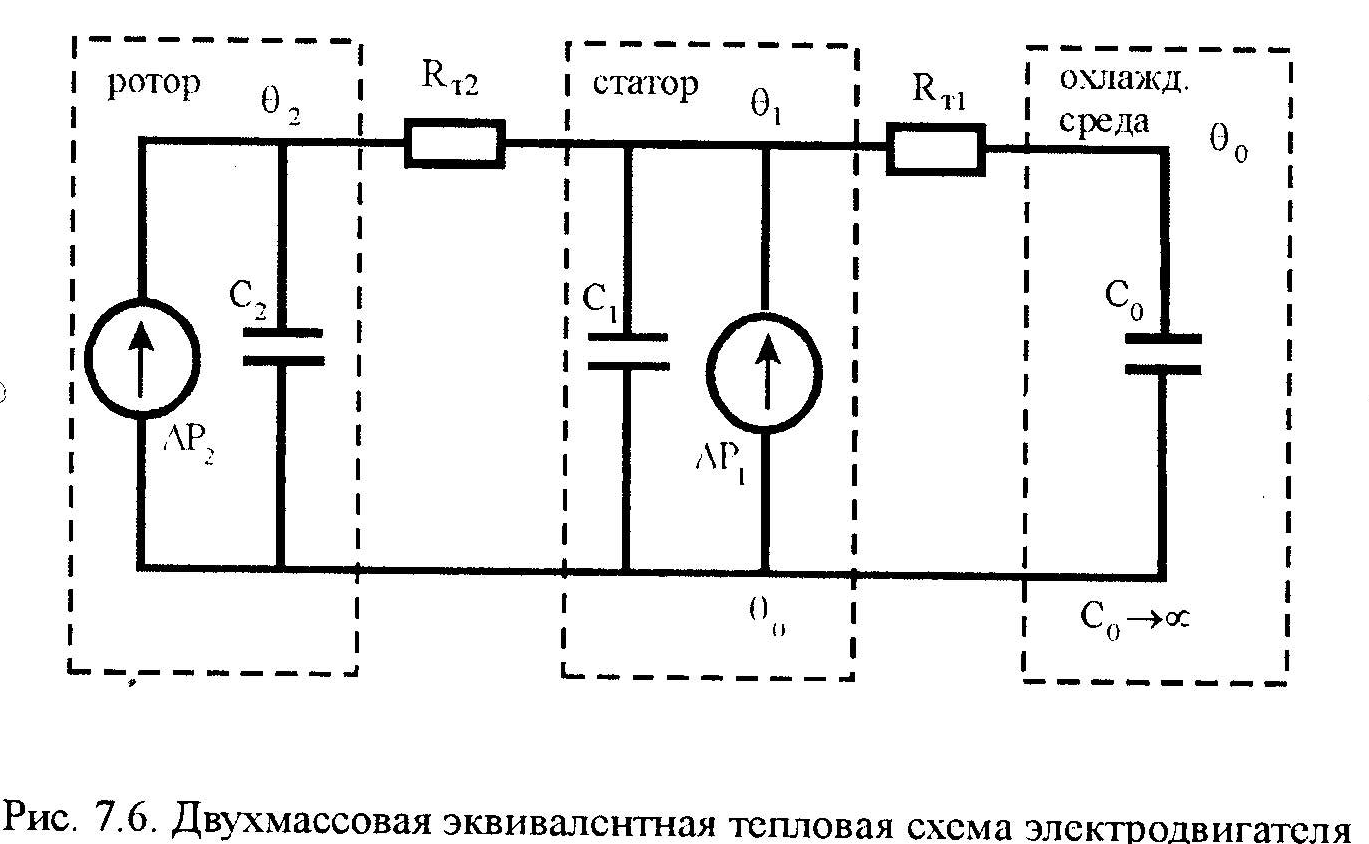По закону сохранения энергии , Или , П олученное дифференциальное уравнение теплового баланса в одномассовой модели аналогично уравнению , (7.12)

электрической цепи, показанной на Рис.7.2, где имеем аналогии: ток ~ тепловой поток , электрическое сопротивление R ~ тепловое сопротивление R_T, электрическая емкость С ~ теплоемкость с, электрический потенциал ~ температура тела , электрическое напряжение u ~ температура перегрева .

Поскольку для электрической цепи Рис.7.2 постоянная времени ,

и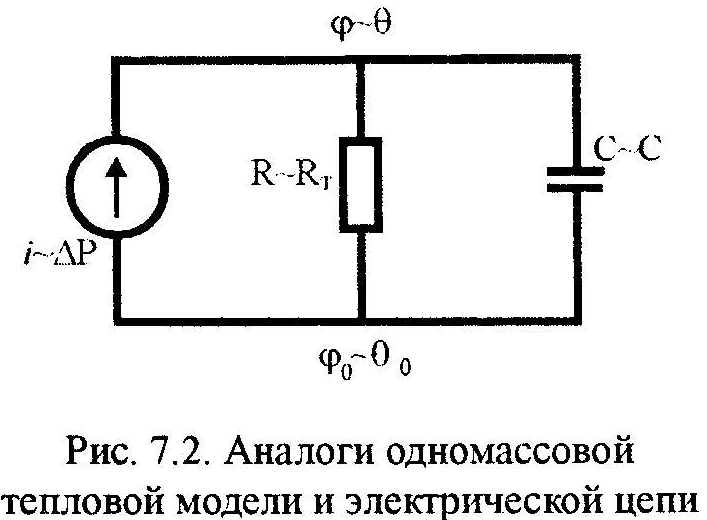 установившееся значение напряжения ,

то можно представить в виде ,

Аналогично имеем для уравнения тепловой модели , , где Т_Н – постоянная времени нагрева, - установившееся значение перегрева. , где - начальное значение температуры перегрева.

Н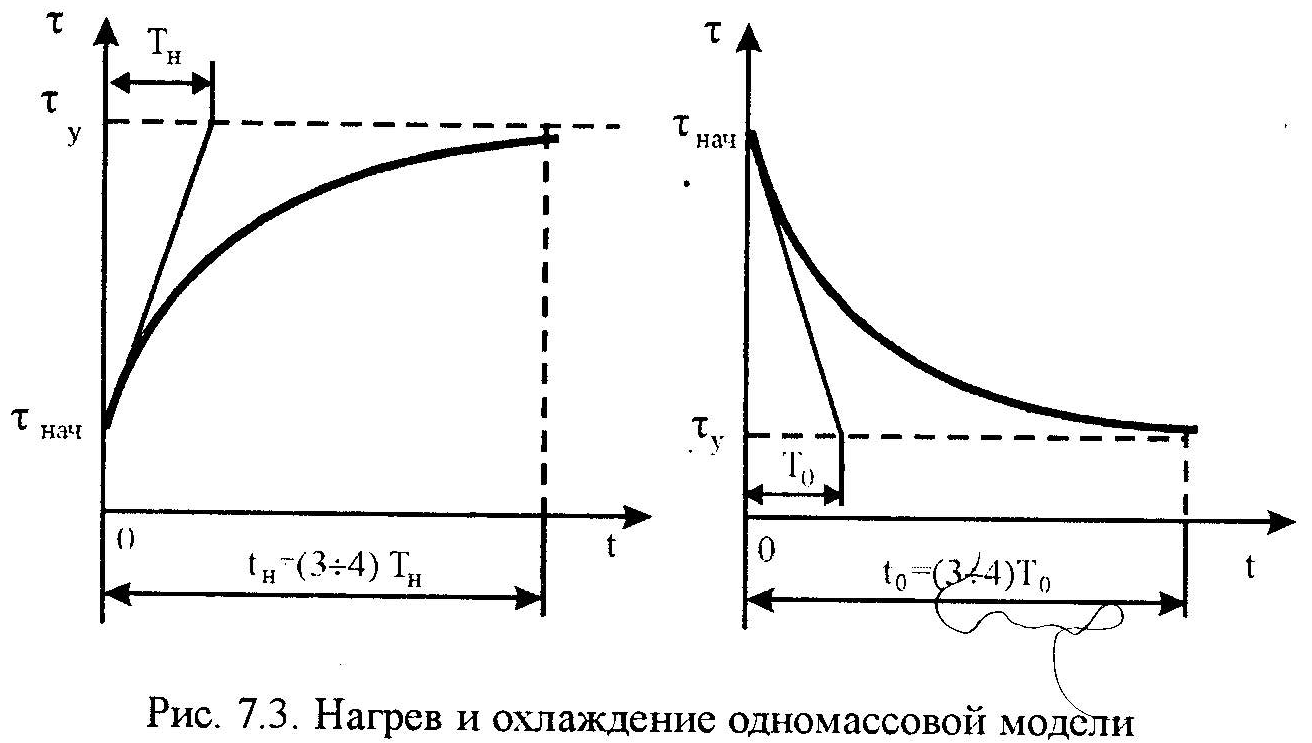 агрев или охлаждение тела определяется начальным значением температуры: если , будет нагрев, если - охлаждение

Если скорость равна 0(двигатель отключён),то

если скорость равна номинальной –то постоянной нагрева T0>Tн (вентилятор отключён,нет охл)

Если скорость постоянна ,то T0=Tн при независимой вентиляции

Одномассовая тепловая модель электродвигателя простая и удобная для анализа, но она лишь приближенно отражает нагрев обмоток. С целью повышения точности тепловых расчетов применяют двухмассовую модель, разделяя нагрев статора и ротора электродвигателя. В этом случае, принимая потери мощности в роторе и температуру внутренней поверхности статора постоянными, можем записать дифференциальное уравнение теплового равновесия ротора. -потери мощности ротора.С0-теплоёмкость среды.С1,С2-теплоёмкости статора,ротора..

Для установившегося состояния уравнение эквивалентной тепловой схемы имеет вид , где - средние температуры в точках Х и Y, - тепловой поток между точками Х и Y, R_xy – тепловое сопротивление между точками X и Y схемы.

Уравнения составляют для всех частей электродвигателя. Решение полученной системы уравнений, т.е. определение установившихся температур в разных точках эквивалентной схемы, возможно, если заранее определены тепловые сопротивления.

Уравнение Пуассона:

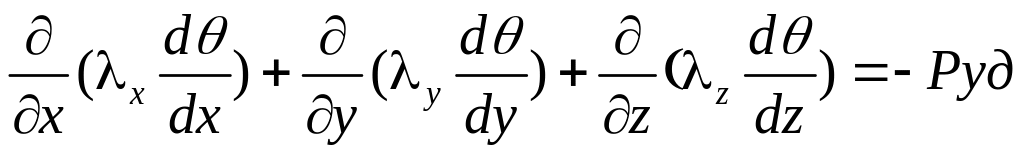
, , -удельные теплопроводности по осям х,у,z =ΔPэл/Vэл Ухудшение условий охлаждения для самовентилируемого двигателя:

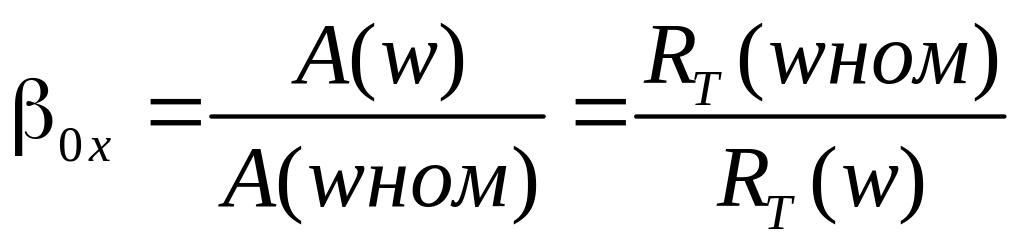
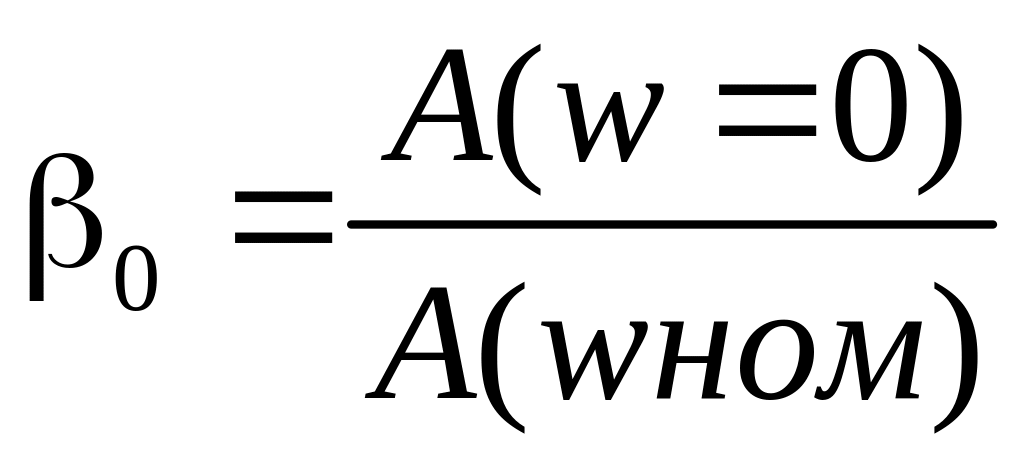
Для самовентилируемого

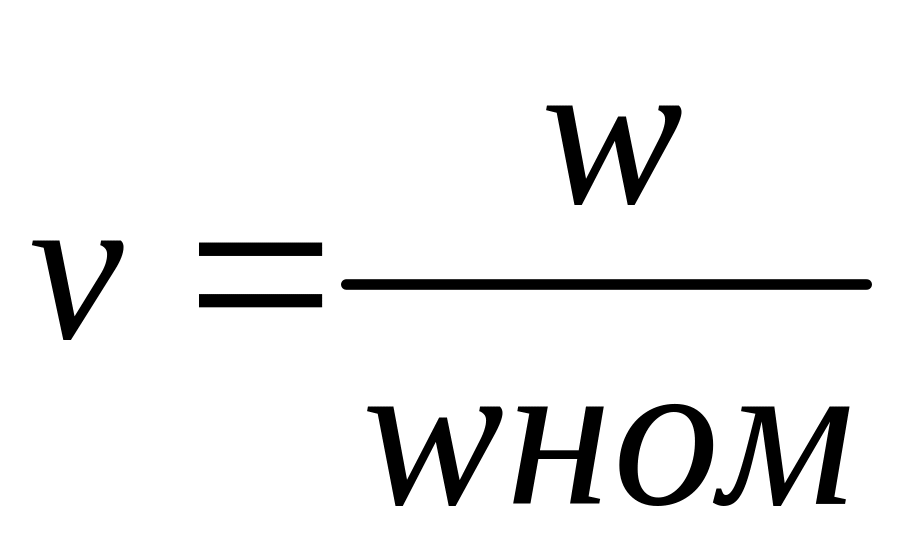
β0=1-независимое охлаждение

β0=0,95-0,98-естественное охлаждение β0=0,45-0,55-закрытое исполнение

β0=0,25-0,35-защищённое исполнение