38 Скалярное частотное управление ад при стабилизации абсолютного скольжения.

При управлении асинхронным двигателем по закону М.П. Костенко: (8.99)

а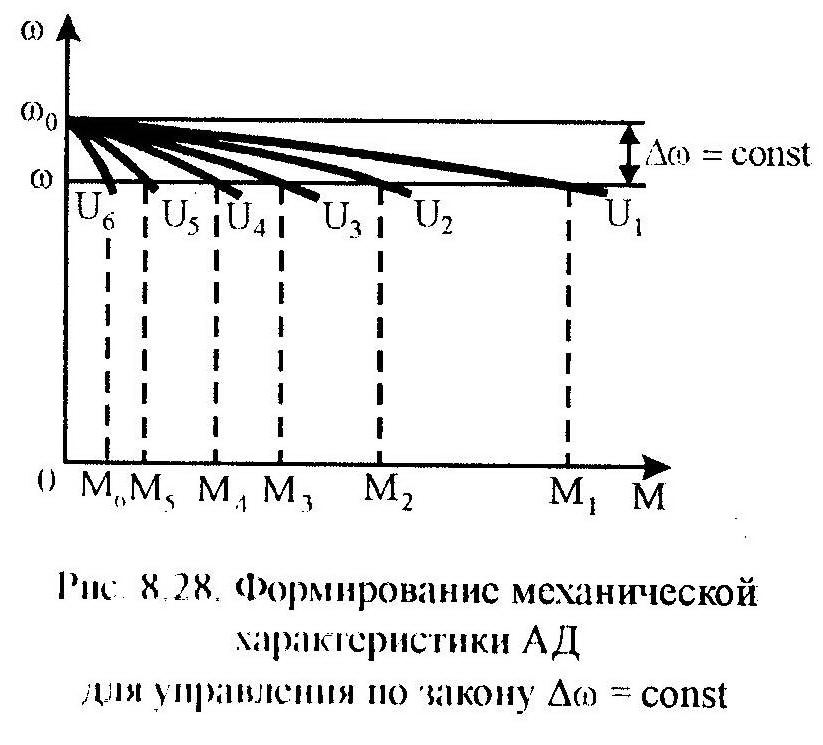 бсолютное скольжение остается практически неизменным. Отсюда следует, что если на всех частотах поддерживать абсолютное скольжение неизменным, то режим работы АД будет близок к режиму при управлении по (8.99).

Скорость АД: (8.236)

при =const и данном α будет постоянной при изменении нагрузки, поскольку каждому значению момент М соответствует своя величина напряжения U (см. рис. 8.28).

Рассмотрим функциональную схему реализации частотного управления при =const (рис. 8.29), соответствующую следующим соотношениям:

(8.237) (8.238)

где – заданное значение угловой скорости АД, – заданное абсолютное скольжение – заданное значение синхронной угловой скорости АД, которое определяет задающую частоту .

В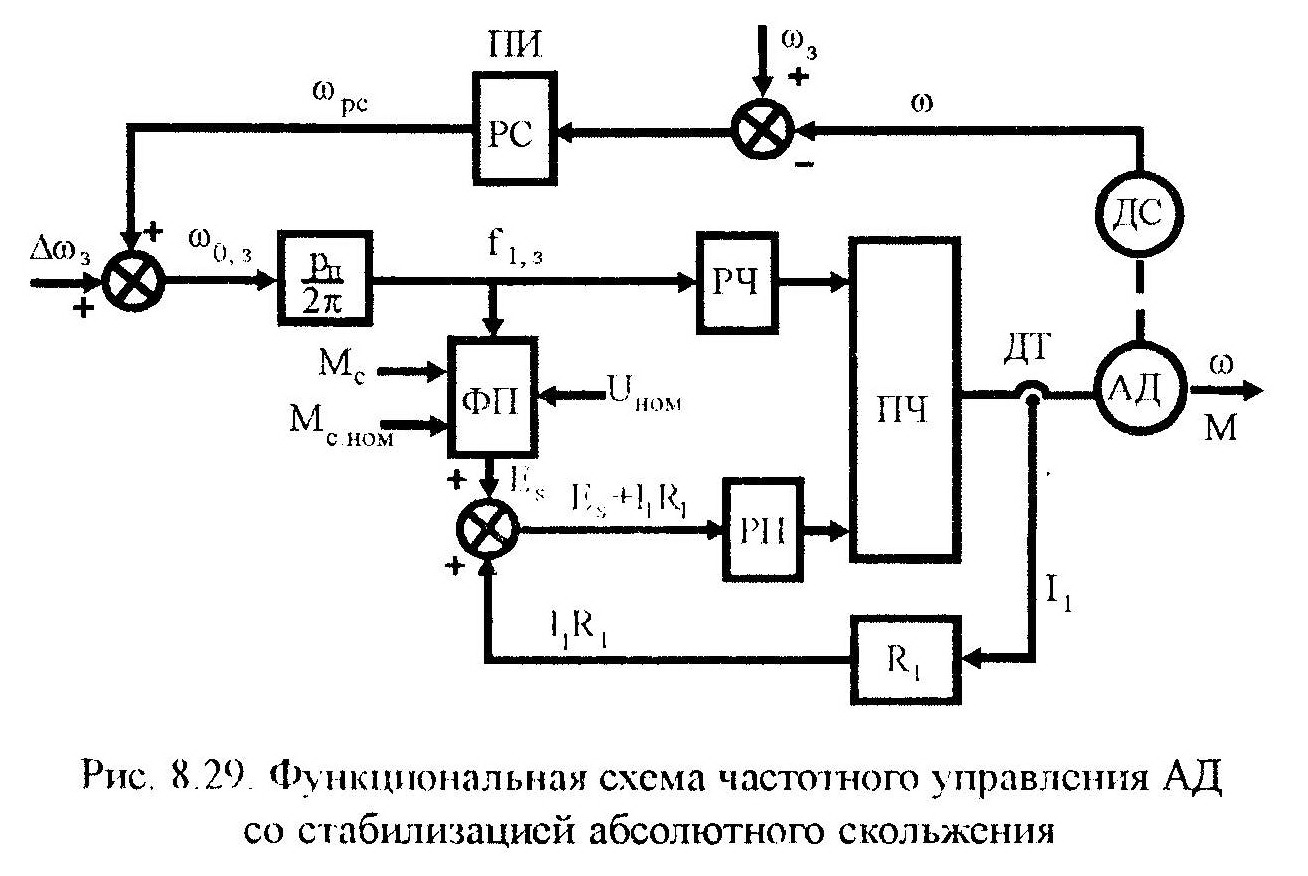 данной системе частотного управления АД с помощью датчика скорости ДС измеряется угловая скорость ω двигателя, которая сравнивается с заданным значением и их разность Δω направляется в ПИ-регулятор скорости РС, выходная величина которого суммируется с заданным падением скорости , формируя заданное значение синхронной угловой скорости и соответственно частоты .

Функциональный преобразователь ФП на основе информации о номинальном напряжении U_ном, номинальном моменте М_ном (или номинальном токе), текущем статическом моменте (или токе статора) формирует в соответствии с (8.238) значение ЭДС статора Е_s, которая суммируется с падением напряжения I₁R₁, определяя выходное напряжение U преобразователя частоты ПЧ.

В установившемся режиме = и механические характеристики АД соответствуют (8.236).

В рассмотренных системах частотного управления АД величины переменного тока принимались синусоидальными. В реальных системах ПЧ-АД выходное напряжение преобразователя несинусоидальное, поэтому все законы частотного управления и соотношения между величинами будут справедливы применительно к первым (основным) гармоникам несинусоидальных периодических величин.

39. Скалярное частотно-токовое управление ад.

При частотно-токовом управлении (ЧТУ) асинхронным двигателем управляющими величинами являются частота и величина тока статора

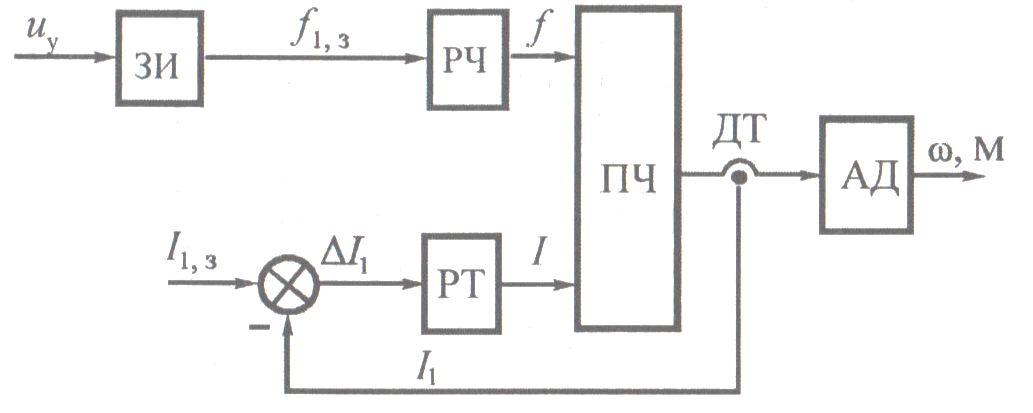
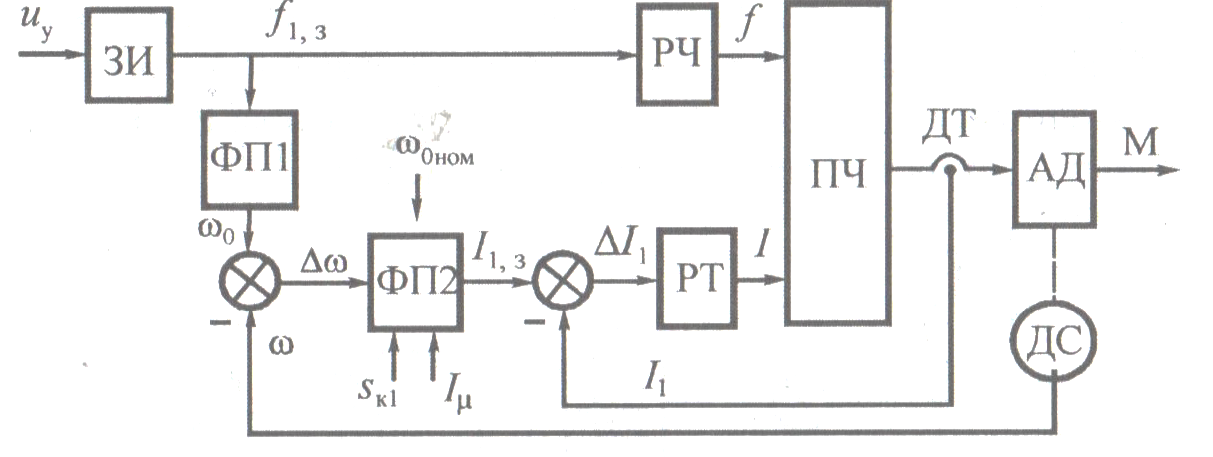
Рис 1.1. Функциональная схема разомкнутой системы ЧТУ.

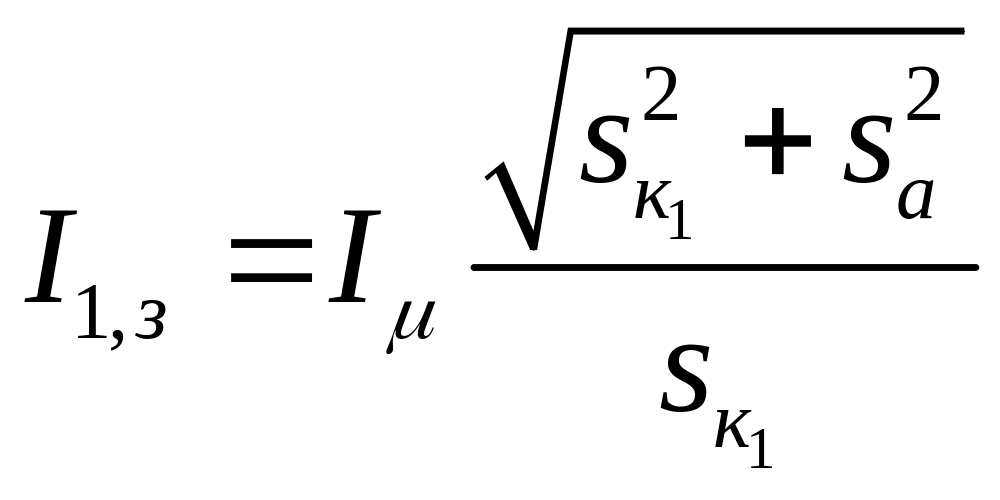
, где .

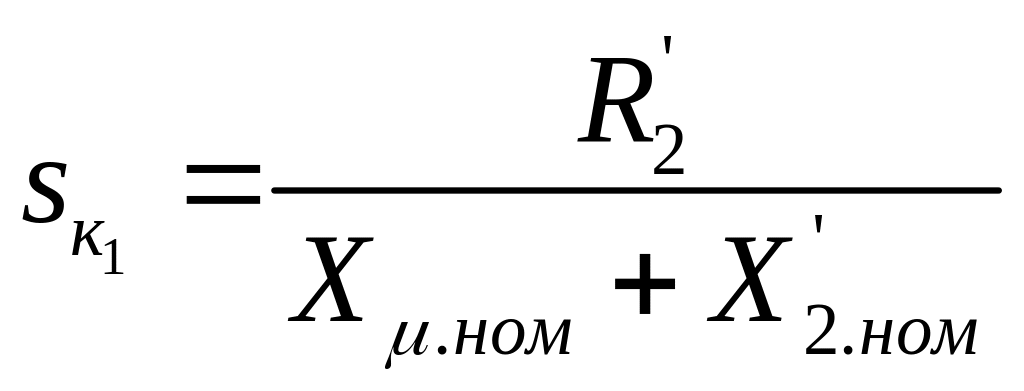Ном.ток изм. по опред.зак. илистабил.

на опред.уровне

Рис. 1.2. Функциональная схема ЧТУ со стабилизацией потокосцепления.

Д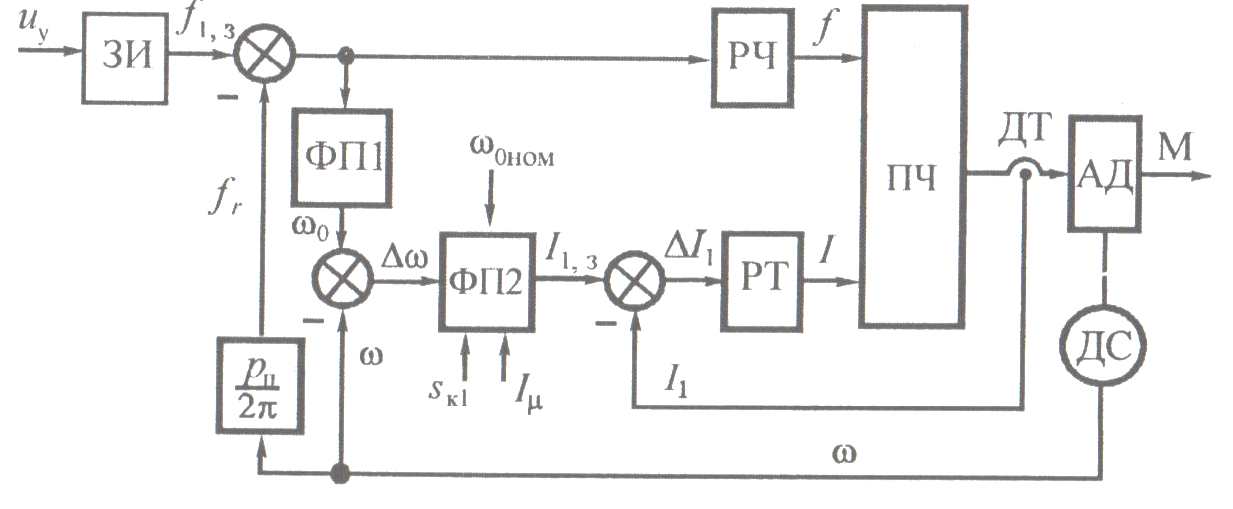 ля расширения диапозона регулирования скорости АД применяют обратную связь по скорости

Рис 1.3. Функциональная схема ЧТУ с обратной связью по скорости.

40.Рекуперативное и резистивное торможение частотно-управляемых эп

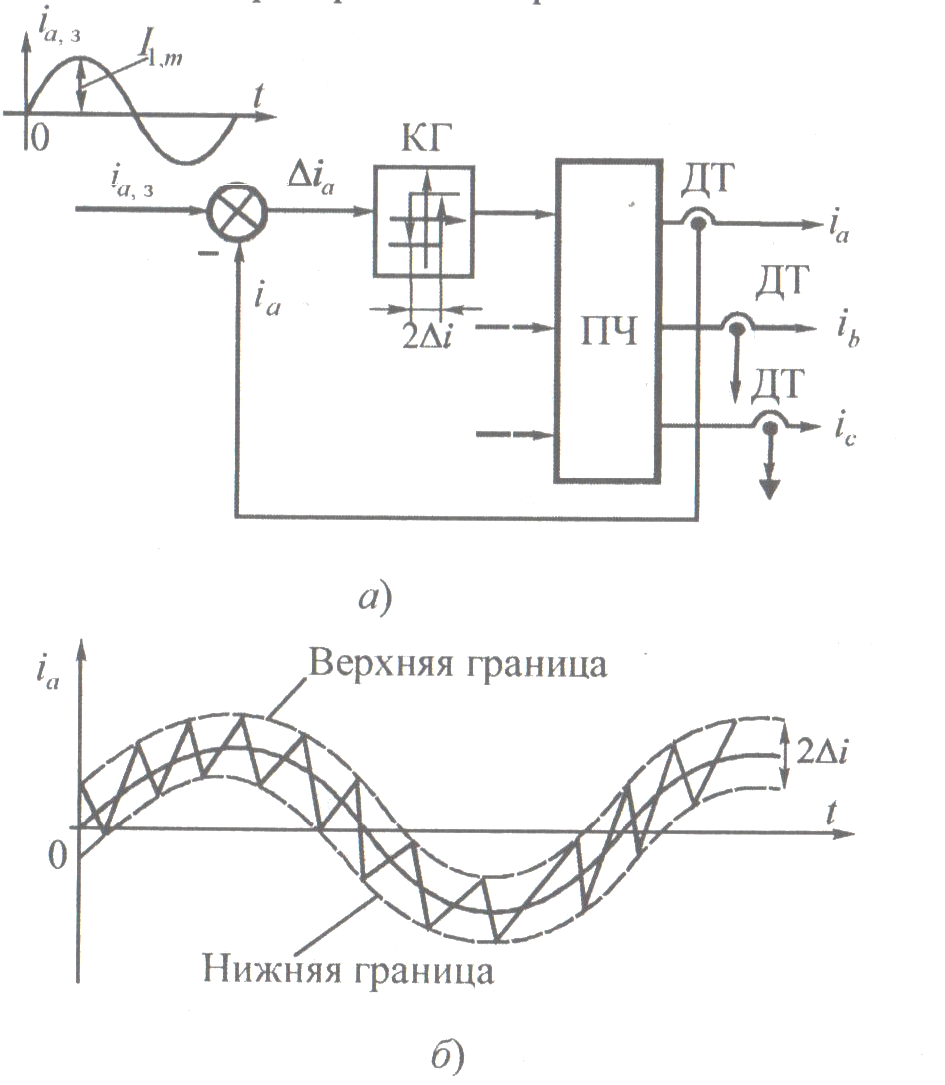
Резестивное – рекуп., энергия не в сеть, а рассеивается на тормозных сопротивлениях. Без доп технических средств рекуп торм возможно: 1)Циклоконвертор – АД(НПЧ-АД); 2)Управляемый выпрямитель – автономный инвертор тока – асинхронный двигатель.

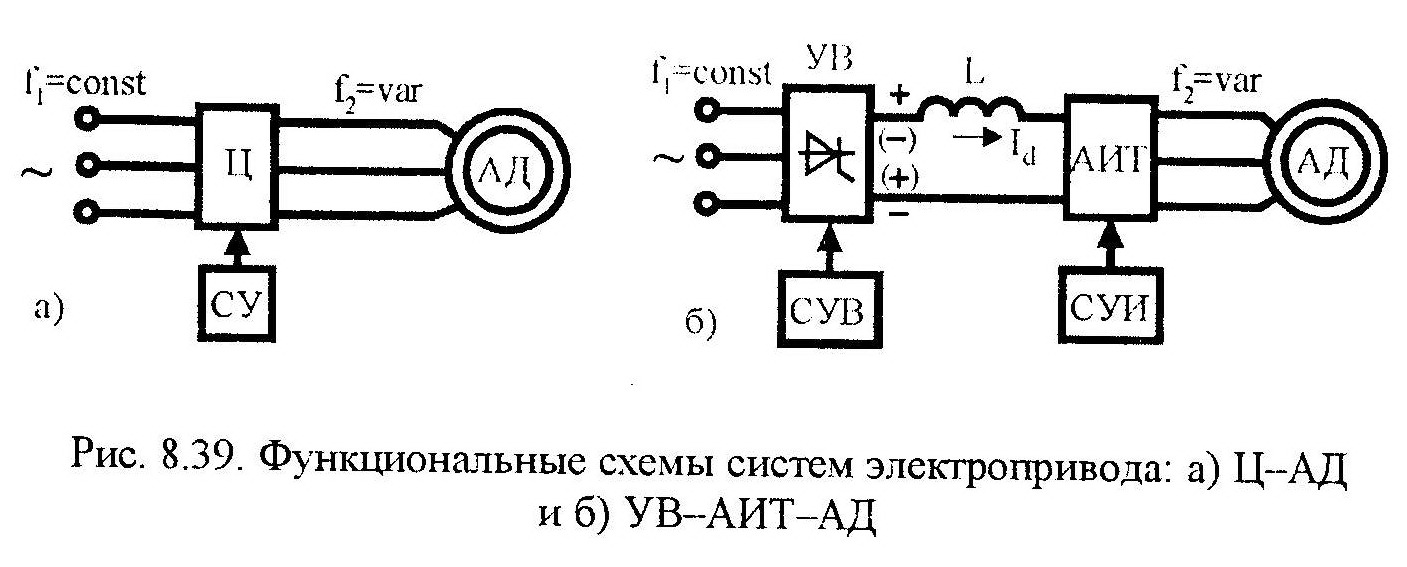
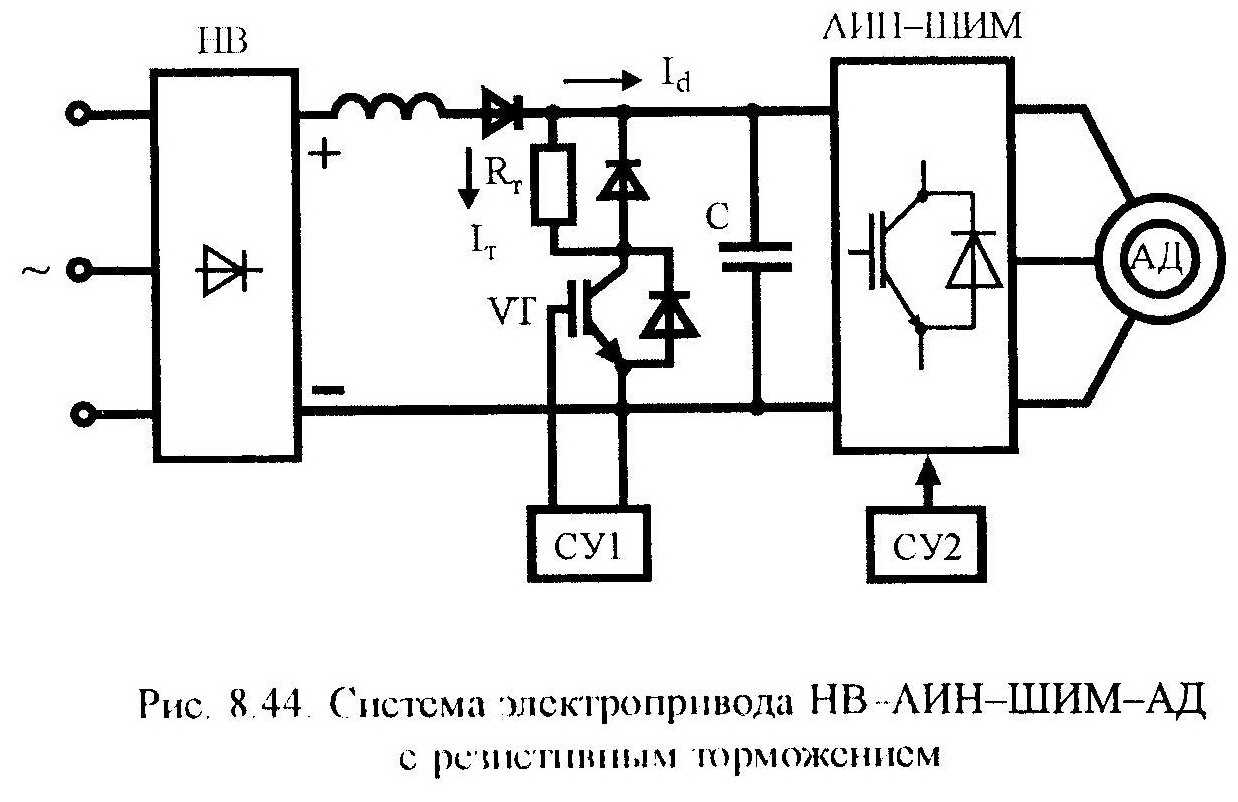
Р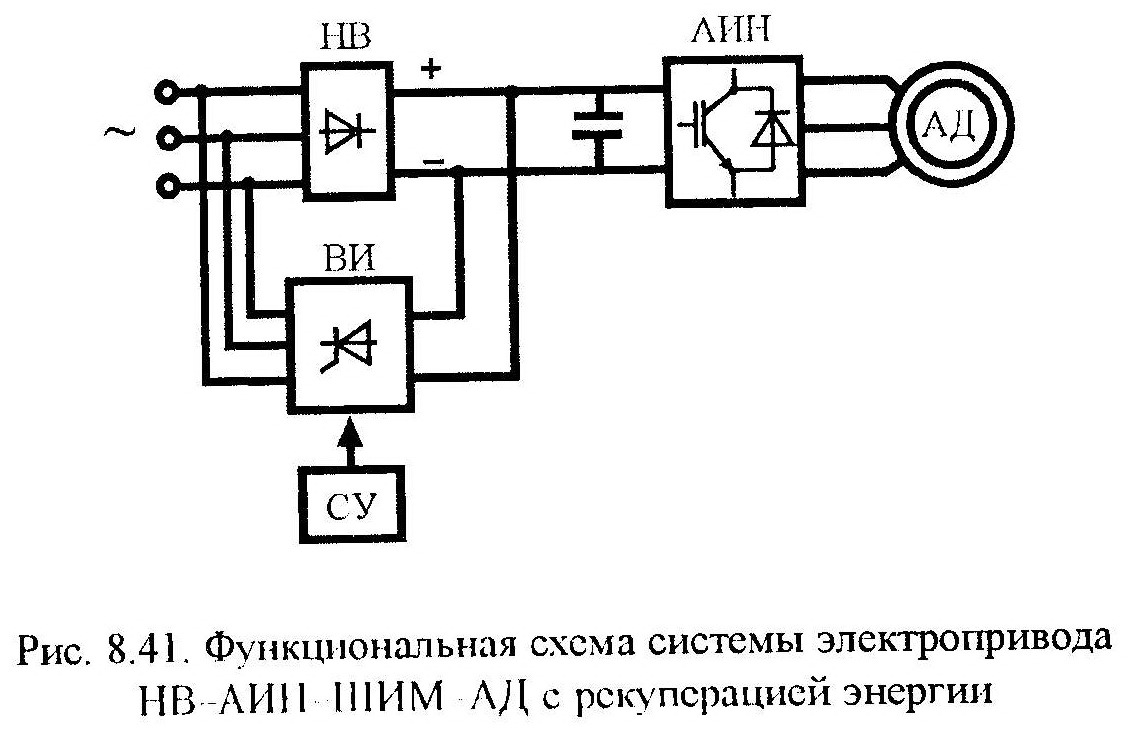 езистивное торможение.При торможении кинетическая энергия, освобождаемая инерционными массами электропривода при снижении скорости, рассеивается в виде потерь в АД, АИН и тормозном сопротивлении R_т:

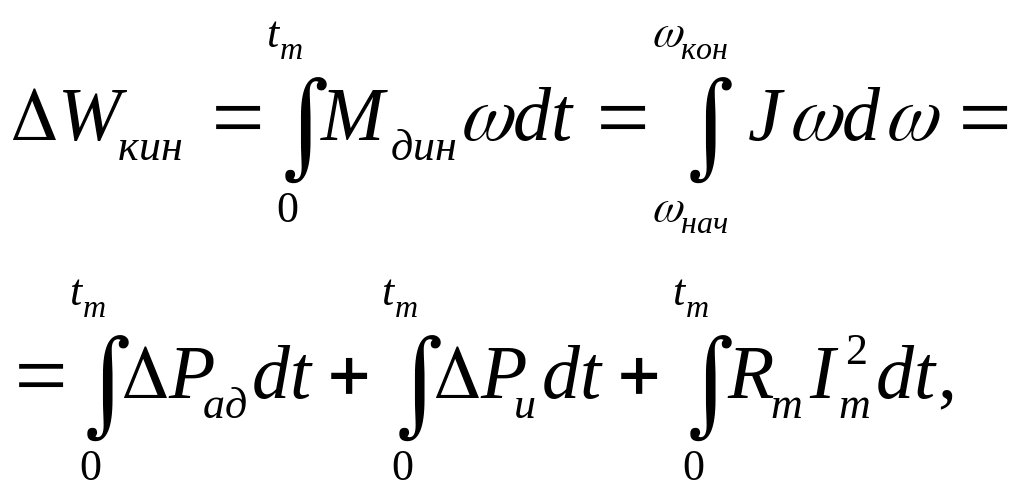
Изменение эл энергии в конденсаторе С фильтра выпрямителя:

Коэффициент мощности k_м входной цепи НВ-АИН определяется выражением

k_м=k_Icosφ₍₁₎=k_I , где

Если не учитывать индуктивности на входе НВ и принять идеально сглаженный выпрямленный ток I_d, то для трехфазной мостовой схемы выпрямления имеем следующие соотношения: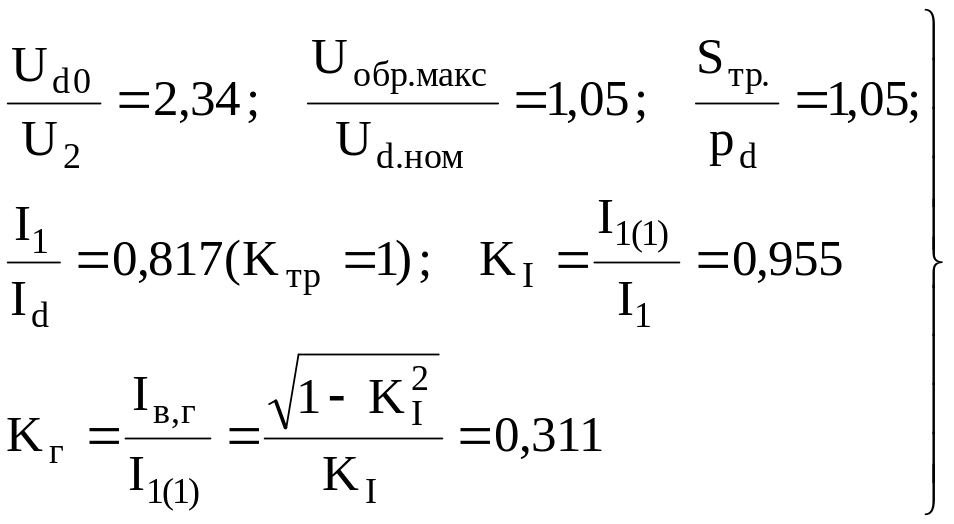