
- •Механические и электромеханические характеристики ад с кз при переменных параметрах
- •Математическая модель, характеристики и свойства синхронного двигателя
- •3) Динамические свойства синхронного двигателя при линеаризации угловой характеристики.
- •4) Взаимосвязанный электропривод при механическом соединении валов.
- •Взаимосвязанный электропривод с электрическим валом
- •6) Переходные процессы в электроприводе: общие сведенья.
- •8. Электромеханические переходные процессы при набросе и сбросе нагрузки электропривода
- •9 Переходные процессы электропривода с линейной механической характеристикой при линейном задании скорости идеального холостого хода
- •10 Переходные процессы в цепях возбуждения машин
- •11.Переходные процессы электропривода с учётом нелинейности механической характеристики.
- •12. Электромеханические переходные процессы электропривода с асинхронным короткозамкнутым двигателем.
- •13 Потери мощности в установившихся режимах работы нерегулируемых и регулируемых электроприводов
- •14 Кпд и коэффициент мощности нерегулируемого электропривода
- •15. К.П.Д. И коэффициент мощности регулируемого электропривода.
- •18 Потери энергии в переходных процессах электропривода при линейном задании скорости
- •Потери энергии за время переходного процесса ,
- •19 Выбор электродвигателей: общие сведения.
- •20 Нагрев и охлаждение электродвигателей.
- •21 Номинальные режимы работы электродвигателей.
- •22 Нагрузочные диаграммы механизма и электропривода. Выбор мощности эд по нагрузочным диаграммам
- •23 Выбор мощности электродвигателей для длительного режима работы
- •24 Выбор мощности электродвигателей для продолжительного режима работы с переменной нагрузкой методом средних потерь.
- •Для номинального режима можно записать аналогичное равенство , (7.104)
- •При переходе к пределам в (7.118) получаем
- •Продифференцировав (7.122), получим , откуда
- •25. Выбор мощности электродвигателей для кратковременного режима работы s2.
- •26. Выбор мощности электродвигателей для повторно-кратковременного режима работы (s3-s5).
- •27 Определение допустимого числа включений асинхронного двигателя с короткозамкнутым ротором.
- •28 Выбор мощности электродвигателей при ударной нагрузке электропривода.
- •.Регулирование координат электропривода.
- •30 Способы регулирования скорости электродвигателей.
- •31 Регулирование скорости ад в системах рн-ад
- •Обозначим (8.42) (8.43)
- •30(2) Ступенчатое реостатное регулирование скорости ад.
- •31 (2) Регулирование скорости ад в системе ирс-ад
- •На основании приведенной на рис.8.9 схемы системы ирс – ад имеем (8.78)
- •Подставляя (8.78) в (8.77), а затем в (8.75), получим
- •Обозначим (8.81) (8.82)
- •Для трехфазной мостовой схемы выпрямления (8.90) / тогда (8.91)
- •32 Закон костенко при частотном управлении идеализированного ад.
- •33 Влияние активного сопротивления r1 на свойства и характеристики ад при частотном управлении
- •34 Замкнутые системы скалярногочастотного управления ад.
- •Критический (максимальный ) электромагнитный момент :
- •38 Скалярное частотное управление ад при стабилизации абсолютного скольжения.
- •39. Скалярное частотно-токовое управление ад.
- •40.Рекуперативное и резистивное торможение частотно-управляемых эп
- •41 Расчёт резисторов для резистивного торможения ад
- •42 Регулирование скорости ад в каскадных схемах.
- •43. Машинно-вентильный каскад, его свойства и характеристики .
- •44. Асинхронно-вентильный (электрический) каскад, его свойства и х арактеристики.
- •Динамические свойства синхронного двигателя при линеаризации угловой характеристики.
- •Взаимосвязанный электропривод при механическом соединении валов.
6) Переходные процессы в электроприводе: общие сведенья.
Любая
физическая система, в том числе система
электропривода, содержащая один или
несколько источников энергии, называется
динамической системой. Переход
динамической системы из одного
установившегося состояния в другое
осуществляется за конечный промежуток
времени. Интенсивность изменения энергии
в переходном процессе характеризуется
величиной, которая называется постоянной
времени. С энергетической точки зрения
постоянную времени T
можно представить как отношение изменения
энергии ∆Wза
малый промежуток времени к изменению
мощности ∆P:![]()
Исходя из такого определения мы можем определить постоянную времени для указанных 4 видов.
Механический.
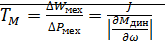 Если
Если
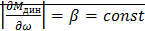 ,то тогда
,то тогда 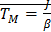 .
.Магнитный.
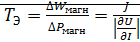 Если
Если 
Электрический.
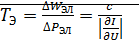 Если
Если
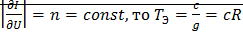
Тепловой.
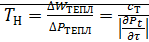
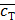 - Дж/ºС,
- Дж/ºС, 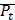 - Вт;
- Вт; 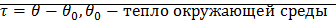 Если
Если
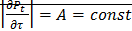
A
– Теплоотдача Вт/ºС ![]()
В зависимости от учета числа инерционностей электропривода переходные процессы разделяют на:
Механический переходной процесс
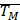
Электромеханический переходной процесс
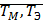 .
.
В
механических переходных процессах
учитывается только одна постоянная
времени – электромеханическая
.
Рассмотренный переходной процесс
возможен тогда, когда ![]() ,
например, при реостатном пуске двигателя
постоянного тока или асинхронного
двигателя с фазным ротором, а также в
электроприводах с большими инерционными
массами (центрифуги, дробилки, механизм
передвижения крана и т.п.).
,
например, при реостатном пуске двигателя
постоянного тока или асинхронного
двигателя с фазным ротором, а также в
электроприводах с большими инерционными
массами (центрифуги, дробилки, механизм
передвижения крана и т.п.).
В
электромеханических переходных процессах
учитываются 2 постоянные времени:
электромеханическая
и электромагнитная(электрическая)![]() .
Такие переходные процессы происходят
при прямом пуске двигателя постоянного
тока и асинхронного двигателя с
короткозамкнутым ротором, при набросе
(сбросе) нагрузки двигателя, работающего
на естественной характеристике.
.
Такие переходные процессы происходят
при прямом пуске двигателя постоянного
тока и асинхронного двигателя с
короткозамкнутым ротором, при набросе
(сбросе) нагрузки двигателя, работающего
на естественной характеристике.
Кроме того, вид переходного процесса электропривода будет зависеть от характера изменения во времени управляющего или возмущающего воздействий. В большинстве случаев возмущающее воздействие (нагрузка) изменяется скачком и определяется технологическим процессом машины(механизма), приводимой в движение электроприводом.
Целью расчета переходного процесса электропривода является получение зависимостей скорости ω,момента M и тока I и других величин от времени t для одно- и/или двухмассовой модели электропривода.
При расчете переходных процессов считают известными:
Начальные значения:
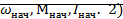 Конечные
значения:
Конечные
значения: 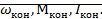
3)Закон изменения управляющего (возмущающего) воздействия.4) Параметры электропривода.
В результате подсчет переходного процесса можно оценить:
1)Соответствие характера переходного процесса требованиям, предъявляемым к механизму (допустимое, перерегулирование, колебательность, время переходного процесса).
2)Определение максимальные значения момента и тока, позволяющие проверить двигатель и силовой преобразователь по перегрузочной способности.
3)Проверить предварительно выбранный двигатель по нагреву.
4)Выбрать аппаратуру управления.
7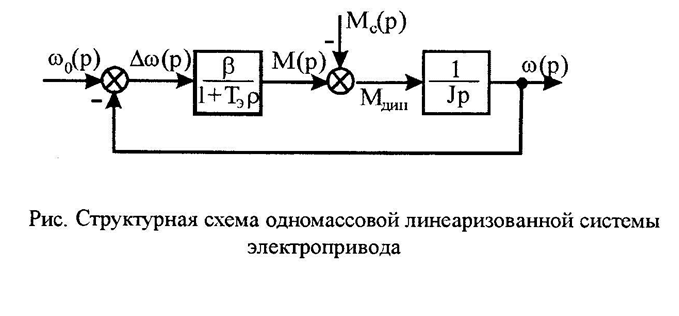 .ЭЛЕКТРОМЕХАНИЧЕСКИЕ
ПЕРЕХОДНЫЕ ПРОЦЕССЫ ЭЛЕКТРОПРИВОДА С
ЛИНЕЙНОЙ МЕХАНИЧЕСКОЙ ХАРАКТЕРИСТИКОЙ
И МС=CONST
ПРИ СТУПЕНЧАТОМ ВОЗДЕЙСТВИИ.
.ЭЛЕКТРОМЕХАНИЧЕСКИЕ
ПЕРЕХОДНЫЕ ПРОЦЕССЫ ЭЛЕКТРОПРИВОДА С
ЛИНЕЙНОЙ МЕХАНИЧЕСКОЙ ХАРАКТЕРИСТИКОЙ
И МС=CONST
ПРИ СТУПЕНЧАТОМ ВОЗДЕЙСТВИИ.
При ступенчатом управляющем (возмущающем) воздействии угловая скорость идеального холостого хода о остается неизменной (о=const), а линейность механической характеристики обеспечивает постоянство жесткости этой характеристики. Структурная схема электропривода при указанных условиях показана на рис.4.1. На основании исходных уравнений этой системы
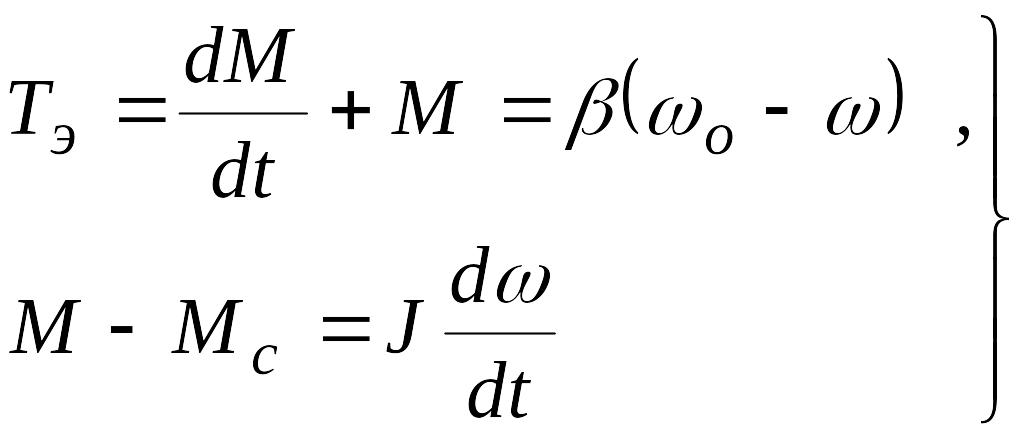 дифференциальные
уравнения для угловой скорости
дифференциальные
уравнения для угловой скорости![]() (1)и
электромагнитного момента
(1)и
электромагнитного момента
![]() где
где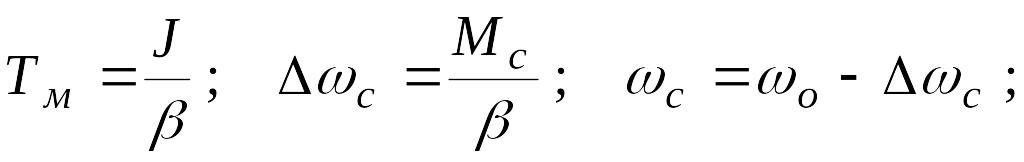 с
статическое падение скорости,
с
статическое падение скорости,
Мс , с статический момент и статическая скорость электродвигателя.
Характеристическое
уравнение
![]()
этих двух дифференциальных уравнений имеет корни
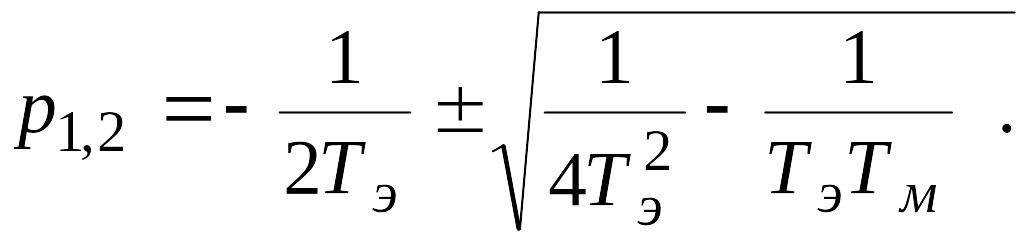 Если
обозначить
Если
обозначить
![]()
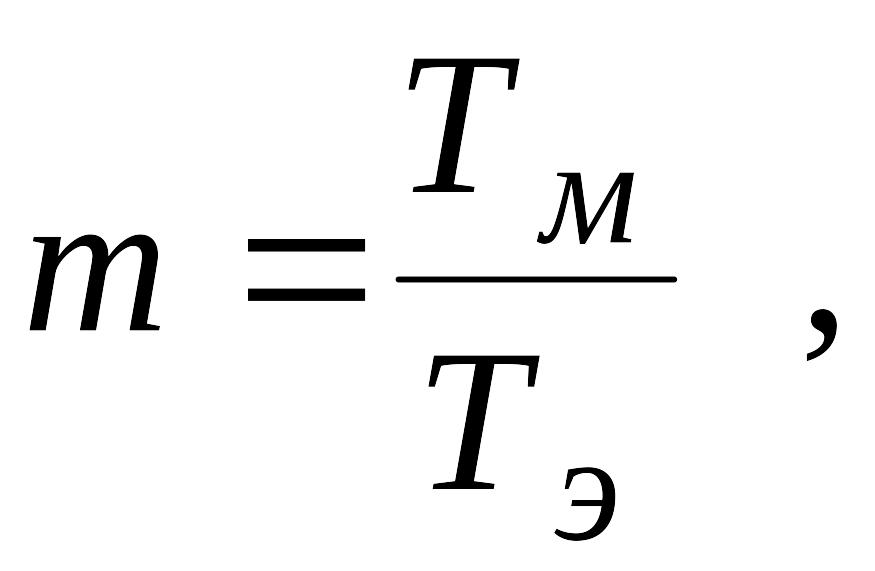
то
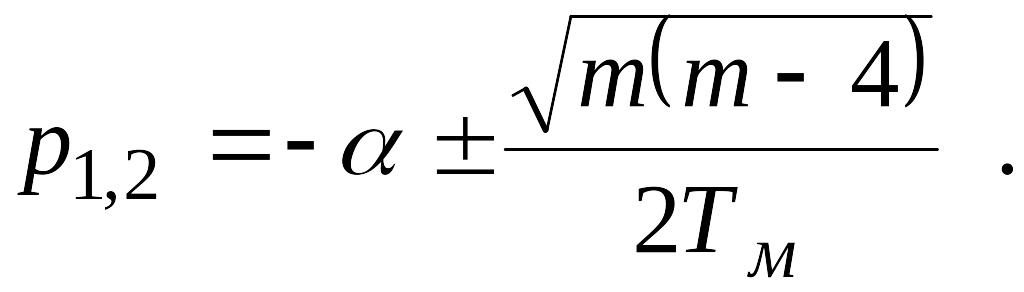
1)
m
<
4 –
комплексно-сопряженные корни:![]() р
резонансная (собственная) частота
колебаний электропривода,
р
резонансная (собственная) частота
колебаний электропривода,
коэффициент затухания;
2)
m
>
4 – два
разных отрицательных корня:![]()
минимальная частота собственных колебаний электропривода;
m = 4 – два одинаковых отрицательных корня:
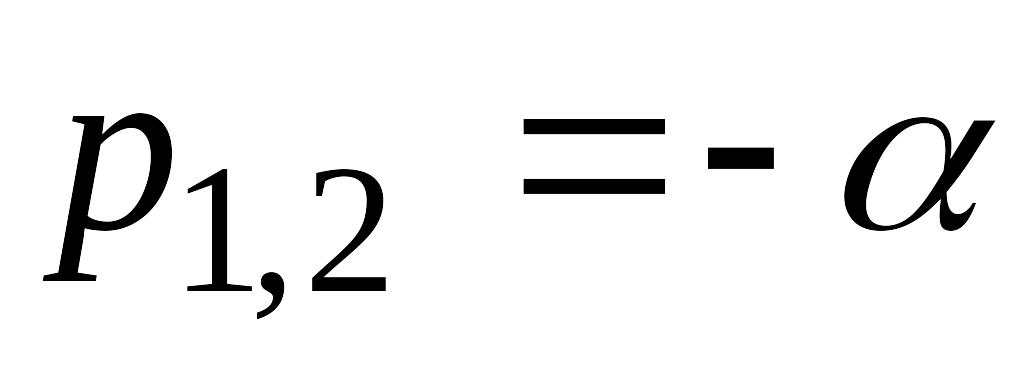 .
.
Очевидно, что уравнения (t) и М(t) для трех видов корней будут разными. Рассмотрим их. Для m < 4 можем записать решение дифференциального уравнения (1) в виде:а затем и уравнение угловой скорости электропривода в переходном процессе
![]()
Решение дифференциального уравнения (2) для электромагнитного момента
![]()
Если переходный процесс начинается с установившегося состояния, то уравнения могут быть преобразованы к виду:
![]()
![]() Где
Где![]()
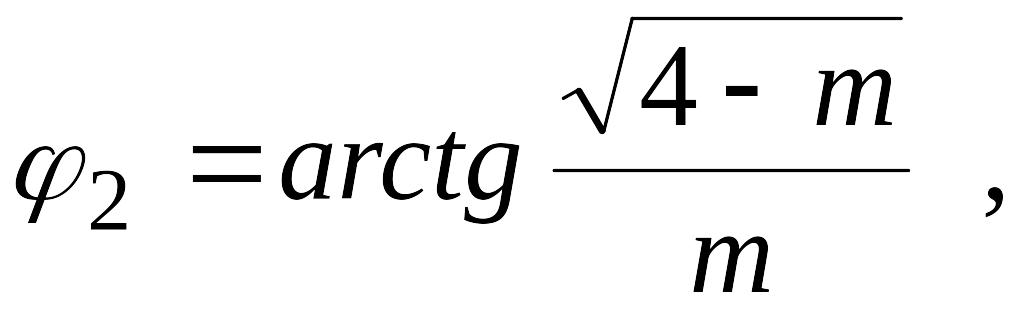 с.нач
, Мс.нач
– значения установившейся скорости и
момента двигателя перед началом
переходного процесса.
с.нач
, Мс.нач
– значения установившейся скорости и
момента двигателя перед началом
переходного процесса.
При m > 4 уравнение скорости и электромагнитного момента в переходном процессе будет искать в таком виде:
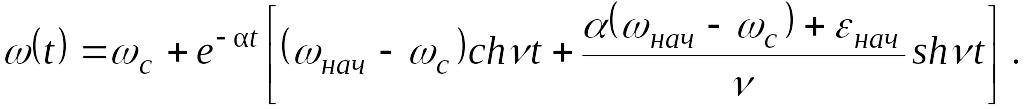
![]()
Если переходный процесс начинается с установившегося состояния, то можно преобразовать к такому виду:
![]()
![]() где
где![]()
![]()
В
случае кратных корней (m
=
4) решения
дифференциальных уравнений (1), (2) ищутся
в виде:![]()
![]()
где постоянные интегрирования А2 , В2 и С2 , D2 определяются из начальных условий
Использование этих начальных условий позволяет найти:
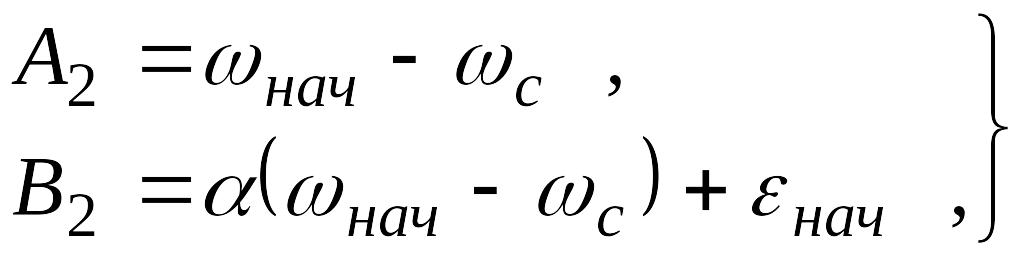
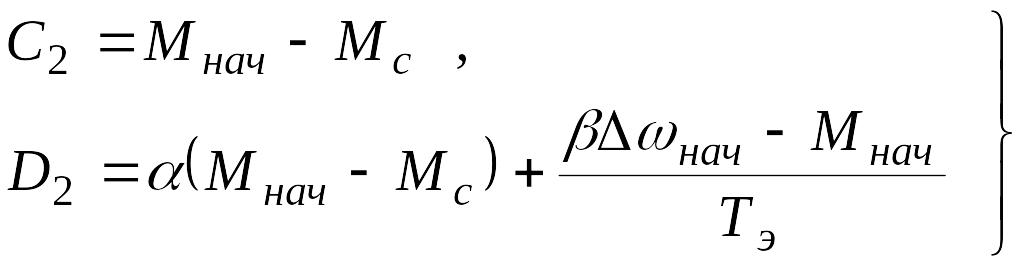
и окончательные уравнения скорости
![]()
и электромагнитного момента
![]()
Если переходный процесс начинается с установившегося состояния, то уравнения (могут быть представлены таким образом:
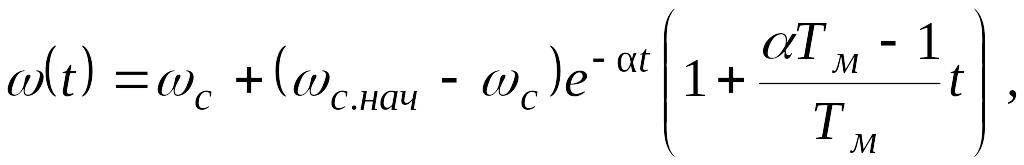
![]()
