Для трехфазной мостовой схемы выпрямления (8.90) / тогда (8.91)

С использованием эквивалентной схемы АД для цепи выпрямленного тока можно найти более точное значение сопротивления R_д :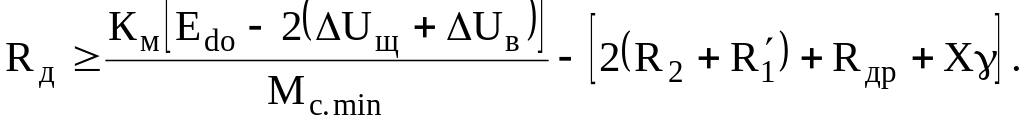 (8.92)

При постоянной величине выпрямленного тока ротора I_d на полупроводниковом ключе ПК в момент расшунтирования сопротивления R_д появляется напряжение (8.93)

которое может существенно превышать линейное номинальное напряжение ротора U_2ном. Оценим величину этого напряжения для номинального тока, обозначив

(8.94) номинальное сопротивление АД (8.95)

и активное сопротивление R_2,0 фазы ротора связаны соотношением

можем определить напряжение U_пк при номинальном токе в виде:

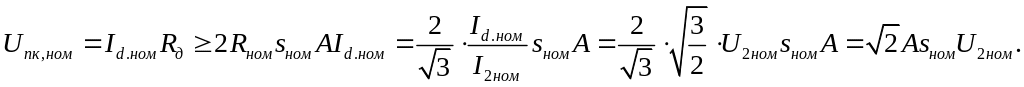
Из (8.97) находим превышение напряжения U_пк над номинальным напряжением ротора

(8.98)

Если взять М_с.min=0,2М_ном , то для крановых электродвигателей серии 4MTF(H) можно найти: а) для мощности 3,7 кВт: _u=8; U_пк=1520 В; б) для мощности 160 кВт: _u=6,5; U_пк=2650 В. Наличие импульсов напряжения выше 1000 В вносит свои особенности в эксплуатацию системы электропривода ИРС – АД.

Система ИРС – АД обеспечивает получение жестких механических характеристик в достаточно большом диапазоне скоростей. В этом состоит ее отличие от реостатного регулирования АД с дискретным изменением ступеней сопротивления. По энергетическим показателям и допустимому моменту она полностью соответствует ступенчатому реостатному регулированию. Потери мощности здесь даже несколько больше из-за пульсаций тока и наличия высших гармоник.

32 Закон костенко при частотном управлении идеализированного ад.

Скаляр переменного напряжения представляется только величиной , полученной с помощью непосредственного измерения , расчета или преобразования мгновенных значений . Следовательно , общей чертой всех скалярных систем управления является модуль регулируемой величины .Эта скалярная величина используется как в разомкнутых , так и в замкнутых системах частотного управления асинхронными двигателями .

Скалярное частотное управление берет свое начало с 1925 года , когда М.П.Костенко предложил свой закон частотного управления

для идеализированного АД, в котором:

1. активное сопротивление R₁ обмотки статора равно нулю ,

2. отсутствуют потери в стали ,

3. магнитная система ненасыщена ,

4. имеется независимое охлаждение .

Для идеализированного АД этот закон управления обеспечивает постоянство перегрузочной способности: (8.100)

и экономичное регулирование электрических машин,

где критический момент АД при текущей и номинальной частотах ,

статический момент при текущей угловой скорости двигателя и при номинальной скорости .

При этом

где s – скольжение ,

- число пар полюсов обмотки статора АД .

При использовании относительных безразмерных единиц :

(8.102)

закон М.П.Костенко записывается в виде :

Как показал А.А.Булгаков , закон частотного управления М.П.Костенко относится не только к частотному управлению , а вообще к любому управлению электродвигателем . В частности , при параметрическом управлении , когда

(8.104)

Если учесть , что в идеализированном двигателе = 0 , то

Следовательно , напряжение , подводимое к АД , надо изменять с изменением нагрузки. Этот принцип управления широко используется в современных асинхронных электроприводах для экономии электроэнергии , когда в цепь статора АД включаются полупроводниковые преобразователи напряжения , которые изменяют свое выходное напряжение (первую гармонику) пропорционально корню квадратному из относительного момента (тока) двигателя.