Вычисление предполагаемой стоимости

		Состояние	ЭКОНОМИКИ	Предполагаемая
Альтернативная стратегия	<р Л	N2 -25) (р = 0,	"з 50) (р = 0,25)	СТОИМОСТЬ E(S)
	20 40 10	10 10 10	20 0 10	15 15 10

В табл. 4.3 представлена матрица решения со следующими вероятностями: 0,25 для Л/,, 0,50 для N₂ и 0,25 для N_y Включена также величина отдач для трех различных стратегий, или проектов.

Предполагаемые стоимости вычисляются следующим образом:

ОД) = 0,25(20) + 0,50(10) + 0,25(20) = 15,0; E(S₂) = 0,25(40) + 0,50(10) + 0,25(0) = 15,0; Д5₃) = 0,25(10) + 0,50(10) + 0,25(10) = 10,0.

Понятно, что Sj или S₂ предпочтительнее S_y Но для того чтобы сделать выбор между S_i и S₂, имеющими одинаковую предполагаемую стоимость, мы должны использовать какой-то другой критерий. Таким критерием может оказаться степень риска. Посколь­ку предполагаемая стоимость служит измерением основной тенденции, степень риска может быть определена как степень отклонения возможных отдач от предполагаемой стоимости. Степень риска, таким образом, считается вторичным, или вспомогатель­ным, измерением предполагаемой стоимости.

Измерение риска: размах

и среднее квадратичное отклонение

Из табл. 4.3 следует, что хотя 5¹, и S₂ имеют одинаковую предполагаемую стоимость, равную 15, 'S_t фактически может иметь отдачу или в 20, или в 10, в то время как S₂ могла бы иметь отдачу или в 40, или в 10, или в 0. Интуитивно мы чувствуем, что чем дальше от среднего значения находится фактическая отдача, тем рискованнее будет проект. Следовательно, одним из способом измерения риска можно считать вычисление размаха, который представляет собой разность между самыми крайними величинами отдачи. В нашем примере размах S_t равен 10 (от низкого, равного 10, до высокого, равного 20), в то время как размах S₂ равен 40 (от низкого, равного 0, до высокого, равного 40).

Размах - это полезная предварительная оценка, но она учитывает лишь крайние стоимости и не учитывает стоимости, расположенные между ними. Если мы предпо­ложим наличие нормального распределения вероятности, то более точным измерени­ем риска будет статистика, называемая средним квадратичным отклонением (греческая буква «сигма»), которое является измерением отклонения отдачи от предполагаемой стоимости. Среднее квадратичное отклонение показывает жесткость распределения вероятности. Чем выше среднее квадратичное отклонение, тем выше вероятность воз­можной отдачи и, следовательно, тем выше риск.

91

Г лава 4. Выработка решения в условиях риска и неопределенности

В ычисление среднего квадратичного отклонения может производиться следующим образом.

Шаг 1. Вычислим предполагаемую стоимость (взвешенное среднее арифметичес­кое) распределения

ад=

(2)

где X. — i-я отдача, или результат; Р. - вероятность i-Pi отдачи;

Е(Х) — предполагаемая стоимость или взвешенный средний результат с вероят­ностями в качестве весов.

Шаг 2. Вычтем предполагаемую стоимость из каждого результата с целью получе­ния ряда отклонений от предполагаемой стоимости, т.е.

d, = X_t- E{X).

(3)

ШагЗ. Возведем в квадрат каждое отклонение, затем умножим возведенное в квад­рат отклонение на вероятность связанного с ним результата. Затем сложим результаты с целью получения среднего возведенного в квадрат отклонения, или дисперсии, о², распределения вероятности:

(4)

Шаг 4. Взяв корень квадратный из дисперсии, получим среднее квадратичное отклонение, а;

<■=!

(5)

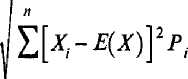
Уравнение (5) можно также записать в следующем виде:

поскольку среднее арифметическое распределение, ц_х (читается: «мю отЛ&), представ­ляет собой предполагаемую стоимость. Обозначения в уравнении (6) более понятные, чем в уравнении (5).

В табл. 4.4 продемонстрированы вычисления средних квадратичных отклонений для стратегий, представленных в табл. 4.3. Как следует из табл. 4.4, 5^ со средним квадратичным отклонением в 15 в три раза рискованнее, чем S_l со средним квад­ратичным отклонением в 5, в то время как $_г со средним квадратичным отклоне­нием, равным нулю, вообще не подразумевает риска.

92

		Выработка решения	s условиях	риска
Вычисление	среднего	квадратичного отклонения	Табли	ца 4.4
Стратегия (X. — [i)		- м)2 р, (X, - v

5 5	25 25 25	0,25 0,50 0,25	6,25 12,50 6,25
25 -15	625 25 225	0,25 0,50 0,25	О,2 = 25,00 156,25 12,50 56,25
0 0 0	0 0 0	0,25 0,50 0,25	О22 = 225,00 0,0 0,0 0,0
			аз2 = 0,0

= 5

Д ля любого нормального распределения кривая вероятности распределения сим­метрична относительно среднего. Зона под кривой представляет общую вероятность, равную 1,0, разделенную на две равные части. Таким образом, вероятность (зона) сле­ва от среднего равна 0,5 и вероятность справа ± 0,5. На рис. 4.1 проиллюстрирован этот принцип. Данный рисунок выполнен в стандартном масштабе, или в масштабе Z, который имеет среднее значение, равное нулю, и среднее квадратичное отклонение, равное ±1,0.

' 99,73% i

- За

-2а -1а

+2о +3а

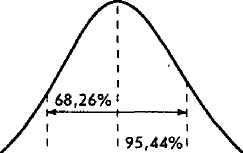
Рис. 4.1. Размах вероятности для нормального распределения

i

Если мы обратимся к таблице нормального распределения (см. табл. Е в Приложе­нии в конце данной книги), то увидим, что величина Z= 1,0 (означающая одно сред­нее квадратичное отклонение от среднего) соответствует размаху 0,3413. Следователь­но, размах между Z= -1,0 и Z- +1,0 равен 0,6826. Другими словами, если имеется вероятность, равная 68,26%, то фактический результат окажется в пределах одного среднего квадратичного отклонения от среднего (в любом направлении). При исполь­зовании той же самой процедуры размах в пределах ±2 средних квадратичных откло­нений от среднего равен 0,9544, или 95,44%, а размах в пределах ±3 средних квадра­тичных отклонений равен 99,73% (см. рис. 4.1).

Вернемся к нашим ранним сравнениям стратегий S_l и S_r На рис. 4.2 показано распределение вероятности для каждой стратегии, а также их среднее и среднее квад­ратичное отклонение. На этом рисунке размах в 68% вероятности (т.е. \у + 1а) показан как затененная область. Для распределения вероятности S_l это узкая полоса с разма-

93

Г лава 4. Выработка решения в' условиях риска и неопределенности

х ом от 10 до 20. Для распределения вероятности S₂ представлена более широкая полоса с размахом от 0 до 40, Понятно, что абсолютное отклонение возможных отдач гораздо выше для S₂, чем для S_v Более высокое отклонение говорит о том, что S₂ более риско­вая вероятность, чем £„ поскольку обе альтернативы имеют одинаковую предполага­емую стоимость.

s 0,10	-
1- u 1 °'°9 8- - 0,08	/
с 0,07	/ /
a 5 0,06
a 2 0,05 0 ™ 0,04 8- I 0,03 lo,O2 9	/		\		L
0,01					\		s ^Чч^^^
								* 1 i , , r 2

-20 -15 -10 -5

10 15 20 25

30 35 40 45 50 Стоимость отдачи

Рис. 4.2. Распределение вероятности двух стратегий с одинаковой предполагаемой стоимостью

Измерение относительного риска: коэффициент вариации

Предположим, что фирма имеет возможность осуществлять инвестиции в два раз­ных проекта. Один имеет предполагаемую стоимость в 500 000 долл. со средним квад­ратичным отклонением в 5000 долл. Другой имеет предполагаемую стоимость в 100 000 долл. со средним квадратичным отклонением в 2000 долл. Какой из них более рисковый?

Если мы воспользуемся средним квадратичным отклонением для измерения риска, то мы должны будем сделать вывод, что более крупный проект является более риско­вым. Но если учитывать среднее квадратичное отклонение в отношении размера про­екта, то относительный риск будет ниже для более крупного проекта. Понятно, что для того чтобы сравнивать рисковость проектов с сильно отличающимися величинами инвестиций, отдач и предполагаемой стоимости, необходимо пользоваться скорее от­носительными, чем абсолютными измерениями. Относительное среднее квадратичное отклонение (чаще называемое коэффициентом вариации) и является таким измере­нием.

94

_т

Выработка решения в условиях риска

К оэффициент вариации — это отношение среднего квадратичного отклонения к предполагаемой стоимости, или среднему. Вычисленный в процентах, он является ин­дексом риска в расчете на доллар прибыли и, таким образом, обеспечивает возмож­ность сравнения относительного риска стратегий или проектов с сильно различаю­щейся величиной. Формула имеет вид:

О—(100),

(7)

где а — среднее квадратичное отклонение;

ц — предполагаемая стоимость (средняя величина).

Базируясь на данных, представленных в табл. 4.3 и 4.4, рассчитаем коэффициенты вариации для каждой стратегии:

для 5¹,: С,

для S₂:

-jjJ(lOO) = 33; = 100;

для Д₃: С₃ -

В данном случае использование коэффициента вариации приводит к тем же самым выводам, которые были достигнуты, когда среднее квадратичное отклонение было использовано для измерения риска. Но этого может не произойти, если предполагае­мые стоимости будут другими. Например, предположим, что мы выполняем два про­екта и что имеют место три возможных состояния экономики: N_v N₂ и N₃ с вероятно­стями в 0,20, 0,70 и 0,10 соответственно. В табл. 4.5 рассматриваются два проекта - S_A и 5₅, их предполагаемая отдача, предполагаемая стоимость, E(S), среднее квадратич­ное отклонение, a_sn и коэффициент вариации, С\, для каждого проекта.

Таблица 4.5

				Анализ	риска для двух	проектов
Проект	(Р	= 6,20)	(Р	- 6,70)	(Р = 6,10)		°«		csi
		20 150		10 100	5 75	11,5 107,5	4, 22,	5 5	39 21

Мы видим, что S_s наверняка представляет собой намного более крупный проект, чем S₄, с более высокой предполагаемой стоимостью, для которой имеет место более высокое среднее квадратичное отклонение. Более высокое среднее квадратичное от­клонение означает более высокий абсолютный риск. Но относительный риск (т.е. риск в расчете на доллар предполагаемой стоимости, измеряемый коэффициентом вариа­ции), грубо говоря, вполовину выше для S_p чем для 5₄. Поскольку предполагаемая стоимость S_s также выше, чем предполагаемая стоимость S_A, мы можем сделать вывод, что S_s является более желательным проектом.

Компромисс между риском и прибылью

Какую стратегию выберет лицо, принимающее решение, зависит от его отношения к риску в связи с отдачей, а также от других соображений, таких, как общее финансо­вое положение этого лица. На рис. 4.3 рассматриваются предполагаемая прибыль и

95

_Г

Главв 4. Выработка решения в условиях риска и неопределенности

о тносительный риск для 5,, S₂, 5₃, а также стратегий или проектов, проанализирован­ных ранее в табл. 4.3.

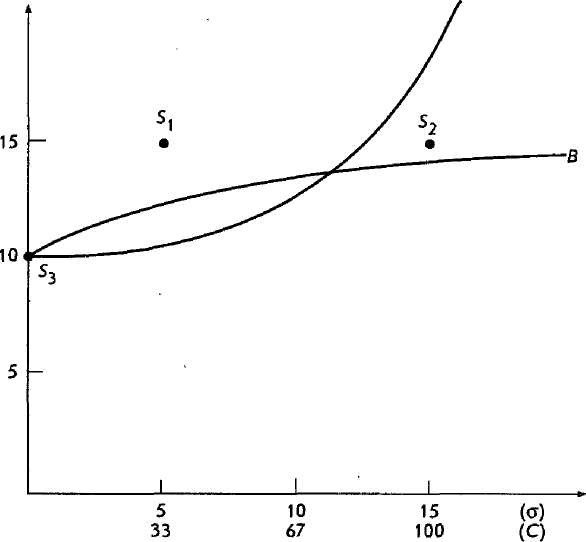
Ось абсцисс на рис. 4.3 представляет абсолютный риск (который измеряется сред­ним квадратичным отклонением, о) и относительный риск (который измеряется ко­эффициентом вариации, С). Ось ординат представляет среднюю прибыль стратегии или проекта в долларах. Пересечения прибыли и риска для трех стратегий - это точки S_lt S₂ и Sy

I

а

Абсолютный риск (а) и относительный риск (С)

Рис. 4.3. Диаграмма риска—прибылей

Кривые Aw В представляют функции риска—прибылей лица, принимающего реше­ние А и решение В соответственно. Эти кривые представляют требуемую прибыль как функцию риска (они называются также кривыми рыночного безразлнчия). Кривая А отражает неприятие риска, поскольку по мере того, как риск возрастает, требуемая прибыль возрастает увеличивающимися темпами. Кривая В отражает отношение лица, подвергающегося риску, По мере повышения риска требуемая прибыль также увели­чивается, но не так быстро.

Желательность предполагаемой прибыли измеряется ее удаленностью от вертикаль­ной оси и расположением относительно кривой компромисса лица, принимающего решение риска—прибыли. Лицо, принимающее решение А, может не рассматривать стратегию S_v потому что она находится ниже его кривой. Он,может выбрать S_v пред­почтя ее 5₃, если даже S₃ и будет свободна от риска, потому что предполагаемая при­быль S_{ выше, чем прибыль, которая ему требуется после должного учета риска. Лицо, принимающее решение В, может рассмотреть все три стратегии, которые можно счи­тать приемлемыми, но оно также должно выбрать S_it потому что она обещает самую высокую прибыль.

96

4—1854

В ыработка решения в условиях риска

П олезность, страх риска и премия за риск

В обширном море человеческих личностей, без сомнения, есть люди, которые идут на риск, и люди, которые безразличны к нему. Но и здравый смысл, и эмпирические наблюдения говорят о том, что большинство инвесторов и руководителей бизнеса стре­мятся избегать риска. Почему? Множество теорий пытаются объяснить этот факт по­ведения человека, но наиболее удовлетворительным объяснением можно считать тео­рию полезности.

Полезность и принятие решения. Предположим, что две строительные фирмы при­глашены принять участие в конкурсе на лучшую проектную спецификацию для круп­ного строительства. Компания А с активами в сумме 50 млн долл. значительно круп­нее, чем компания В, активы которой составляют всего лишь 10 млн долл. Однако стоимость подготовки предложения (1 млн долл.) одинакова для обеих компаний, причем она не будет возмещена фирме, предложение которой не будет принято. Ком­пания, которая выигрывает конкурс, может рассчитывать на прибыль в 25 млн долл. при выполнении строительных работ.

Руководство обеих компаний считает, что они имеют равные шансы на победу в конкурсе¹. Альтернативы следующие: выиграть или не выиграть. Если выигрывают обе компании, то предполагаемая стоимость для каждой (в млн долл.) составляет:

Е (прибыль) = 0,5(-1) + 0,5(25) = 12.

Несмотря на тот факт, что предполагаемая стоимость участия в конкурсе составля­ет 12 млн долл., фирма меньшего размера может предпочесть не принимать в нем участия. Почему?

Причина в том, что 12 млн долл. — это лишь теоретическая средняя прибыль, под­считанная на базе многих экспериментов. Однако в реальной жизни имеет место лишь один эксперимент, в котором компания или выигрывает 25 млн долл., или теряет 1 млн долл. Если такая потеря приводит фирму к банкротству, то она не должна рис­ковать своим выживанием, независимо от того, насколько велики потенциальные выгоды. С другой стороны, если компания способна перенести убытки в сумме 1 млн долл., то она может пойти на риск.

Вывод, который можно сделать, состоит в том, что преобразование долларовой отдачи в какую-то другую структуру вознаграждения может оказаться необходимым до того, как можно будет провести соответствующий анализ. Если долларовая сто­имость не отражает адекватно чувств лица, принимающего решение, или его отно­шения к прибылям или убыткам, то она должна быть преобразована в более понят­ное измерение.

Полезность как раз и является таким измерением, и она может быть выражена в концептуальных единицах, называемых утилямн². К сожалению, никто не имеет воз­можности установить стандартный утиль, которым можно было бы производить коли­чественные измерения полезности. Тем не менее это понятие полезно. Менеджеры, принимающие решение интуитивно, используют это понятие, когда они определяют порядок предпочтения альтернатив: т.е. самый высокий уровень полезности ставится первым, следующий уровень идет вторым и т.д. Таким образом, очень практичное

¹ Если обе фирмы уже вступали в аналогичное соревнование в прошлом, то уверенность руководства могла бы базироваться на опыте. В этом случае оно применяет объективные веро­ ятности в условиях риска. Но еспи руководство не имеет эмпирических данных, на основе кото­ рых у него могло бы сложиться свое мнение, то примененные вероятности будут субъективны­ ми оценками, сформированными в условиях неопределенности (в данном случае в соответствии с Бэйесовым постулатом о равных вероятностях).

² От ангп. utility {полезность, выгодность). — Примеч. ред.

97

4-1854

Г лава 4. Выработка решения в условиях риска и неопределенности

п орядковое измерение полезности базируется на количественном измерении, даже если оно фактически и невозможно.

Риск и убывающая предельная полезность. Здесь необходимо пояснить формаль­ную зависимость между риском и полезностью. Для этого прибыли и убытки должны быть измерены с точки зрения предельной полезности, а не с точки зрения абсолют­ной стоимости в долларах. Предельная полезность определяется как изменение общей полезности, которое происходит тогда, когда еще одна денежная единица прибывает или убывает. В предыдущем примере, если компания не сможет нести убытки в разме­ре 1 млн долл., то она назначит более высокую предельную полезность потерянным долларам, а не долларам, которые могут быть приобретены.

Три способа, посредством которых полезность может быть теоретически связана с доходом, представлены на рис. 4.4 a, b, с.

Утипи

Утмли

Утили

37 л 34

«25 о

12 3 4 5 Доход ($000)

_I

с о

		в1	в
	1			/
	1			/
	1			/
	1
	1			/
	1
/ /
/	/
	•

1 2 3 Доход ($000)

|2

и О

о

1 2 3 Доход ($000)

Рис. 4.4. Полезность дохода

На этих трех вариантах рисунка рассматривается поведение различных типов инвесторов при увеличении дохода от инвестиций равными приращениями. Оси абсцисс представляют доход, измеряемый в долларах; оси ординат — полезность приобретенных долларов, измеренную в утилях. Каждая кривая представляет по­лезность как функцию дохода; наклон каждой кривой — предельную полезность.

Обычный инвестор (рис. 4.4, а) старается избегать риска. Причина стремления из­бегать риска выражена убывающей предельной полезностью. Этот рисунок показывает, что при отсутствии инвестиций отсутствуют и прибыли. После получения первой 1000 долл. общая полезность возрастает на 16 утилей по мере того, как инвестор удовлетво­ряет срочные нужды. Вторая 1000 долл., хотя, без сомнения, и желательна, необходима не так остро, как первая. Следовательно, общая полезность возрастает всего только на 9 утилей. Таким образом, предельная полезность для второй 1000 долл. составляет 9 утилей, если сравнивать с 16 утилями для первой 1000 долл. Когда получена третья 1000 долл., общая полезность возрастает до 30 утилей, но предельная полезность па­дает до 5 утилей. Понятно, что предельная полезность убывает по мере увеличения прибыли или дохода. Это основной фактор риска, и он оказывает решающее воздей­ствие на поведение инвестора.

Например, предположим, что инвестор может делать выбор между свободными от риска инвестициями в государственные облигации, которые могут обеспечить доход в 30 000 долл., и инвестициями в акции новой электронной фирмы, которая может обес-

98

Выработка решения в условиях риска

п ечить доход в 40 000 долл., если все пойдет хорошо, но только в 10 000 долл., если ее дела пойдут не так хорошо, как ожидалось. Предположим также, что тщательное ис­следование убеждает инвестора в следующем: вероятность того, что новая продукция пойдет хорошо, составляет 0,75. Предполагаемая долларовая стоимость обоих проек­тов следующая:

Е (государственные облигации) = (1,0) ($30 000) = $30 000;

Е (новое предприятие) = 0,75 ($40 000) + 0,25 ($10 000) = $32 500.

Предполагаемые стоимости полезности (в утилях) обоих проектов (см. рис. 4.4 а) равны:

Е (государственные облигации) = (1,0) (30) = 30; Е (новое предприятие) - (0,75) (34) + (0,25) (16) = 29,5.

Таким образом, мы видим, что предполагаемый денежный доход выше у новой элек­тронной фирмы, но предполагаемая полезность выше у свободных от риска государ­ственных облигаций. Следовательно, инвестор, старающийся избегать риска, предпо­чтет купить государственные облигации.

Прямые линии на рис. 4.4 Ъ имеют постоянные наклоны, характеризующие чело­века как безразличного к риску, для которого предельная полезность потерянного дол­лара равна предельной полезности полученного. Безразличие к риску — это, однако, не то же самое, что безразличие к прибылям. Человек, представленный в части В\ назначает более высокую стоимость полезности полученного или потерянного долла­ра, чем это делает человек, представленный в части Д а человек, представленный в части В, получает более высокую полезность от доллара по сравнению с человеком, представленным в части В".

На рис. 4.4 с предельная полезность становится более высокой по мере увеличения дохода. Это отражает случай с заядлым игроком, который придает более высокую полезность полученным долларам, а не потерянным. Поднимающаяся вверх кривая, таким образом, описывает поведение тех, кто готов принимать на себя риск — чем больше они выигрывают, тем более важной становится победа.

Понятно, что поведение человека может соответствовать одной из кривых, пред­ставленных на рис. 4.4 а, Ь, с, или даже какой-то совершенно иной кривой. Может оказаться несколько заядлых игроков (этот тип представлен на рис. 4.4 с), которые фактически добиваются успеха в деле. Может оказаться также несколько руководите­лей, которые проявляют безразличие к риску (этот тип представлен на рис. 4.4 Ь), потому что они не сознают его или не понимают его значения. Если такие руководи­тели и существуют, то они, конечно, в меньшинстве. Большинство руководителей принадлежат к типу, представленному на рис. 4.4 а, т.е. они остро чувствуют риск предпринимательства. Они больше страдают от потери доллара, чем радуются его приобретению. Следовательно, функция полезности большинства руководителей биз­неса демонстрирует убывающую предельную полезность. Действительно, подобное по­ведение преобладает в такой степени, что допущение убывающей предельной полез­ности служит одним из двух краеугольных камней экономической теории¹.

Премии за риск. Неприятие риска со стороны инвесторов и руководителей демон­стрируется многими различными способами. Предположим, что облигации класса АА продаются по более высокой цене, чем облигации класса В. Инвесторы осуществляют диверсификацию или посредством создания индивидуальных портфелей, или путем осуществления инвестиций в совместные фонды. Люди вкладывают свои деньги на сберегательные счета с низкими процентными ставками, но страхуемые федеральным правительством, более охотно, чем в облигации, обеспечивающие намного более вы-

¹ Другим краеугольным камнем является закон убывающей предельной прибыли, примени­мый к вводимым факторам производства (см. гл. 10).

99

Г лава 4. Выработка решения в условиях риска и неопределенности *

с окий процент. Кроме того, они покупают всевозможные страховки на случай несчас­тного случая или смерти.

Почему же тогда, раз инвесторы стремятся избегать риска, они все-таки вкладыва­ют свои деньги в обыкновенные акции, в товары, драгоценные металлы, в коллекции и другие рисковые инвестиции? Ответ заключается в том, что они не сделают этого, если не будут получать премию за риск. Инвестор хочет иметь компенсацию не только за использование своих денег, но также и за риск их потери. Другими словами, инве­стор требует более высокой нормы прибыли, если присутствует риск.

Для иллюстрации понятия «премия за риск» предположим, что женщина имеет функ­цию полезности, аналогичную функции, представленной на рис. 4.5, и что ее просят за­ключить пари на 1000 долл. на подбрасывание монеты с равными шансами; т.е. вероят­ность выигрыша составляет 0,5 и вероятность проигрыша тоже равна этому числу.

Функция полезности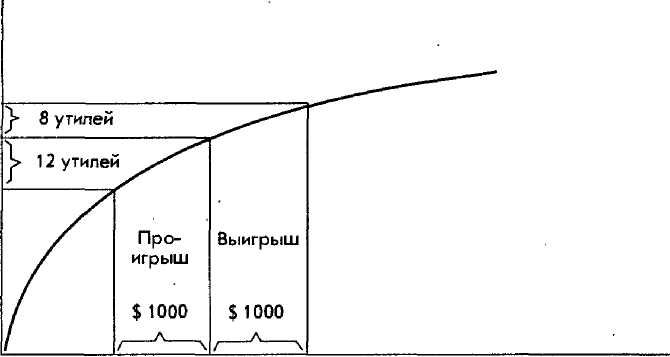

|2 и о

X

п

_I

Доход

Рис. 4.5. Полезность пари без премии за риск

Таким образом, если она выиграет, то получит 1000 долл., а если проиграет, то запла­тит 1000 долл. Должна ли она заключать пари? Чтобы получить ответ, давайте еще раз обратимся к рис. 4.5, на котором представлены инвестиции без премии за риск.

Если инвестор выигрывает 1000 долл., то он получает 8 утилей полезности; но если он проигрывает, то он жертвует 12 утилями. Поскольку вероятность выигрыша или проигры­ша одинакова, предполагаемая стоимость в утилях составляет 0,5(8) + 0,5<—12) = -2. По­скольку предполагаемая стоимость отрицательна, понятно, что инвестор не должен заключать пари.

Теперь давайте предположим, что тот же инвестор получит премию, если он заклю­чит пари. Если женщина проиграет, то она потеряет 1000 долл., но если она выиграет, то она получит 1800 долл. И опять шансы составляют 50 : 50. Должна ли она заключать пари? Давайте обратимся к рис. 4.6.

И опять ответ зависит от функции полезности инвестора. Как показывает кривая, представленная на рис. 4.6, потери в сумме 1000 долл. принесут потери полезности в размере 12 утилей, в то время как выигрыш в 1800 долл. принесет увеличение полез­ности на 12 утилей. Предполагаемая стоимость пари в таком случае будет равна 0,5<—12) + 0,5(+12) = 0, что означает, что инвестор может быть безразличным к пари; т.е. что женщина может и согласиться на пари, а возможно, и отказаться от него. Если премия за риск будет увеличена, то она согласится на пари; но если премия за риск будет уменьшена, то она наверняка откажется.

100

Выработка решения в условиях риска

Функция полезности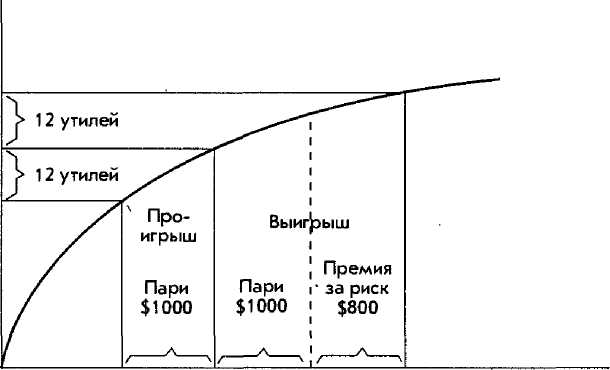

_е

о 5

Доход

Рис. 4.6. Полезность пари с премией за риск

Теперь давайте предположим, что тому же самому инвестору предлагается еще одно пари на 500 долл., опять с подбрасыванием монеты. Потребует ли она вновь премию в 800 долл. на пари в сумме 500 долл.? На этот раз обратимся к рис. 4.7, из которого следует, что потеря 500 долл. для этого инвестора означает потерю 5 утилей. Для того чтобы выиграть 5 утилей, инвестору требуется премия за риск в сумме 100 долл. Но эти 100 долл. — лишь ¹/& премии за риск в 800 долл., требуемой за пари на сумму в 1000 долл. Можно сказать, что если сумма пари удваивается, то требуемая премия за риск возрастает в 8 раз. Как это возможно?

л I-и

о

z «

, 5 утипей			■ Функция
у . ^-				полезности
		Вы­игрыш $600 ,—Л
\ ^* 5 утипей ^*г	Про­игрыш $500

Доход

Рис. 4.7. Премия за риск для меньшего пари

Ответ, конечно, заключается в форме функции полезности, или кривой инвестора. Риск измеряется дисперсией возможных результатов. Поскольку дисперсия в +1000 долл. вдвое выше, чем дисперсия в +.500 долл., вполне возможно, что риск должен быть вдвое большим. Но на рис. 4.6 и 4.7 мы видим, что если премия за риск добавляется к выигравшей стороне пари, то дисперсия возможных результатов меняется, следова­тельно, риск тоже меняется.

101

Г лава 4. Выработка решения в условиях риска и неопределенности

Д ва широко известных ученых - Милтон Фридмен и Леонард Дж. Сэйвидж — были обеспокоены традиционным подходом, основанным на предельной полезности, о ко­тором мы говорили, потому что он не объясняет, почему человек может одновременно демонстрировать поведение принятия на себя риска и стремление избежать риска. Например, человек, который играет (первый тип поведения), с большей вероятностью поедет в казино на застрахованном автомобиле и будет жить в застрахованном доме (второй тип поведения). Фридмен и Сэйвидж пытались объяснить такое поведение гипотезами функции полезности, которая вначале растет, а затем стабилизируется и падает (рис. 4.8)¹.

| О

Доход Рис. 4.8. Функция полезности Фридмена—Сэйвиджа

Отношение инвестора к риску зависит прежде всего от формы кривой полезности, которая, в свою очередь, зависит от личности инвестора, а затем — от текущего поло­жения каждой кривой, которое определяется текущим доходом. Если текущий доход низок, то предельная полезность дохода (измеряемая наклоном кривой) высока, и че­ловек готов согласиться на риск при более низкой премии, чем в том случае, когда доход высок. Или, как утверждает гипотеза Фридмена—Сэйвиджа, на низких уровнях дохода человек может даже искать риск.

Деловой риск и финансовый риск. Для фирмы премия за риск имеет два компонен­та: деловой риск и финансовый риск. Деловой риск связан с решениями фирмы по по­воду инвестиций. Он определяется как относительная дисперсия от чистого операци­онного дохода фирмы и может измеряться коэффициентом вариации.

Деловой риск в некоторой степени всегда присутствует, потому что ни один бизнес не гарантирует успеха. Степень риска зависит от характера предпринима­тельской деятельности и от демонстрируемых навыков управления. Некоторые виды предпринимательской деятельности по своей природе более рисковые, чем другие. В пределах одного вида этой деятельности инвестор обычно сталкивается с более высоким деловым риском во вновь созданной фирме,.а не в фирме, давно успешно функционирующей. С другой стороны, «старая» фирма, продукция или методы пред-

' См. Milton Friedman and Leonard J. Savage, «The Utiliiy Analysis of Choices Involving Risk», Journal of Political Economy, August 1948, pp. 279-304.

102

Выработка решения в условиях риска

п ринимательства которой устарели, может иметь достаточно высокую степень дело­вого риска.

Финансовый риск отличается от делового риска. Если деловой риск определяется решениями фирмы по поводу инвестиций, то финансовый риск определяется фи­нансовыми решениями фирмы. Финансовый риск характеризуется двумя аспекта­ми: 1) риском возможной неплатежеспособности и 2) изменчивостью доходов, доступ­ных обычному акционеру.

Если фирма включает долгосрочную задолженность в структуру своего капитала, то финансовый риск должен быть добавлен к деловому риску с целью определения обще­го риска, перед лицом которого стоит фирма. Это происходит потому, что доходы должны идти прежде всего на оплату обслуживания задолженности (выплаты в основ­ной капитал и погашение процентов). Чем выше задолженность, тем выше вероят­ность тото, что наличных доходов может оказаться недостаточно для ее обслуживания. Если фирма не способна осуществить требуемые платежи, то она будет вынуждена признать себя банкротом. В меньшей степени риск вызывается также продажей льгот­ных акций, потому что дивиденды на льготные акции должны выплачиваться после обслуживания задолженности, но до того, как инвесторы в акционерный капитал могут получить какую-либо прибыль на свои инвестиции.

В любом случае, чем больше фирмы должны выплачивать из своих доходов на об­служивание задолженности, тем меньше средств остается для распределения между акционерами. Если распределение вероятности может быть определено для доходов акционеров, то финансовый риск также может быть измерен коэффициентом вариа­ции.

Корректировка риска

При оценке отдачи для конкретной стратегии лицо, принимающее решение, долж­но учитывать и текущую стоимость будущих прибылей, и степень риска. Оба эти ас­пекта объединены в следующей модели оценки:

R.

"/п

(8)

где NPV_[ — чистая текущая стоимость денежного потока наличности, связанного с ин­вестициями;

1,2,

R.

предполагаемая прибыль (поток наличности за период / для t после выплаты всех расходов за период);

требуемая норма прибыли, учитывающая уровень делового и финансово­го риска;

количество учитываемых периодов;

Л_Л ~"~

сумма начальных инвестиций, представляющая собой отток ^наличности (отрицательное число) при t — 0.

Несколько способов учета риска в модели оценки обсуждаются в финансовых пуб­ликациях. Двумя наиболее часто применяемыми методами являются следующие: ме­тод учетной ставки, скорректированной с учетом риска, и метод эквивалента определен­ности.

■ Учетная ставка, скорректированная с учетом риска. Мы можем определить учетную ставку, скорректированную, с учетом риска, как необходимую норму прибыли от пред­полагаемых инвестиций после должного учета имеющегося риска. Как уже говорилось ранее, каждая фирма имеет представление о необходимой норме прибыли, отражаю­щей ее восприятие нормального риска (нормальный деловой риск плюс финансовый

103

Г лава 4. Выработка решения в условиях риска и неопределенности

р иск). Если уровень риска предложенного проекта или инвестиций кажется не превы­шающим нормальный риск фирмы, то величина г в уравнении (8) будет представлять собой нормальную требуемую норму прибыли. Но если допускаемый или предполага­емый предложением риск выше нормального уровня риска фирмы, то более высокое значение г будет использовано в уравнении (8) для компенсации его более высокого уровня.

Например, предположим, что нормальный деловой и финансовый риск фирмы тре­ бует 20%-ной нормы прибыли. Фирма рассматривает стратегию инвестиций, которая первоначально стоит 100 000 долл. и обещает обеспечивать 50 000 долл. притока на­ личных средств в год в течение следующих трех лет. ' .

При ставке дисконтирования в 20% чистая текущая стоимость инвестиций и при­были на них определяются следующим образом:

$50000

( 1,20) (1,20)

$50000

Чистая текущая стоимость является положительной, следовательно, проект прием­лем. Он обещает обеспечивать чистую текущую стоимость в 20% прибыли на инвести­ции плюс 5324 долл. Но предположим, что существующий уровень риска, по мнению управляющих, должен обеспечивать 25% прибыли. Тогда чистая текущая стоимость должна быть выражена следующим образом:

$50000

( 1,25) (1,25)² (1,25)³

Теперь чистая текущая стоимость отрицательна. Предложение не будет обеспечи­вать учетную ставку в 25% прибыли из-за дефицита в 2400 долл., и оно должно быть отвергнуто.

Таким образом, мы видим, что при методе учетной ставки, скорректированной с учетом риска, который применяется для оценки предполагаемых инвестиций, риск в полной мере отражается ставкой дисконтирования и процессом дисконтирования. Од­нако имеют место по крайней мере три ограничения для такого подхода.

11. Как мы определяем соответствующую учетную ставку? Понятно, что внедрение новой продукции — более рискованное мероприятие, чем покупка государствен­ ных облигаций, но в какой степени? Очень трудно решить этот вопрос последова­ тельно и объективно, особенно если не имеется исторического опыта и ретроспек­ тивной информации, на основе которых можно делать оценку.

12. Этот метод не учитывает распределение вероятности будущего потока налично­ сти — информацию, которая могла бы иметь большую ценность.

13. Учетная ставка, скорректированная с учетом риска, не предлагает какого-либо по­ следовательного метода оценки риска, оценки, которая может быть полностью субъ­ ективной. Такое ограничение может быть преодолено с помощью метода эквива­ лента определенности.

Метод эквивалента определенности. Метод учетной ставки, скорректированной с учетом риска, учитывает риск просто путем модифицирования учетной ставки, г, в знаменателе модели оценки. И напротив, метод эквивалента определенности учитыва­ет риск в числителе модели оценки и применяет учетную ставку, свободную от риска, i (такую, как норма прибыли на государственные облигации), в знаменателе с целью учета стоимости денег в зависимости от временного периода. Степень риска отражена в числителе посредством умножения предполагаемой прибыли в связи с риском, R_p на коэффициент эквивалента определенности, а, с целью получения свободной от риска эквивалентной величины, R*, т.е.

104

Выработка решения в условиях риска

( 9)

отсюда

V

Уравнение (10) говорит о том, что

_ Предполагаемая эквивалентом прибыль без учета риска в t-й период Предполагаемая прибыль с учетом риска в Г-й период

Это меняет модель оценки на

(10)

_S

et,Л / ч, ■'о ( )'

(И)

R

г де NPVj — чистая текущая стоимость денежного потока, связанного с инвестици­ями;

• R.

  i п

  коэффициент эквивалента определенности для t-vo периода;

• предполагаемый поток наличных средств в период /, подверженный риску;

• свободная от риска эквивалентная величина наличных средств в период ?,

• свободная от риска норма прибыли или процентная ставка;

• количество рассмотренных периодов;

/₀ — сумма начальных инвестиций, представляющая собой отток наличных де­нежных средств (отрицательное число) при t — 0,

Коэффициент эквивалента определенности, а, — это число между 0 и 1, которое отражает функцию риска лица, принимающего решение. Он изменяется обратно про­порционально степени риска, т.е. чем выше риск, тем меньше должен быть коэффи­циент. Величина, равная 0, означает, что лицо, принимающее решение, считает проект слишком рискованным для того, чтобы от него можно было ожидать реальной прибы­ли. Величина, равная 1, означает, что лицо, принимающее решение, считает проект свободным от риска. Таким образом, а и связанное с ним R* служат базой для оценки риска лица, принимающего решение.

Предположим, что мы имеем фирму, рассматривающую возможность осуществить инвестиции в сумме 100 000 долл., которые способны обеспечивать приток наличных средств (в ситуации риска) в сумме 50 000 долл. в год на протяжении трех лет. Пред­положим также, что восприятие риска руководством фирмы таково, что оно считает получение свободных от риска 45 000 долл. в первый год, 40 000 долл. во второй год и 35 000 долл. в третий год эквивалентным получению подверженной риску прибыли в сумме 50 000 долл. каждый год. Тогда коэффициент эквивалента определенности должен иметь следующий вид;

а, =

¹ $50 000

$40 000 $50 000

$35 000 $50 000

= 0,90 или 90%; = 0,80 или 80%; = 0,70 или 70%.

105