Вопрос 38. Теорема о существовании первообразной для непрерывной функции. Формула Ньютона – Лейбница.

Теорема о существовании первообразной непрерывной функции

Если f(x) непрерывна на [a,b] , то она имеет там первообразную , которую можно представить в виде :

Ф(x) = ,где X₀- точка из [a,b]

Доказательство

Если X₀=a

Пусть X₀>a , тогда при x>X₀следует применить теорему о дифференцируемости определенного интеграла к отрезку [a,b]

Пусть x<X₀

Формула Ньютона- Лейбница.

Если f(x) непрерывна на [a,b] и F(x) – некоторая её первообразная , то

Докозательство.

Известно , что Ф(x) = - первообразная , она может отличаться от F(x) не более чем на константу.

В этой формуле берем сначала x=a , потом x=b.

0=F(a)+C

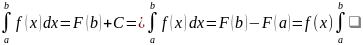
Вопрос 39. Замена переменной и интегрирование по частям в определенном интеграле.

Интегрирование по частям

Пусть U(x) и V(x) непрерывно дифференцируема на [a,b] , т.е U’(x) и V’(x) непрерывны. (U(x)V(x))’=U’(x)V(x)+U(x)V’(x) интегрируемы на [a,b]. . Слева интеграл равен U(x)V(x). Окончательно получаем 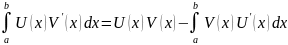или кратко:

Пример от руки!

Замена переменных

Пусть дан и f(x) непрерывна на [a,b]. Пусть функция x= удовлетворяет условию:

1) : a=

2) непрерывны на [

3) f[ также непрерывна на [

Тогда

Доказательство . Пусть F(x) – некоторая первообразная f(x) тогда F(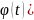 - первообразная функции а(