Вопрос 9. Первый замечательный предел и его следствия.

Следствия:

=1

Пусть α(x) – б.м. в точке Х₀ R , причем α(х) не равно 0 в некоторой окрестности точки, тогда =1

Доказывается по теореме о сложной функции.

Вопрос 11. Сравнение предельного поведения функции. Сравнение бесконечно малых функций. Свойства эквивалентных функций. Примеры.

Сравнение предельного поведения функций

f₁ = x²

f₂ = x⁴

x->0

Пусть даны f₁(х) и f₂(х) в некоторой окрестности точки Х0, ричем f₂(х) не равно нулю.

Определение 1 .

Функции f₁(х) и f₂(х) называются эквивалентными в Х0 , если =1

Определение 2.

f₁(х)= О* (f₂(х)) , О – большое, если = k , k не равно нулю.

Определение 3.

f₁(х) = о*(f₂(х)), о- малое, если = 0

Примеры от руки :

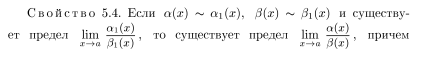
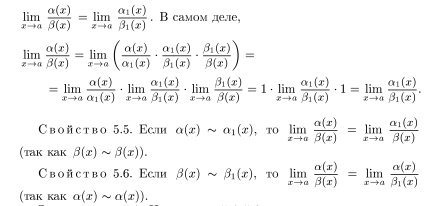
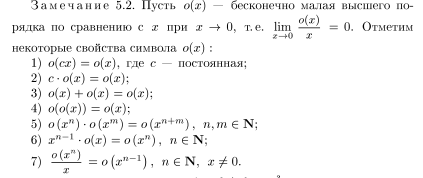
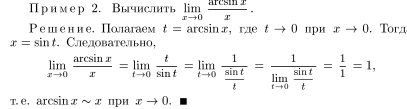
Вопрос 13. Теорема об обращении непрерывной функции в ноль . Теорема о промежуточном значении непрерывной функции.

Теорема об обращении непрерывной функции в ноль

Если f(x) непрерывна на [a,b]и на концах отрезка принимает значение разных знаков , то существует С, С принадлежит [a,b] , такая что f(c) = 0.

Док-во

Пусть для определенности f(a) = A, f(b)=B , A<0, B<0.

Обозначим множество всех точек Х из [a,b] , в которых f(X) < 0

X не пусто и ограниченно =>

Докажем ,что f(c) = 0, для этого предположим противное. f(c) не равно нулю, то есть f(c)<0 либо f(c)>0. В первом случае по теореме о сохранении знака предела найдется окрестность точки «с» в которой f(х)<0 , то есть с

Во втором случае окрестность точки «с» в которой f(x)>0 , то есть sup надо уменьшить , что невозможно. В обоих случаях пришли к противному – теорема верна .

Теорема о промежуточном значении непрерывной функции.

Пусть f(x) непрерывна на [a,b] и принимает на концах отрезка неравные значения f(a)=A; f(b)=B.

Тогда для С расположенного между А и В С [a,b] , такое что f(c)=C.

Док-во

Пусть для определенности А<B , тогда A<C<B

Введем новую функцию : F(x)=f(x) – C, тогда F(a) = A- C<0; F(b)=B-C > 0, тогда по теореме об обращении непрерывной функции в ноль F(c) = 0 => f(c) =C – Теорема Доказана

Вопрос 15. Производная функции , ее геометрический и механический смысл. Уравнение касательной и нормали к линии . Представление функции в окрестности точки, в которой она имеет производную. Связь дифференцируемости с непрерывностью.

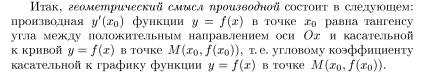
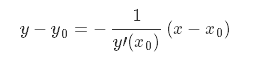Остальное от руки!

Вопрос 19 Обратная функция и ее производная . Производные обратных тригонометрических функций.

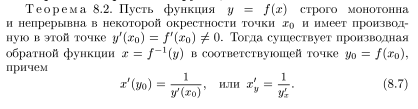
Вопрос 21. Производные и дифференциалы высших порядков.

Вопрос 23. Теорема Ролля. Теорема Лагранжа.

За

Замечание!

Из теорем Ролля и Лагранжа нельзя убрать ни одно из условий!

Вопрос 25. Формула Тейлора с остаточным членом в форме Пеано (с доказательством) и в форме Лагранжа ( без доказательства) .

В форме Лагранжа от руки!

Вопрос 27. Локальные экстремумы функции. Необходимое и достаточное условие.

Если дифференцируемая функция имеет во внутренней точке X₀ своей области определения локальный экстремум, то f’(X₀) = 0 => это необходимое условие экстремума . Итак , необходимым условием локального экстремума является равенство нулю производной или ее отсутствие. Точки, в которых производная равна нулю, называются стационарными точками функции. Точки в которых производная равна нулю или не существует называют критическими. Точки локального экстремума могут находиться только среди критических точек.

Теорема: Пусть f(x) определена и непрерывна в некоторой окрестности V(X₀) критической точки X₀ и дифференцируема по крайней мере в проколотой окрестности и сохраняет свой знак с каждой стороны окрестности, слева и справа от Х₀. Тогда, если f’(x) < 0 при X<X₀ и f’(X₀)>0 при X>X₀ , то в X₀- локальный минимум , а если f’(x)> 0 при X<X0 и f’(x)<0 при X>X₀ ,то максимум . Если знак производной не меняется, то локального экстремума нету. Замечание: в этой теореме находятся строгие локальные экстремумы. Достаточное условие строгого локального экстремума . Если первая производная при переходе через критическую точку меняет знак с + на - , то это max, с – на + , это min.