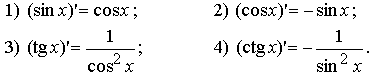Вопрос 2. Числовая последовательность. Предел последовательности. Свойства сходящихся последовательностей. Теорема о пределе монотонной ограниченной последовательности

Теоремы о последовательностях:

1. Если имеет предел, то он единственный.

2. Если сходящаяся, то она ограничена.

3. Если имеет предел а, имеет предел b и для любого n => а b (переход в пределе в неравенстве)

4. Если имеют общий предел А, а последовательность : , любое n, то существует (теорема о зажатой последовательности)

5. Сходимость монотонной ограниченной последовательности:

Монотонная ограниченная последовательность имеет предел

Доказательство:

Пусть последовательность не убывающая ( ) и существует М>0, |a_n|< M

Т.к. последовательность ограничена, то она имеет sup =b( точную верхнюю грань). Докажем, что b является пределом.

Возьмем любое >0. По определению точной верхней грани существует такой член последовательности (как множества)

Т.к. последовательность неубывающая, то для всех n>N, а_N ≤ a_n

Итак, => |а_n-b|<

Это означает, что

Вопрос 4. Бесконечно малые и бесконечно большие функции. Связь между ними.

Теорема о связи б.б. и б.м.

1)Пусть φ(х) б.б в точке X₀ R, тогда ψ(пси)(x) = - б.м. в точке X₀

=0

2) Пусть ψ(пси)(X) – б.М. В точке x0 r и окрестность точки х0 в которой ψ(х) 0, х х0,если x0 r.

Тогда в этой окрестности функция φ(х)= является бесконечно большой

=

Док-во

1. Берем , находим М = , так как φ(х) – б.б. в Х₀(пусть X₀ R) , то (М) , такое что при всех Х IX- X₀I< (М) , I φ(х)I > M=> φ(х)= < => = 0

Вопрос 6. Теорема о произведении бесконечно малой функции на ограниченную функцию. Ограниченные функции. Теорема об ограниченности функции, имеющей предел.

Вопрос 8. Теорема о пределе сложной функции. Теорема о пределе ”зажатой” функции. Предельный переход в неравенстве.

Предел зажатой функции

Предел зажатой функции

Если в некоторой окрестности точки Х₀ f₁(x) φ(х) f₂(x) и =b и =b, то =b

Теорема верна для X₀ R, b R

Док-во

Рассмотрим случай конечной Х₀ и b. По определению предела для взятого 0 ₁( ) и ₂( ), что для IX-X₀I < ₁( ) I f₁(x) – bI < и для IX-X₀I < ₂( ), I f₂(x) – bI <

Тогда для = min ( ₁( ), ₂( )) выполняется b- < f₁(x) f₂(x) < b+ => I -bI< =b

Вопрос 10. Предел функции при (без доказательства). Предел функции при . Следствия из второго замечательного предела.

Следствия!!

Следствия второго замечательного предела

1. =e , для = , (x) –б.б.

2. 

=(вводим y= -1, y+1= ,x=ln(y+1))= = = =1

3. Логарифмический предел.

=1

Биномиальный предел

=(( -1 = ; ( = +1; ln( +1)= ln(1+x)) - действительное число )= =1

Вопрос 12. Непрерывность функции в точке и на промежутке. Свойства

непрерывных функций. Односторонние пределы функции в точке.

Классификация точек разрыва функции. Примеры

Вопрос 14. Теорема о достижении непрерывной функцией, заданной на отрезке, своих наименьшего и не большего значений. Понятие равномерной непрерывности.

От руки!!

Вопрос 16. Правила дифференцирования. Производная сложной функции.

Дописать от руки!!

Вопрос 18. Производные тригонометрических функций.