2.1 Вариационные ряды

Пусть дана выборка наблюдений объема n

Вариационным рядом выборки называется такая последовательность наблюдений , в которой элементы упорядочиваются по возрастанию. Число , показывающее, сколько раз встречается значение в выборке, называется частотой i-го значения признака. Дискретным вариационным рядом называют расположенные в возрастающем порядке значения признака, указанные вместе с соответствующими частотами. Дискретный вариационный ряд представляют в виде таблицы.

Значение Признака	Количество наблюдений
z1 . . . zi . . . zk	n1 . . . ni . . . nk
Всего	n

Wi-относительная частота

Wi=ni/n

Интервальным вариационным рядом называют расположенные в возрастающем порядке границы интервалов группирования, указанные с соответствующими частотами.

Граница Интервала	Серед интерв	Кол-во наблюд
c0 - c1 c1 – c2 . . . ci-1 - ci . . . ck-1 - ck	z1 z2 . . . zi . . . zk	n1 n2 . . . ni . . . nk
Всего		n

Середина:

Накопленная частота:

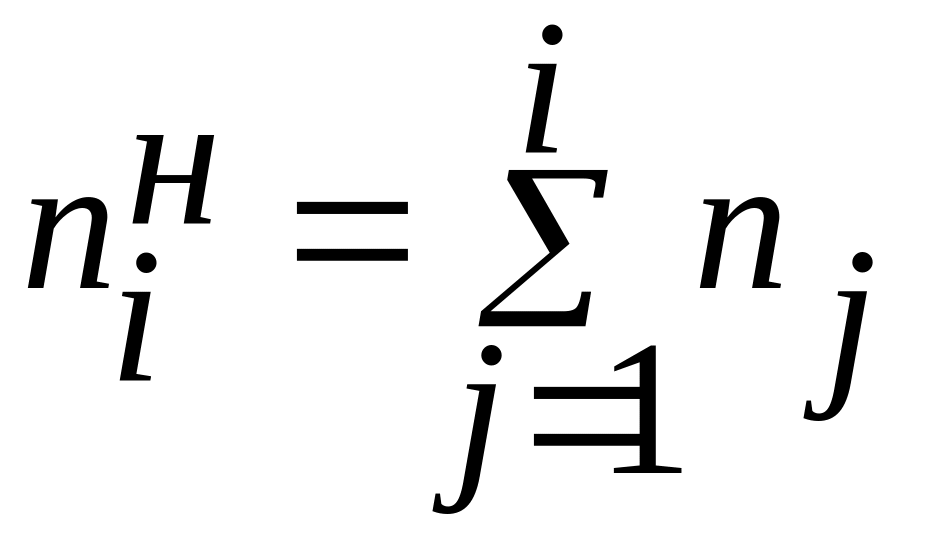
Относит. накопл. част.:

2.2 Основные выборочные числовые характеристики-это приближенные значения соответствующих числовых характеристик генеральной совокупности определяемые по выборочным значениям х1,…,хn

ДВР: Zi-i-ое наблюд. знач.

ni-кол-во набл zi

ИВР:Zi-середина i-го интервала группирования

-Выборочная мода – это такое значение признака которое наблюдается с большей частотой.

-Выборочная медиана-это серединное значение вариационного ряда.

3. Начальные и центральные моменты Вариац. Ряда.

Центральный момент m-го порядка:

Начальный момент:

4.Графическое представление вариационного ряда.

Графические изображения вариационных рядов:

-полигон частот;

-гистограмма;

-график эмпирической функции распределения.

a) Полигон частот служит для изображения дискретного вариационного ряда. Для построения полигона в прямоугольной системе координат наносят точки с координатами , затем соседние точки соединяют отрезками прямых. В результате получают ломаную линию.

b) Гистограмма служит для изображения интервального вариационного ряда. Для ее построения в прямоугольной системе координат по оси абсцисс откладывают отрезки, изображающие интервалы, и на этих отрезках как на основании строят прямоугольники с высотами, равными частотам соответствующего интервала (абсолютным или относительным). В результате получается ступенчатая фигура, состоящая из прямоугольников и называемая гистограммой.

c) График эмпирической функции распределения для дискретного вариационного ряда представляет собой кусочно-постоянную функцию, по аналогии с функцией распределения дискретной случайной величины. График имеет скачки в точках , соответствующих наблюдаемым значениям признака.

При построении графика функции для интервального вариационного ряда наносят точки с координатами , то есть по оси абсцисс откладывают правую границу интервала, а по оси ординат относительную накопленную частоту интервала.

(ломаная прямая )