9.1 Случайные величины

Типы.

Случайной наз. величина кот. в результате испытания принимает одно и только одно возможное значение наперед известное и зависящее от случ. причин кот. заранее не могут быть учтены.

Случ. величина Х – это числовая ф-ция, заданная на пространстве элемент. событий

ТИПЫ

1) Непрерывные

2) Дискретные:

-принимают 1 из множества различных значений с вер. появления какого-либо одного значения больше 0.

х1,х2,…,хn

Р(хi)>0 i=1,2,3

9.2 Закон распр. Вероятн. Д.С.В. Многоуг. Распр.

xi, i=1,…,n, P(X=xi)

Законом распр. дискр. случ. величины наз. соответствие между возможными значениями и их вероятностями.

Способы задания:

1)Табличный:

х	х1	х2	хi	хn
P	P1	P2	Pi	Pn

Х=хi X=xj i,j= 1,…,n i j

2) Формула бином. распр.

3)Графический(многоуг)

(xi;pi)

Р

x

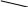
10. Гипергеометрическое распределение

Дано N деталей, бракованные n, выбрали M

Найти вер. того, что среди выбр. дет. М, m- брак.

n N , M N, n=0,1,…,min

стандартн. детали. N-n, M-m

X-кол-во брак. дет. среди М выбр.

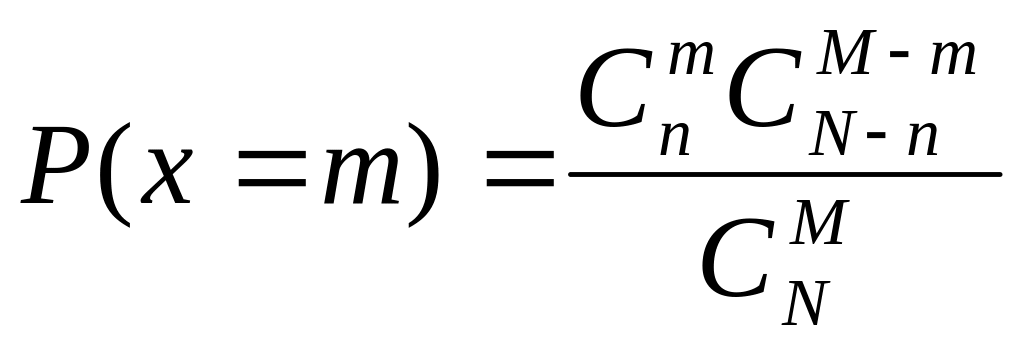
11. Геометрическое распределение

Испытания проводят до первого появления события А

Х-кол-во провед. испыт.

х-1,2,3,…,к,…

Р(х=к)= -геометрическая прогр.

12. Биноминальное распределение.

Формула бином. распр.

х-кол-во появлений событий А в n испытаниях

х-1,2,3,…,к,…n

13. Распределение Пуассона.

Когда n велико, Р мала ,а

произведение np=

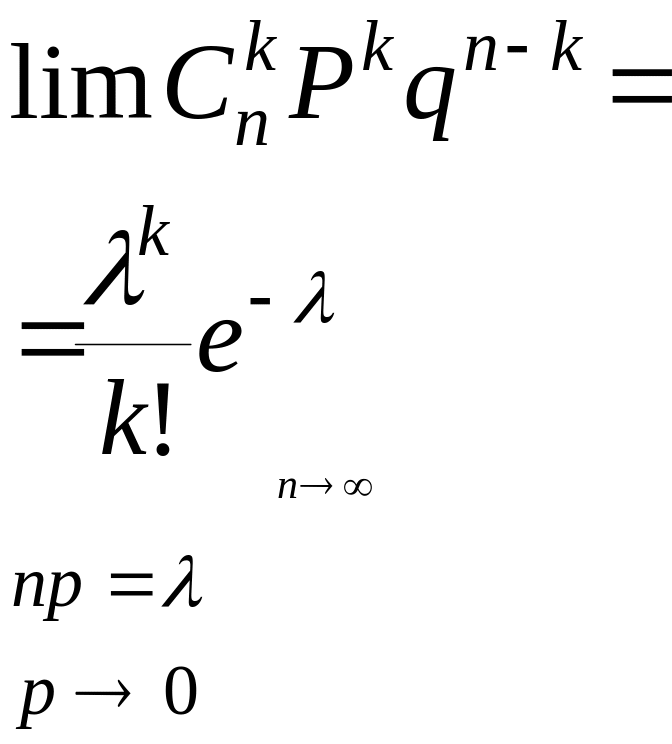
,где К не более 5

Х- кол-во появлений успехов

К=0,1,2,3,..

14. Математические операции над случайными величинами

Две случайные величины наз. независимыми, если закон распределения одной из них не меняется от того какие возможные значения приняла другая величина.

Х	Х1	Х2	…	Хn
Y	Y1	Y2	…	Yn

Если Х и Y независ., то

Х=хi, i=1,n

Y=yj, j=1,…,m

1. Случ. величена Кх=кх, i=1,…,n

2. наз. случ. велич. 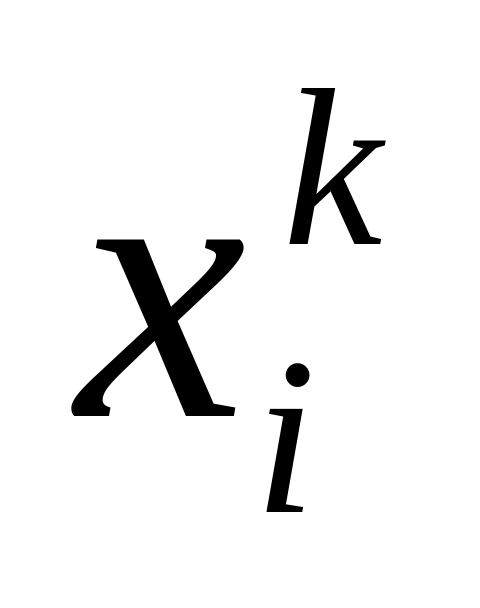, i=1,…,n , с вероятн. pi

3. Суммой (разностью/произведением) случайных величин Х и Y наз. случ. величину Z (Z=X+Y)((Z=X-Y;Z=XY)), кот. принимает все значения

Zj=Xi+Yj

i=1,…,n

j=1,…,m

Pij=P(X=xi;Y=yj)

Если X и Y независ., то Pij=PiPj